How to Use Fractions in Chemistry
TLDRThe video script provides a comprehensive guide on mastering fractions, which are crucial for understanding various chemistry topics. It begins by explaining the basic components of a fraction and then delves into how to multiply fractions, emphasizing the importance of simplifying the result. The script also covers multiplying whole numbers by fractions, which involves converting the whole number into a fraction. A significant portion of the script is dedicated to balancing chemical equations, explaining the process of ensuring equal elements on both sides of the equation and the strategy of addressing hydrogen and oxygen last due to their frequent occurrence. The video further explains how to divide fractions by using reciprocals and the application of this skill in chemistry, particularly in kinetics. Adding and subtracting fractions are also discussed, with a focus on finding a common denominator. The script concludes with an application of these skills in Hess's law, which is used to calculate the change in enthalpy of a reaction by combining multiple chemical equations. The summary also highlights three key rules for manipulating chemical equations in Hess's law and provides a step-by-step example to illustrate the process. The video aims to equip viewers with the mathematical skills necessary for advanced chemistry concepts.
Takeaways
- 🧮 **Fraction Mastery**: Understanding fractions is crucial for chemistry, especially in balancing chemical equations and related calculations.
- 📚 **Fraction Components**: A fraction has a numerator (top number) and a denominator (bottom number), which are essential for arithmetic operations.
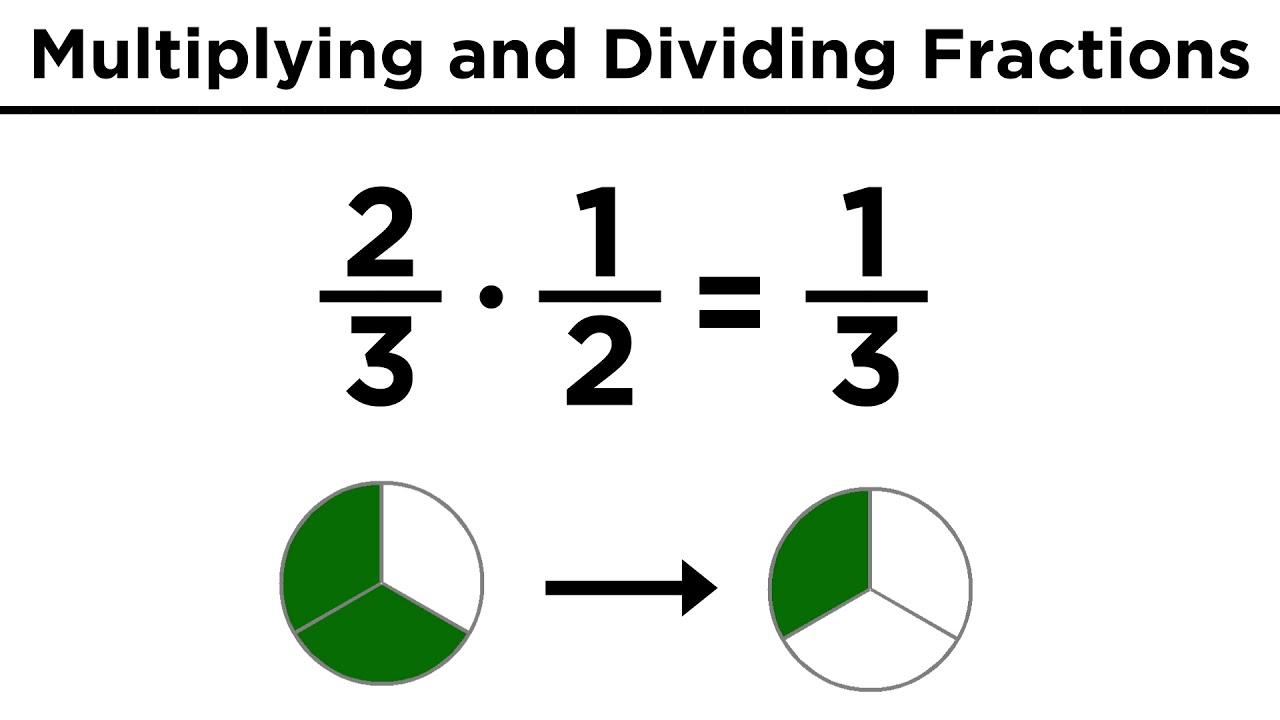
- ✖️ **Multiplying Fractions**: To multiply fractions, simply multiply the numerators together and the denominators together without needing a common denominator.
- 🔄 **Simplifying Fractions**: After multiplication, fractions should be simplified by dividing both the numerator and the denominator by their greatest common divisor.
- 🧫 **Chemical Equation Balancing**: In chemistry, balancing equations involves ensuring equal numbers of each element on both sides of the equation.
- 🔢 **Coefficient Placement**: When balancing equations, coefficients (multipliers) must be placed in front of the entire compound or molecule, not within it.
- 💧 **Balancing Hydrogen and Oxygen**: Tend to balance hydrogen and oxygen last, especially oxygen, as it often appears in multiple locations within a chemical equation.
- 🔴 **Balancing with Fractions**: If whole number coefficients don't suffice, fractions can be used to balance the number of atoms of an element.
- 🔁 **Reciprocals in Division**: Dividing fractions is achieved by multiplying by the reciprocal of the second fraction, which involves flipping the second fraction.
- ➗ **Units in Chemistry**: Knowledge of fraction division is important for determining units in chemistry, such as in kinetics for rate constants.
- ↔️ **Adding and Subtracting Fractions**: For addition and subtraction, fractions must have a common denominator. The least common multiple (LCM) is used to find this common denominator.
- 🔥 **Hess's Law**: Hess's law is used to calculate the enthalpy change of a reaction by combining multiple chemical equations to match a 'goal' reaction.
- ⚖️ **Enthalpy Rules**: When manipulating chemical equations, remember to reverse the sign of enthalpy change when flipping reactions and multiply the enthalpy by the same number used to scale the equation.
- 📉 **Combining Equations**: Add up all adjusted and unadjusted chemical equations to get the final goal reaction, ensuring all reactants and products are correctly matched.
Q & A
What is the first step in multiplying two fractions?
-The first step in multiplying two fractions is to multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator.
How can you simplify a fraction after multiplication?
-To simplify a fraction after multiplication, look for common factors in both the numerator and the denominator and divide by the greatest common divisor.
What is the process of turning a whole number into a fraction when multiplying with a fraction?
-When multiplying a whole number with a fraction, you can turn the whole number into a fraction by placing a 1 as the denominator.
Why is it recommended to balance carbons first when balancing a chemical equation?
-It is recommended to balance carbons first because they often form the backbone of organic compounds, and balancing them early can make the process of balancing other elements more straightforward.
How do you find the common denominator for adding and subtracting fractions?
-To find the common denominator for adding and subtracting fractions, you need to determine the least common multiple (LCM) of the two denominators.
What is the purpose of balancing a chemical equation?
-The purpose of balancing a chemical equation is to ensure that the number of atoms for each element is the same on both sides of the equation, adhering to the law of conservation of mass.
What is the reciprocal of a fraction and how is it used in division?
-The reciprocal of a fraction is obtained by swapping the numerator and the denominator. It is used in division by multiplying the first fraction by the reciprocal of the second fraction, effectively changing the division operation to multiplication.
How does the concept of enthalpy relate to Hess's law?
-Enthalpy is the heat absorbed or released by the system, and Hess's law is used to calculate the total enthalpy change of a reaction by combining multiple chemical equations that lead to the same final products and reactants.
What are the three rules to remember when manipulating and combining chemical equations according to Hess's law?
-The three rules are: 1) If you reverse a reaction, multiply the enthalpy change by -1. 2) If you multiply an entire chemical equation by a number, multiply the enthalpy change by that number. 3) Add all the chemical equations and their enthalpy changes to get the overall enthalpy change of the reaction.
Why is it important to cancel out like terms on opposite sides of the arrows in a chemical equation?
-Canceling out like terms on opposite sides of the arrows ensures that the final equation represents the net chemical change that occurs and helps in achieving the goal reaction.
How can you determine if a chemical equation is balanced correctly?
-A chemical equation is balanced correctly when the number of atoms for each element is the same on both sides of the equation, and the equation represents the actual chemical process taking place.
What is the significance of the fraction 13 halves in the context of balancing chemical equations?
-The fraction 13 halves is used to balance the number of oxygen atoms on the product side of the equation when no whole number can achieve the required balance.
Outlines
🧮 Fractions in Chemistry
This paragraph introduces the importance of understanding fractions for chemistry, particularly in balancing chemical equations. It explains the basic components of a fraction, numerator and denominator, and demonstrates how to multiply fractions without needing a common denominator. The process of simplifying fractions and multiplying whole numbers with fractions is also covered. The video uses an example of balancing a chemical equation to illustrate these concepts, emphasizing the need to balance elements and the common practice of balancing carbons and hydrogens before oxygens.
🔄 Balancing Equations and Fractions
The second paragraph delves into the process of balancing chemical equations, starting with carbon and then moving on to hydrogen and oxygen. It explains the method of using fractions to balance elements that do not have a whole number coefficient, by finding a fraction that equals the desired number of atoms and then multiplying the entire equation by the denominator of that fraction to clear the fractions. The paragraph also transitions into dividing fractions, introducing the concept of reciprocals and how to use them in division, which is particularly useful in chemistry for finding units in kinetics problems.
⚖️ Adding and Subtracting Fractions, Hess's Law
The third paragraph focuses on adding and subtracting fractions, which requires a common denominator. It explains how to find the least common multiple to create a common denominator and then combine the numerators while keeping the denominator constant. The paragraph also touches on the application of these skills in Hess's law, which is used to calculate the change in enthalpy of a reaction by combining multiple chemical equations. It outlines three rules for manipulating chemical equations and provides a step-by-step example of how to apply these rules to find the enthalpy change of a given reaction.
Mindmap
Keywords
💡Fractions
💡Numerator
💡Denominator
💡Chemical Equations
💡Balancing
💡Reciprocal
💡Least Common Multiple (LCM)
💡Hess's Law
💡Enthalpy
💡Kinetics
💡Stoichiometry
Highlights
Four out of three students struggle with fractions, emphasizing the common difficulty in understanding them.
Properly performing arithmetic operations with fractions is crucial for grasping major chemistry topics.
A fraction's numerator is the top number, and the denominator is the bottom number.
When multiplying fractions, there's no need for a common denominator; simply multiply straight across.
Simplification of fractions involves dividing both the numerator and denominator by the same number.
Cancelling out common factors in fractions simplifies the calculation process.
Whole numbers can be treated as fractions with a denominator of one for multiplication with fractions.
Balancing chemical equations involves ensuring equal numbers of each element on both sides.
Oxygen is often left until last in balancing chemical equations due to its frequent appearance in different forms.
Balancing carbons in chemical equations by adjusting coefficients without breaking molecules.
Hydrogen and oxygen are typically balanced last in chemical equations due to their common presence in compounds.
Fractions are used to balance elements that cannot be evenly divided by whole numbers in chemical equations.
The reciprocal of a fraction is used when dividing fractions, effectively turning division into multiplication.
Finding the proper units in chemistry problems, such as kinetics, often involves dividing fractions.
Like terms in fraction division can be cancelled out to simplify the expression.
A common denominator is necessary for adding and subtracting fractions, derived from the least common multiple.
Hess's law is used to find the change in enthalpy of a reaction by combining multiple chemical equations.
Three specific rules apply when manipulating and combining chemical equations for Hess's law calculations.
The goal of Hess's law problems is to manipulate given equations to match a 'goal reaction'.
Changing or not changing chemical equations and combining their enthalpy changes gives the overall enthalpy for the reaction.
Transcripts
Browse More Related Video

Balancing Chemical Equations With Fractions | How to Pass Chemistry
Multiplication and Division of Fractions

Multiplying and Dividing Fractions | A Complete Guide | Math with Mr. J

Balancing chemical equations | Chemical reactions | High school chemistry | Khan Academy

Balancing Chemical Equations

Balancing Chemical Equations With Polyatomic Ions and Fractions | Study Chemistry With Us
5.0 / 5 (0 votes)
Thanks for rating: