3/2(x + 4) = 5 – 1/3(4 – x), many don’t know the EASY way to solve!
TLDRIn this instructional video, math teacher John tackles solving linear equations with fractions, emphasizing the importance of a step-by-step approach to avoid errors. He presents two methods: the conventional, more laborious technique involving fraction manipulation, and a simpler strategy using the lowest common denominator (LCD) to eliminate fractions early in the process. John's clear explanation and practical tips aim to demystify algebra for learners, encouraging persistence and highlighting the value of practice in mastering mathematical concepts.
Takeaways
- 📚 The primary goal when solving a linear equation is to isolate the variable (X).
- 💡 Students often choose a more complicated method to solve equations involving fractions, but there are easier approaches.
- 👨🏫 The speaker, John, has decades of experience teaching math and aims to make learning math easier.
- 🎓 John suggests using the distributive property when dealing with parentheses in an equation.
- 🔢 It's crucial to perform fraction operations correctly, as errors can lead to incorrect solutions.
- 🤔 Before solving, find the lowest common denominator (LCD) to simplify fractions in the equation.
- 📈 When solving equations, it's beneficial to keep track of each step to catch and correct any potential errors.
- 🎯 The hard way to solve the equation involves extensive work with fractions and can be time-consuming.
- 🚀 John emphasizes the importance of practicing and learning from experience to improve math skills.
- 📊 To clear fractions from an equation, multiply both sides by the LCD, which simplifies the process.
- 🌟 The speaker encourages viewers to subscribe and use his resources for better math understanding and practice.
Q & A
What is the main objective of the video?
-The main objective of the video is to demonstrate how to solve a linear equation with fractions, showcasing both a harder method and an easier approach.
What is the correct answer to the equation presented in the video?
-The correct answer to the equation is X equals negative two.
How does John, the instructor, introduce himself in the video?
-John introduces himself as a teacher with decades of experience in teaching middle and high school math, passionate about making learning math as easy as possible.
What is the golden rule of algebra mentioned in the video?
-The golden rule of algebra mentioned is that whatever you do to one side of the equation, as long as you do it equally to the other side, you are allowed to do that operation.
What is the importance of finding the lowest common denominator (LCD) in solving the equation?
-Finding the LCD is important because it allows you to clear away fractions in one move, simplifying the equation and making it easier to solve.
What is the easier approach to solving the equation with fractions that John suggests?
-The easier approach John suggests is to multiply the entire equation by the lowest common denominator (LCD) to eliminate fractions before solving the equation.
How does John emphasize the importance of practice in learning mathematics?
-John emphasizes that practice is crucial in learning mathematics, as it helps to reinforce understanding and improve problem-solving skills. He advises practicing with a variety of problems, starting with easier ones and gradually moving to more challenging ones.
What is the significance of the distributive property in solving the equation?
-The distributive property is significant in solving the equation as it allows you to multiply a number outside of parentheses to each term inside the parentheses, simplifying the equation and making further calculations easier.
What is the final result after simplifying the equation using the easier method?
-After simplifying the equation using the easier method, the final result is 7x plus 36 equals 22, which simplifies further to 7x equals negative 14, and ultimately x equals negative 2.
How does John address the common frustration students feel with fractions?
-John acknowledges that students often dislike dealing with fractions and finds it challenging. He encourages students to persist, offering reassurance that with practice and the right techniques, they can overcome this challenge and improve their math skills.
What advice does John give to students to avoid making errors in algebra?
-John advises students to be neat, organized, structured, and to take their time when solving problems. He also emphasizes the importance of checking your work as you go to catch any errors early, which can save time and prevent incorrect results.
Outlines
📘 Introduction to Solving Linear Equations with Fractions
The speaker, John, introduces the topic of solving linear equations with fractions. He emphasizes that while the problem at hand can be solved easily, most students tend to choose a more difficult approach. John, an experienced math teacher, encourages viewers to attempt the problem and share their answers in the comments. He promises to reveal the correct answer, which is X = -2, and to demonstrate both the hard and easier methods for solving the equation. John also promotes his math help program and stresses the importance of checking one's work to avoid errors in multi-step problems.
📗 The Hard Way: Using Distributive Property and Fractions
John begins by explaining the hard way to solve the equation, which involves using the distributive property to deal with the fractions. He details the process of multiplying fractions and combining like terms. John shows the steps of moving terms around the equation and emphasizes the importance of neat and organized work to prevent errors. He also discusses the need to find a common denominator when subtracting fractions and illustrates how to perform this operation. However, he acknowledges that this method is time-consuming and error-prone due to the extensive work with fractions.
📙 The Easier Approach: Clearing Fractions with LCD
John introduces an easier method for solving equations with fractions by clearing them away in one move using the lowest common denominator (LCD). He explains the process of finding the LCD for all fractions in the equation and multiplying the entire equation by this value. This approach significantly reduces the fraction work and simplifies the equation. John demonstrates how to use the distributive property after clearing fractions and how to rearrange the terms to isolate the variable X. He emphasizes that this method is more efficient and less prone to mistakes than the hard way.
📕 The Importance of Practice and Good Instruction
In the final paragraph, John stresses the importance of good instruction and practice in mastering algebra and mathematics. He advises viewers to seek clear and comprehensive instruction and to practice regularly with a variety of problems. John dispels the notion of shortcuts in learning math and encourages perseverance and consistent effort. He concludes by wishing viewers well in their mathematical endeavors and thanks them for their time and attention.
Mindmap
Keywords
💡Linear Equation
💡Fractions
💡Distributive Property
💡Solving for Variable
💡Algebra
💡Mathematics Teaching
💡Step-by-step
💡LCD (Lowest Common Denominator)
💡Practice
💡Math Help Program
Highlights
The objective of the transcript is to solve a linear equation with fractions, emphasizing the importance of finding the variable X.
The speaker, John, introduces himself as a math teacher with decades of experience, passionate about making math learning as easy as possible.
John mentions his math help program at tcmathacademy.com for those needing assistance in mathematics.
The correct answer to the equation is X equals negative two, which is a significant accomplishment for those who solve it.
John emphasizes the importance of solving equations step by step and checking your work to avoid mistakes.
The transcript explains the process of solving a linear equation with fractions using the hard way and then the easier approach.
The hard way involves using the distributive property and dealing with fractions, which can be challenging.
John provides a detailed explanation of how to use the distributive property with fractions, including finding a common denominator.
The transcript highlights the importance of being neat, organized, and taking your time when solving complex math problems.
John explains how to clear fractions away in one move by using the lowest common denominator (LCD) of all fractions in the equation.
The easier approach to solving the equation involves multiplying both sides of the equation by the LCD to eliminate fractions.
John provides a step-by-step guide on how to simplify the equation by using the LCD and the distributive property.
The transcript emphasizes the value of practice in improving algebra and math skills, and the importance of not taking shortcuts.
John encourages viewers to subscribe to his YouTube channel for more math content and resources.
The transcript concludes with a message of encouragement for those on their mathematics journey, emphasizing the importance of perseverance and practice.
Transcripts
Browse More Related Video
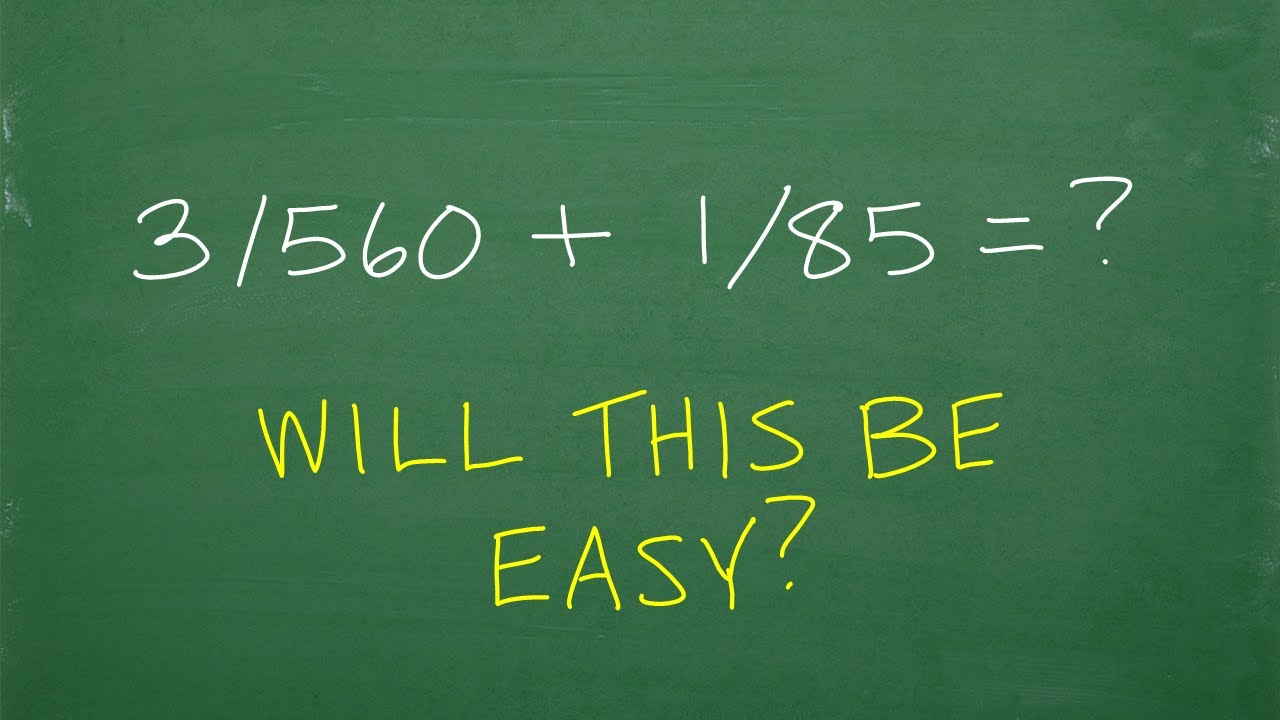
3/560 + 1/85, will this be EASY?
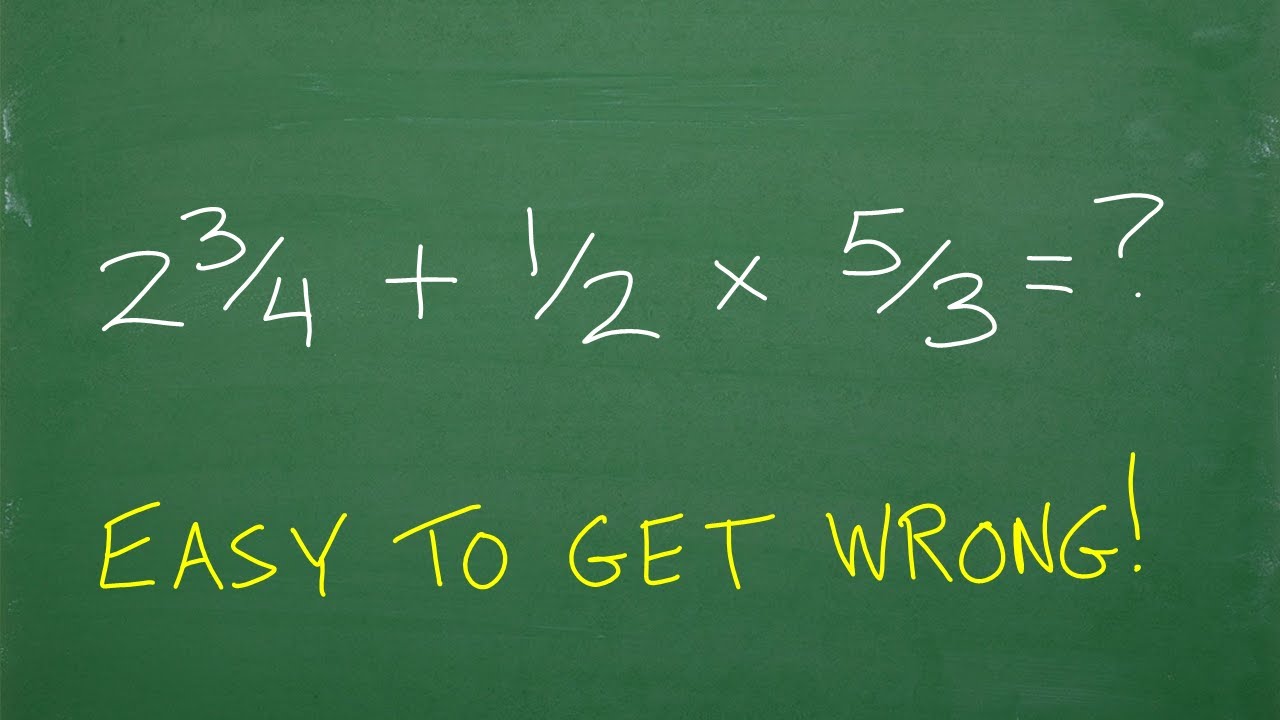
(2 and 3/4) plus 1/2 times 5/3 = ? What’s the first thing you should be thinking in this problem?

Fractions Made EASY!
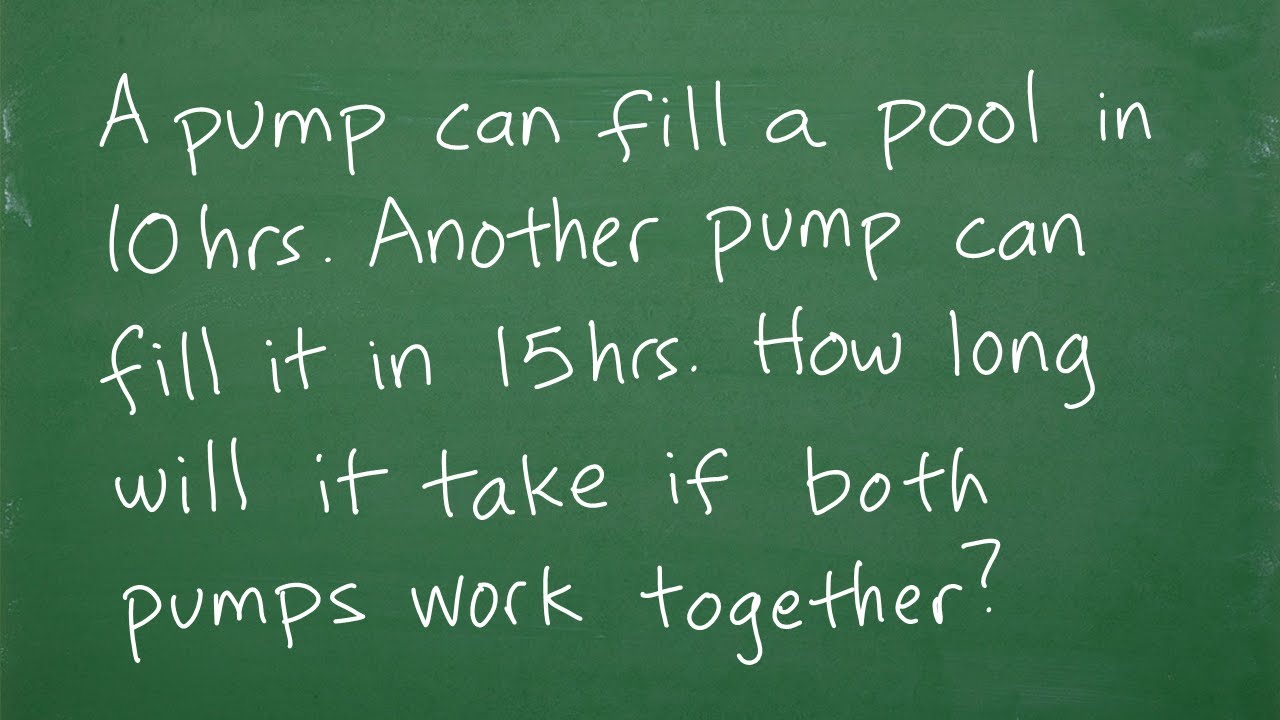
A pump can fill a pool in 10hrs. Another pump can fill it in 15hrs. Both pumps together will take?

Quadratic Formula – MOST COMMON MISTAKES!
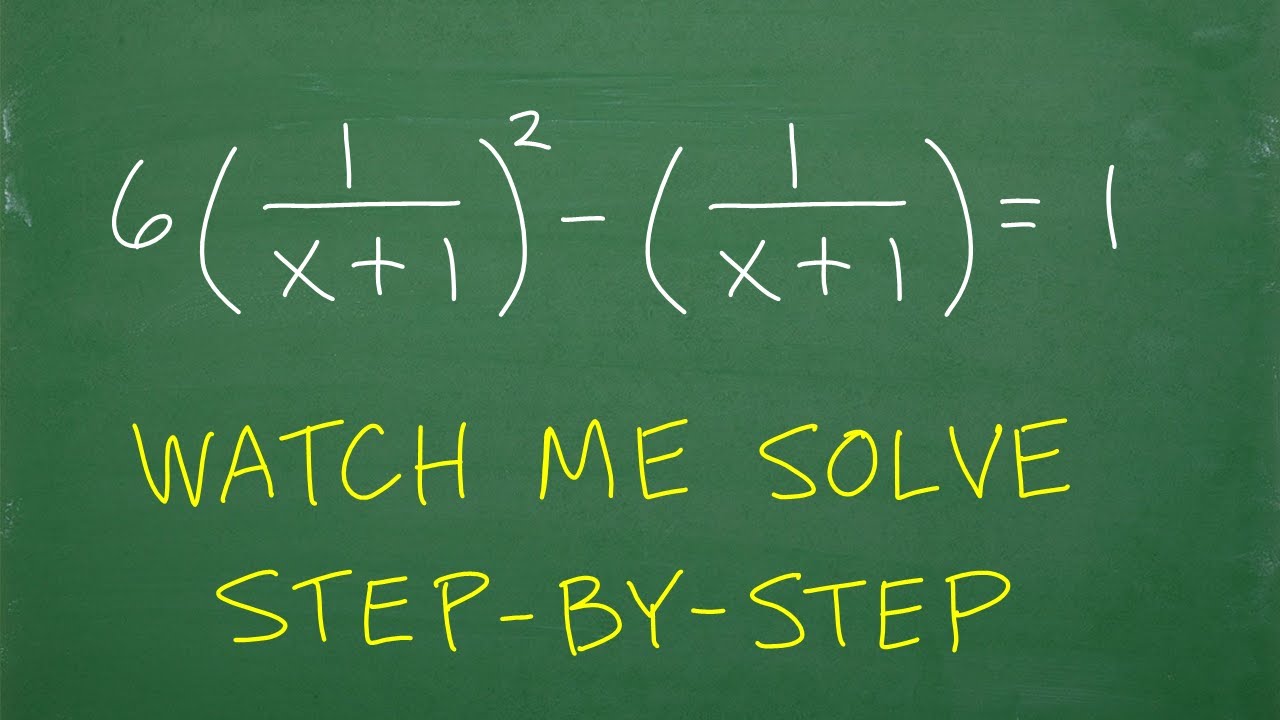
Watch me solve this Rational Equation – step-by-step
5.0 / 5 (0 votes)
Thanks for rating: