Lesson 07: Abstracting the Derivative Slopes
TLDRThis lecture explores the concept of derivatives in various contexts, starting with a geometric interpretation as the slope of a tangent line on a graph. It delves into the algebraic computation of derivatives from algebraic expressions of functions. The instructor then discusses applications of derivatives in different geometric settings, such as the rate of change of a square's area with respect to its side length, the volume growth of a cube, and the area change of a circle as its radius varies. The lecture also covers the surprising effect of increasing the Earth's belt size and the growth rate of stalactites, illustrating the practical implications of derivatives in understanding change and rate in diverse scenarios.
Takeaways
- 📚 The script discusses the concept of derivatives in various contexts, emphasizing their importance in understanding changes and dependencies in mathematical functions.
- 📈 It explains the geometric interpretation of derivatives, starting with the derivative of x squared, which represents the slope of the tangent line to the curve at any point x.
- 🔶 The lecture uses the area of a square as an example to illustrate the derivative's geometric meaning, showing that the rate of area increase is proportional to the side length of the square.
- 📊 The script moves on to the volume of a cube, explaining how the derivative of x cubed (3x squared) can be visualized as the rate at which the volume of the cube increases as its sides grow.
- ⭕ It also covers the area of a circle, using pi r squared as the formula, and explains the derivative in terms of the rate of area change with respect to changes in the radius.
- 🌐 An interesting example is given about the Earth's equator, where adding a small length to the circumference results in a larger increase in radius, challenging common intuition.
- 🏞 The growth of stalactites in caves is used as an analogy to discuss how the derivative can represent the rate of change in weight or volume over time, with a cone-shaped stalactite as an example.
- 📉 The script touches on economic principles, specifically supply and demand curves, and how the derivatives (slopes) of these curves can indicate the elasticity of a good in the market.
- 📚 The power of derivatives is highlighted in understanding not just algebraic expressions but also their applications in real-world scenarios, from geometry to economics.
- 🔑 The importance of the derivative is underscored as a tool for analyzing rates of change in various contexts, such as the growth of geometric shapes or economic models.
- 👋 The lecturer concludes by mentioning the next lecture's focus on ancient developments that were precursors to the integral, indicating a continuation of the exploration of calculus concepts.
Q & A
What is the geometric interpretation of the derivative of x squared?
-The derivative of x squared, which is 2x, geometrically represents the slope of the tangent line to the graph of x squared at any point x. It can also be interpreted as the rate at which the area of a square with side length x is increasing as the side length changes.
How does the lecture relate the derivative of a function to the rate of change of a circle's area with respect to its radius?
-The lecture explains that the derivative of the area formula for a circle (pi * r^2) with respect to its radius r is 2 * pi * r. This derivative indicates the rate at which the area of the circle increases as the radius changes.
What is the significance of the derivative of x cubed in the context of a growing cube?
-The derivative of x cubed, which is 3x squared, signifies the rate at which the volume of a cube with side length x is increasing as the side length changes. It can be visualized as the volume added on three faces of the cube as it grows.
How does the lecture use the concept of derivatives to analyze the growth of stalactites?
-The lecture uses the derivative of the weight function of a stalactite, which is proportional to its volume, to determine the rate at which the stalactite's weight increases over time. It shows that the rate of weight gain is higher for older stalactites due to the larger volume of material added per unit increase in height.
What economic concept is related to the derivatives of supply and demand curves?
-The lecture relates the derivatives of supply and demand curves to the concept of elasticity in economics. A good with sharply crossing supply and demand curves and steep derivatives is considered elastic, meaning its price tends to be stable. In contrast, a good with almost tangent supply and demand curves is inelastic, indicating a large range of price variation.
How does the lecture demonstrate the geometric interpretation of the derivative of the area of a circle?
-The lecture demonstrates this by considering a circle with radius r and then increasing the radius by Δr to create an annulus. The additional area of this annulus, when divided by Δr, approaches 2 * pi * r as Δr goes to zero, which is the derivative of the area function.
What is the relationship between the derivative of a function and the concept of a tangent line?
-The derivative of a function at a given point is the slope of the tangent line to the graph of the function at that point. It measures the rate of change of the function, which geometrically is the steepness of the tangent line.
How does the lecture illustrate the concept of derivatives using the example of a growing square?
-The lecture illustrates this by considering a square with side length x and then imagining a larger square with side length x + Δx. The additional area created by this increase in side length, when divided by Δx, approaches 2x as Δx goes to zero, which is the derivative of the area function for a square.
What is the formula for the volume of a cone, and how is it related to the derivative?
-The volume of a cone is given by (1/3) * π * r^2 * h, where r is the radius and h is the height. The derivative of this volume function with respect to time can be used to analyze the rate at which the volume (and thus the weight, assuming constant density) of a stalactite is increasing.
How does the lecture use the concept of derivatives to analyze the Earth's equator with a belt?
-The lecture uses the formula for the circumference of a circle (2 * π * r) and its derivative (2 * π) to analyze how increasing the belt's length by a small amount (7 feet) results in a larger increase in the radius, making the belt more than a foot off the ground everywhere on the equator.
Outlines
📚 Introduction to Derivatives and Their Applications
This paragraph introduces a series of lectures on the concept of derivatives, starting with a geometric interpretation as the slope of the tangent line to a curve at any given point. It then transitions into an algebraic understanding, explaining how to compute derivatives from algebraic expressions of functions. The lecturer emphasizes the broader applications of derivatives beyond change over time, such as in relationships where one quantity depends on another, exemplified by the area of a circle dependent on its radius. The session aims to explore various applications of derivatives, starting with geometric manifestations and moving towards more abstract concepts.
📐 Geometric Interpretation of Derivatives: The Square and Its Area
The lecturer delves into the geometric interpretation of derivatives using the example of a square. They remind the audience of the derivative formula for x squared, which equals 2x, and explain that this represents the slope of the tangent line at any point on the graph of x squared. The geometric implication is that constructing a square with side length x results in an area of x squared. The derivative's role in understanding how the area of the square changes with respect to changes in its side length is explored, demonstrating that the rate of change of the area can be visualized as the sum of the lengths of two sides of the square multiplied by an infinitesimally small change in the side length (Delta X).
📏 Derivatives and the Growth of Geometric Shapes: Cubes and Volume
This paragraph continues the geometric theme by examining the derivative of x cubed, which represents the volume of a cube with side length x. The lecturer explains that the derivative of x cubed is 3x squared, which geometrically means that as a cube grows, the rate of increase in volume is associated with the areas of three faces of the cube, each with an area of x squared. The example illustrates that the volume's rate of increase can be understood by considering the additional material added to the three faces of the cube as it grows, leading to the conclusion that the derivative corresponds to the rate at which the cube's volume is expanding.
🌐 The Derivative of a Circle's Area and Its Radius
The lecturer shifts focus to the area of a circle, which is given by the formula pi times the radius squared (pi r squared). They explain the algebraic derivative of this area formula, which results in 2 pi times the radius (2 pi r). Geometrically, this means that for a unit increase in the radius, the area of the circle increases by 2 pi times the radius. The concept is visualized by considering an annulus formed by increasing the radius by Delta r and approximating the additional area by considering the annulus as a belt around the circle. The derivative, in this case, represents the rate at which the area of the circle grows per unit increase in the radius.
🌎 Derivatives in Real-World Applications: Earth's Circumference and a Belt
This paragraph presents a real-world application of derivatives by considering the Earth's equator and a belt that fits exactly around it. The lecturer poses a thought experiment where the belt is loosened by adding seven feet to its length, leading to a new question about how far off the ground the belt would be. The explanation uses the derivative of the circumference of a circle with respect to its radius, which is 2 pi, to show that the belt would be more than a foot off the ground everywhere, contrary to common intuition. This example demonstrates the practical implications of derivatives in understanding changes in physical dimensions.
🏞️ Growth Dynamics of a Stalactite: Volume and Weight
The lecturer explores the growth of a stalactite in a cave, using a conical model where the stalactite maintains a constant shape as it grows, with the height being three times the age in thousands of years and the radius being one-sixth of the height. They provide a formula for the weight of the stalactite, which is proportional to its volume, and discuss the rate of change of this weight over time. The derivative of the weight function is computed to show that the rate of weight increase is greater at 20,000 years than at 10,000 years, illustrating the concept that as the stalactite grows larger, the same increase in height results in a greater increase in weight.
📈 Economic Implications of Derivatives: Supply, Demand, and Elasticity
In the final paragraph, the lecturer applies the concept of derivatives to economic scenarios involving supply and demand curves. They explain that the sharpness of the intersection of these curves indicates the elasticity of a good. A good with elastic demand will have stable prices due to a greater imbalance resulting from any deviation from the equilibrium price. Conversely, an inelastic good, such as gasoline, has a demand that remains relatively constant over a wide range of prices, leading to larger variations in price. This example ties the mathematical concept of derivatives to economic theory, showing how the slopes of functions can inform real-world economic behavior.
Mindmap
Keywords
💡Derivative
💡Geometric Interpretation
💡Algebraic Expression
💡Rate of Change
💡Tangent Line
💡Limit
💡Area Function
💡Volume Function
💡Supply and Demand
💡Elasticity
Highlights
Introduction to the concept of derivatives and their geometric interpretation.
Explanation of the derivative as the slope of the tangent line to a curve at any given point.
Algebraic computation of derivatives from a function's expression.
Derivatives' applications in understanding changes over time, such as a car's movement.
Use of derivatives to analyze dependencies between quantities, such as the area of a circle relative to its radius.
Derivative of x squared (2x) and its geometric interpretation involving the area of a square.
Geometric procedure to understand the derivative of a square's area as it grows.
Derivative of x cubed (3x squared) and its geometric interpretation with the volume of a cube.
Visual representation of the rate at which a cube's volume increases.
Derivative of the area of a circle formula (pi r squared) and its geometric meaning.
Geometric interpretation of the derivative showing the rate of area increase in a circle.
The surprising result of adding length to a belt around the Earth and its relation to the derivative.
Derivative's role in understanding the relationship between the Earth's radius and its circumference.
Growth of a stalactite in a cave as a physical phenomenon explained using derivatives.
Derivative's application in determining the rate of weight increase of a stalactite over time.
Economic analysis using derivatives to understand supply and demand curves.
Differentiation between elastic and inelastic goods using the concept of derivatives.
Anticipation of the next lecture's topic on ancient developments related to the integral.
Transcripts
Browse More Related Video

Lecture 05: Visualizing the Derivative Slopes

Lec 2 | MIT 18.01 Single Variable Calculus, Fall 2007
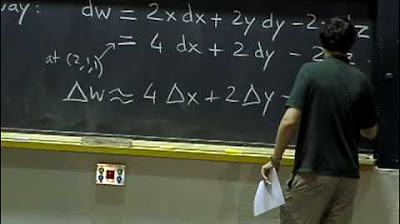
Lec 12: Gradient; directional derivative; tangent plane | MIT 18.02 Multivariable Calculus, Fall 07

Math 11 - Sections 1.3-1.4

Math Calculus for Business and Economics - Related Rates wrt time Episode. 1 LIVE MATH

Calculus 1 Lecture 2.1: Introduction to the Derivative of a Function
5.0 / 5 (0 votes)
Thanks for rating: