Math Calculus for Business and Economics - Related Rates wrt time Episode. 1 LIVE MATH
TLDRThe transcript appears to be a detailed lecture on calculus, specifically focusing on derivatives and their applications. The lecturer begins by reviewing the concept of a derivative as a rate of change, differentiating between dy/dx and the actual change dy, and introduces the idea of related rates where time is a factor. The lecture then delves into Boyle's Law, illustrating how to find the rate of change of pressure with respect to time, emphasizing the importance of understanding constants and their derivatives. The session also covers the application of derivatives in finding the equations of tangent lines to a curve at a given point, highlighting the need for implicit differentiation and the product rule. The lecturer stresses the importance of understanding the context of the problem and the correct application of differentiation rules. The transcript concludes with a discussion on the notation and interpretation of functions, emphasizing the need to correctly identify the independent and dependent variables in various mathematical contexts.
Takeaways
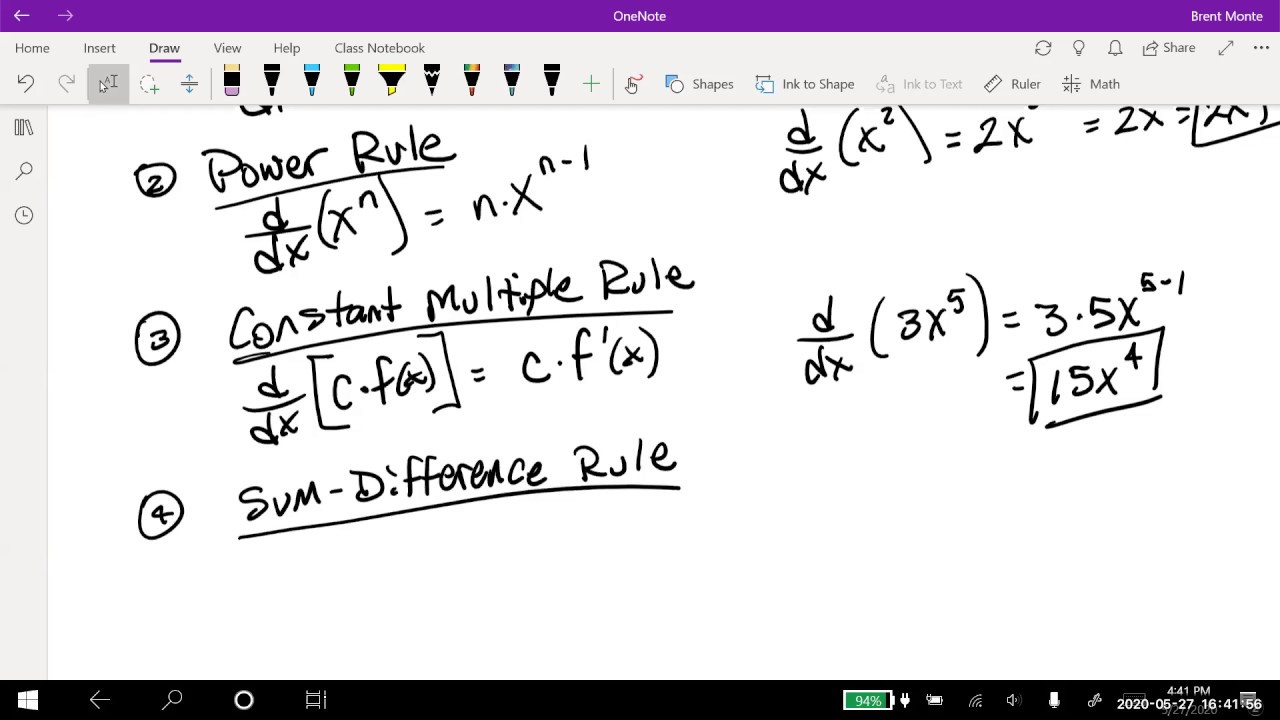
- 📐 The concept of a derivative, denoted as y' or f', represents the rate of change of a function with respect to a variable, typically x.
- 🔄 A differential, dy, represents the actual change in the function, which can be found by multiplying the derivative by the change in x, dx.
- ⏱️ Related rates involve the rate of change with respect to time, where derivatives are taken with respect to dt instead of dx.
- 🔀 When differentiating expressions involving multiple variables, it's crucial to apply the correct rules, such as the product rule, to find the derivative.
- 🧮 Constants, like k in Boyle's Law p/T = k, have a derivative of zero, simplifying the differentiation process.
- 📉 The rate of change of a quantity can be found by differentiating the given relationship with respect to time, as shown with Boyle's Law.
- 📈 To find the equation of a tangent line, one must first determine the slope, which is the derivative of the function at a given point.
- 🔢 When solving for derivatives in implicit form, every term in the equation must be differentiated, which can lead to complex expressions requiring careful application of derivative rules.
- 🎓 Students should be aware of the notation and understand that x(t) implies a function of t, and the derivative x' will be with respect to t.
- 📌 Points on a graph or curve are typically represented as (x, y), but when dealing with functions like x(t), the point is represented as (t, x).
- 📝 When solving problems involving rates of change, it's important to include units in the final answer to convey the meaning of the numerical result accurately.
Q & A
What is the concept of the derivative in the context of the course?
-The derivative is the change in rate of a function with respect to its variable, often denoted as 'y prime' or 'f prime'. It represents how the function's rate of change varies as the input changes.
What is a differential and how does it relate to the derivative?
-A differential, denoted as 'dy', represents the actual change or 'jump' in the function's value. It is related to the derivative as it is the product of the derivative (dy/dx or dy/dt) and the change in the independent variable (dx or dt).
What is the significance of 'related rates' in calculus?
-Related rates involve finding the rate at which one quantity changes with respect to another, often involving time. It is used when there is a relationship between multiple variables, and one seeks to determine how changes in one variable affect another.
How does Boyle's Law relate to the concept of rate of change?
-Boyle's Law states that the pressure of a gas is inversely proportional to its temperature when volume is held constant, expressed as p/T = k. The rate of change of pressure with respect to time can be found by differentiating this relationship with respect to time, yielding dp/dt in terms of the given constants and rates of change.
What is the process for finding the equation of a tangent line to a curve at a given point?
-The process involves first finding the derivative of the function, which gives the slope of the tangent line at any point on the curve. Then, one uses the point-slope form of a line to write the equation of the tangent line, which is y - y1 = m(x - x1), where m is the slope and (x1, y1) is the given point.
How does the concept of implicit differentiation come into play when finding the derivative of an equation?
-Implicit differentiation is used when the equation is not explicitly solved for y, and both x and y are functions of a third variable, often time. It involves differentiating every term in the equation with respect to that variable, applying appropriate rules such as the product rule or chain rule as necessary.
What is the role of the quotient rule in differentiating equations?
-The quotient rule is used when differentiating equations that are in the form of one function divided by another. It states that the derivative of u/v is (v*u' - u*v') / (v^2), where u and v are functions of the variable and u' and v' are their respective derivatives.
How does one determine the correct order of variables when differentiating with respect to time?
-The order of variables is determined by the context of the problem. If the problem states 'x is a function of t' (x(t)), then t is the independent variable and x is the dependent variable. Conversely, if it states 't is a function of x' (t(x)), then x is the independent variable and t is the dependent variable.
What is the importance of understanding the context when solving related rates problems?
-Understanding the context is crucial because it determines which variables are dependent and independent, and thus which derivatives are relevant to the problem. Misinterpreting the context can lead to applying incorrect differentiation rules and arriving at a wrong solution.
What is the correct approach to finding the derivative of an equation involving e^t?
-When differentiating an equation involving e^t, one must apply the standard derivative of the exponential function, which is the function itself, multiplied by the derivative of the exponent. For example, the derivative of e^t with respect to t is e^t.
How does the process of finding the equation of a tangent line differ when the equation is given in a non-standard form, such as x(t) instead of y(x)?
-When the equation is given in a non-standard form, one must first understand the relationship between the variables and then apply the appropriate differentiation rules. The derivative that 'pops out' will be with respect to the variable that is being solved for, which may not be the standard x or y.
Outlines
😀 Understanding Derivatives and Differentials
This paragraph introduces the concept of derivatives as the rate of change of a function y with respect to x, denoted as y' or f'. It also discusses differentials, which are the actual change in y, represented as dy = f' dx. The paragraph emphasizes the importance of understanding the concept of related rates, especially when time is involved, and how to apply derivatives in such scenarios.
🔍 Boyle's Law and Rate of Change
The second paragraph delves into Boyle's Law, which relates pressure (P) and temperature (T) with a constant (k). It explains the process of finding the rate of change of pressure with respect to time by differentiating the given relation, avoiding the quotient rule by multiplying both sides by T, and then applying the product rule to find dp/dt. The paragraph concludes with an example calculation using given values for P and T.
📚 Derivatives in Different Contexts
This part of the script discusses the concept of derivatives in various contexts, emphasizing that the derivative of a constant is zero. It also explores the idea of direct derivatives, which are straightforward to compute. The paragraph highlights the importance of understanding the process and avoiding mistakes, as well as the potential for different letter names in equations.
📈 Calculating the Rate of Change of Pressure
The fourth paragraph focuses on calculating the rate of change of pressure with respect to time. It outlines the steps to find the derivative of pressure, substitutes given values for temperature and pressure, and emphasizes the need to write the final answer with units and the correct interpretation (increasing or decreasing). The paragraph also reminds students to be thorough in their answers to avoid losing marks.
🔢 Implicit Differentiation and Tangent Lines
This section deals with implicit differentiation and finding the equation of a tangent line to a curve at a given point. It explains that the slope of the tangent line is equal to the derivative of the function and guides through the process of differentiating an equation involving x and y. The paragraph also addresses how to handle the given value of x and find the corresponding y value to determine the slope.
🧮 Solving for Derivatives and Tangent Lines
The sixth paragraph continues the discussion on derivatives and tangent lines, providing a step-by-step guide to solving for y' given an equation with x and y. It emphasizes the need to replace x with the given value and solve for y, then use the resulting y values to find the slope and the equations of the tangent lines. The paragraph also highlights the importance of understanding the process to avoid mistakes.
📐 Further Exploration of Derivatives
The seventh paragraph continues to explore the concept of derivatives, particularly in the context of equations and functions. It discusses the need to find x', the derivative of x with respect to t, and provides a detailed explanation of how to approach the problem. The paragraph also touches on the importance of understanding the context and the order of operations when differentiating.
🤔 Challenging Questions and Conceptual Understanding
The eighth paragraph presents a more challenging question involving derivatives and functions of t and x. It emphasizes the importance of understanding the underlying concepts and the order in which to perform operations. The paragraph discusses the potential for confusion when the order of variables is reversed and encourages students to grasp the concept thoroughly to avoid mistakes.
📝 Implicit Differentiation and Function Notation
The ninth paragraph delves deeper into implicit differentiation, emphasizing the importance of understanding function notation and when to apply the product rule. It discusses the concept of x as a function of t and how this affects the derivative, highlighting the need to identify the correct variable to differentiate with respect to.
🏁 Final Thoughts on Differentiation
The final paragraph summarizes the key points discussed in the script, focusing on the importance of understanding the process of differentiation, especially in the context of functions and given points. It provides clarity on how to interpret function notation and when to apply certain differentiation rules. The paragraph concludes with a reminder for students to review and understand the material thoroughly.
Mindmap
Keywords
💡Derivative
💡Differential
💡Related Rates
💡Boyle's Law
💡Implicit Differentiation
💡Quotient Rule
💡Product Rule
💡Chain Rule
💡Tangent Line
💡Rate of Change
💡Constant
Highlights
Started with the concept y = f(x) and introduced the derivative as the rate of change of y with respect to x, denoted as y' or f'(x).
Discussed the concept of differentials, where dy represents the actual change in y and is given by f'(x) dx.
Introduced related rates problems involving time, denoting rates of change with respect to time using dt.
Explained how to apply derivatives in related rates problems by differentiating with respect to time, using examples like dp/dt for pressure.
Worked through an example applying Boyle's Law to find the rate of change of pressure with respect to temperature, using given values.
Stressed the importance of including units and the correct wording in the final answer to avoid losing marks.
Discussed finding the equation of the tangent line to a curve at a given point, emphasizing the need to find the slope (derivative) first.
Demonstrated implicit differentiation when the equation is not explicitly in the form y = f(x), using the product rule.
Solved a problem to find the slope of the tangent line at a point where only the x-value was given, by first solving for y.
Highlighted the need to be careful with the order of variables and applying the correct differentiation rules when the standard x and y are not used.
Explained the concept of a function of a function, and how to determine which variable to differentiate with respect to based on the given equation.
Discussed the importance of understanding the context of the problem to know whether to find dx/dt or dt/dx.
Provided tips for solving related rates problems by identifying the correct variables and applying the appropriate differentiation rules.
Worked through a series of practice problems to illustrate the concepts and techniques discussed, providing step-by-step solutions.
Emphasized the need to practice and review tricky problems to build proficiency in applying derivatives to related rates and tangent line problems.
Encouraged students to make a summary of the key concepts, methods, and problem-solving strategies covered in the lesson.
Reminded students to be careful with the notation and wording in their answers to ensure clarity and avoid losing marks.
Concluded the lesson by encouraging students to continue practicing and reviewing the material to prepare for the exam.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: