Proving Trigonometric Identities | Fundamental Trigonometric Identities | Formulas | Part 2

Prof D
22 Jun 202113:40
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video continues the series on proving trigonometric identities, focusing on simplifying complex expressions into more recognizable forms. The instructor demonstrates step-by-step solutions for four examples, using reciprocal and quotient identities, as well as Pythagorean identities to simplify expressions involving secant, cosine, sine, tangent, and cotangent functions. The goal is to show that the left side of the equations simplifies to match the right side, thus proving the given expressions as identities. The video concludes with an invitation for viewers to ask questions or seek clarifications in the comments section.

Takeaways
  • 📚 The video is a continuation of a series on proving trigonometric identities.
  • 🔍 The presenter uses complex numbers to simplify trigonometric expressions.
  • 📈 Example 5 demonstrates proving the identity secant theta - cosine theta = sine theta * tangent theta.
  • 📉 The reciprocal identity 1/cosine theta is used to simplify expressions involving secant.
  • 🧩 In Example 6, the presenter simplifies cosecant theta over tangent theta + cotangent theta to cosine theta.
  • 🔄 Reciprocal and quotient identities are applied to transform the trigonometric functions into sine and cosine.
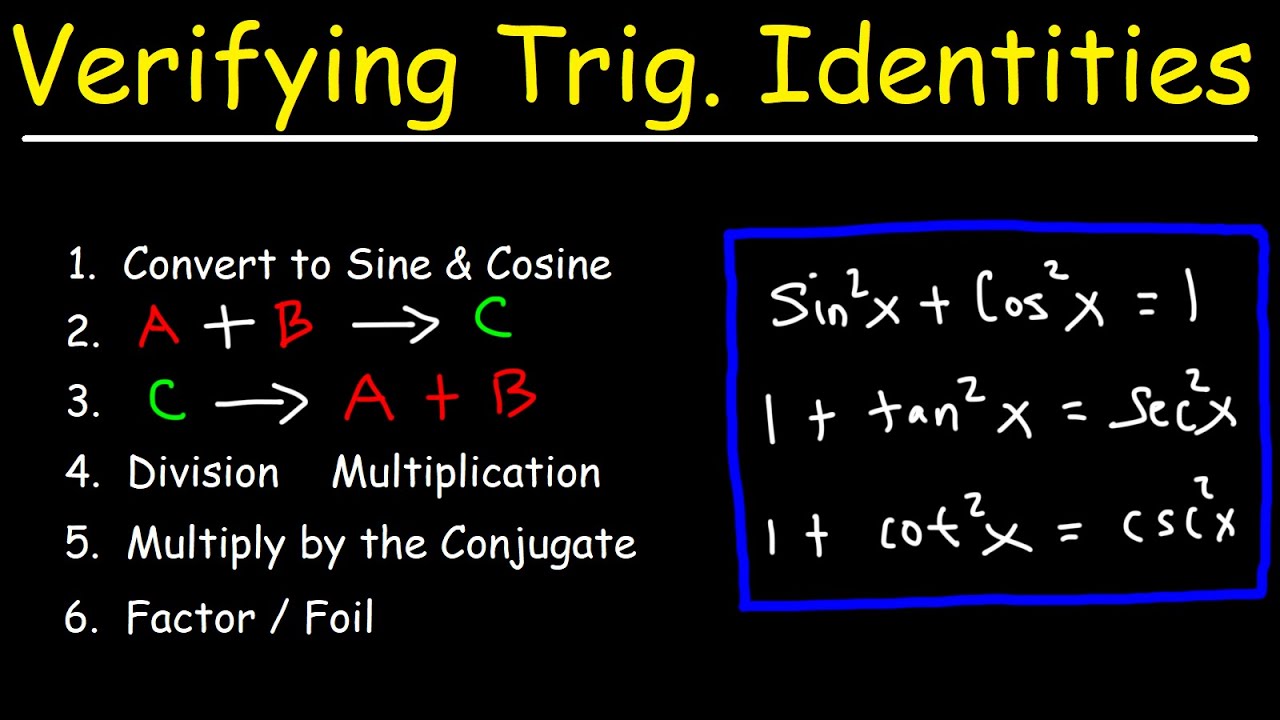
  • 📐 Pythagorean identities are used to further simplify the expressions, such as 1 - cos^2(theta) becoming sin^2(theta).
  • 📘 Example 3 shows the proof of the identity tangent squared x - secant squared x / cosine x = -secant x.
  • 📌 The video explains that secant squared x can be expressed as tangent squared x + 1 using Pythagorean identities.
  • 📊 In Example 8, the identity tangent x * cosecant x * secant x = tangent squared x + 1 is proven.
  • 👨‍🏫 Prof D concludes the video by encouraging viewers to practice proving trigonometric identities and to ask questions in the comments.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is proving trigonometric identities.

  • What is the first example discussed in the video?

    -The first example discusses proving that secant theta minus cosine theta is equal to sine theta times tangent theta.

  • What trigonometric identity is used to simplify secant theta?

    -Secant theta is simplified using the reciprocal identity, which is 1 over cosine theta.

  • How is the left side of the first example simplified?

    -The left side is simplified by combining terms over a common denominator, which is cosine theta, and then applying the Pythagorean identity to express 1 - cosine squared theta as sine squared theta.

  • What is the result of simplifying the left side of the first example?

    -The result of simplifying the left side is sine theta times tangent theta, which matches the right side of the equation, thus proving the identity.

  • What is the second example's goal in proving an identity?

    -The second example aims to prove that cosecant theta over tangent theta plus cotangent theta is equal to cosine theta.

  • How is cosecant theta expressed in terms of sine?

    -Cosecant theta is expressed as the reciprocal of sine theta, which is 1 over sine theta.

  • What is the final simplified form of the left side of the second example?

    -The final simplified form is cosine theta, which matches the right side of the equation, confirming the identity.

  • What is the third example's equation to be proven as an identity?

    -The third example's equation to be proven is tangent squared x minus secant squared x over cosine x equals negative secant x.

  • How is secant squared x simplified using Pythagorean identities?

    -Secant squared x is simplified to tangent squared x plus one, using the Pythagorean identity.

  • What is the final result of simplifying the third example's equation?

    -The final result is negative secant x, which matches the right side of the equation, thus proving the identity.

  • What is the fourth example's equation to be proven as an identity?

    -The fourth example's equation to be proven is tangent x times cosecant x times secant x equals tangent squared x plus one.

  • How are the trigonometric functions in the fourth example simplified?

    -Tangent x is simplified to sine x over cosine x, cosecant x to 1 over sine x, and secant x to 1 over cosine x. The simplification leads to an expression involving sine and cosine squared terms.

  • What is the final form of the fourth example's equation after simplification?

    -The final form is tangent squared x plus one, which matches the right side of the equation, confirming the identity.

  • What advice does the professor give at the end of the video?

    -The professor advises viewers to leave any questions or clarifications in the comments section and thanks them for watching.

Outlines
00:00
📚 Proving Trigonometric Identities: Secant Theta and Cosine Theta

In this educational video, the instructor begins by welcoming viewers back to the channel and continues from a previous lesson on proving trigonometric identities. The focus is on example number five, which aims to prove that secant theta minus cosine theta equals sine theta times tangent theta. The explanation involves simplifying trigonometric functions in terms of sine and cosine, using reciprocal identities to express secant theta as 1 over cosine theta. The instructor then combines terms and applies the LCD method, leading to the Pythagorean identity to show that the left side simplifies to sine theta over cosine theta, which is equivalent to tangent theta. The video demonstrates that the given expression is indeed an identity.

05:03
🔍 Simplifying Trigonometric Expressions: Cosecant Theta and Cotangent Theta

The second paragraph of the video script delves into example number six, which seeks to prove that cosecant theta over tangent theta plus cotangent theta equals cosine theta. The instructor simplifies the expression by converting cosecant theta to 1 over sine theta and tangent theta to sine theta over cosine theta. Cotangent theta is then expressed as cosine theta over sine theta. By combining these with a common denominator of sine theta times cosine theta, the numerator simplifies to sine squared theta plus cosine squared theta. Utilizing the Pythagorean identity, this further simplifies to 1, which when multiplied by the denominator, results in cosine theta. This confirms that the given expression is a valid trigonometric identity.

10:07
📘 Advanced Trigonometric Identity: Tangent Squared X and Secant Squared X

In the third example, the video script presents a more complex identity involving tangent squared x minus secant squared x over cosine x, which is proven to be equal to negative secant x. The instructor simplifies secant squared x using the Pythagorean identity, expressing it as tangent squared x plus one. After distributing the negative sign and simplifying the expression, the result is negative one over cosine x, which is recognized as the reciprocal identity of secant x. This confirms that the left side of the equation simplifies to the right side, validating the identity.

📘 Trigonometric Identity Involving Tangent, Cosecant, and Secant

The final example in the script, example number eight, aims to prove that tangent x times cosecant x times secant x equals tangent squared x plus one. The instructor simplifies the expression by converting tangent x to sine x over cosine x, cosecant x to 1 over sine x, and secant x to 1 over cosine x. Multiplying these together and simplifying, the expression becomes secant squared x, which is known to be equivalent to tangent squared x plus one. This confirms that the equation is an identity, concluding the video with a demonstration of the application of reciprocal and Pythagorean identities in proving trigonometric identities.

Mindmap
Keywords
💡Trigonometric Identities
Trigonometric identities are equations that hold true for all values of the variables involved, typically involving sine, cosine, and tangent functions. In the context of the video, these identities are the main focus, as the speaker is proving various trigonometric identities to demonstrate mathematical relationships. For example, the script mentions proving that 'secant theta minus cosine theta is equal to sine theta times tangent theta,' which is one of the identities discussed.
💡Secant
Secant is the reciprocal of the cosine function, denoted as sec(θ) = 1/cos(θ). It is one of the basic trigonometric functions and is used in various identities. In the video, secant is used in the identity 'secant theta minus cosine theta is equal to sine theta times tangent theta,' where the secant function is simplified to its reciprocal form to prove the identity.
💡Cosine
Cosine is a fundamental trigonometric function that relates the angle of a right triangle to the ratio of the adjacent side over the hypotenuse. It is extensively used in the video to form and prove identities. For instance, 'secant theta minus cosine theta' is an expression that involves the cosine function, and it is simplified using the reciprocal identity of secant.
💡Sine
Sine is another basic trigonometric function that represents the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right-angled triangle. In the video, sine is used in multiple identities, such as 'sine theta times tangent theta,' showing its importance in trigonometric relationships.
💡Tangent
Tangent is the ratio of the sine of an angle to the cosine of the same angle, represented as tan(θ) = sin(θ)/cos(θ). It is used in the video to express and prove identities, such as 'secant theta minus cosine theta is equal to sine theta times tangent theta,' where tangent is a key component of the identity being proven.
💡Cosecant
Cosecant, the reciprocal of the sine function, is denoted as csc(θ) = 1/sin(θ). It is used in the video to simplify expressions and prove identities. For example, in the identity 'cosecant theta over tangent theta plus cotangent theta is equals to cosine theta,' cosecant is used to express the relationship between the functions.
💡Cotangent
Cotangent is the reciprocal of the tangent function, represented as cot(θ) = 1/tan(θ) = cos(θ)/sin(θ). It is used in the video to simplify and prove identities. In the script, cotangent is part of the identity 'cosecant theta over tangent theta plus cotangent theta is equals to cosine theta,' where it is simplified using quotient identities.
💡Pythagorean Identities
Pythagorean identities are fundamental relationships between the sine and cosine functions that are derived from the Pythagorean theorem. They include identities such as sin²(θ) + cos²(θ) = 1. In the video, these identities are used to simplify expressions and prove other trigonometric identities, such as simplifying '1 - cos²(θ)' to 'sin²(θ)'.
💡Reciprocal Identities
Reciprocal identities are relationships that define the reciprocal of trigonometric functions, such as secant being the reciprocal of cosine and cosecant being the reciprocal of sine. In the video, these identities are used to transform expressions into simpler forms, as seen when 'secant theta' is simplified to '1/cosine theta'.
💡Quotient Identities
Quotient identities are expressions that define one trigonometric function as the quotient of two others, such as tangent being sine divided by cosine. In the video, these identities are used to rewrite expressions in terms of sine and cosine, as seen when 'tangent theta' is expressed as 'sine theta over cosine theta'.
💡Simplification
Simplification in the context of the video refers to the process of rewriting trigonometric expressions into simpler forms using identities. This is a key step in proving identities, as it allows for the comparison of both sides of an equation to verify if they are equivalent. The script demonstrates simplification by transforming complex expressions into simpler ones, such as converting 'secant theta minus cosine theta' into 'sine theta times tangent theta'.
Highlights

Introduction to the video on proving trigonometric identities.

Continuation from a previous video on the same topic.

Starting with example number five to prove a trigonometric identity.

The identity to prove: secant theta minus cosine theta equals sine theta times tangent theta.

Assumption that theta can be a complex number.

Simplifying the left side of the identity using reciprocal identities.

Combining terms by finding a common denominator of cosine theta.

Using Pythagorean identities to simplify the expression.

The left side simplifies to match the right side, proving the identity.

Moving on to example number six to prove another identity.

The identity to prove: cosecant theta over tangent theta plus cotangent theta equals cosine theta.

Simplifying the left side using reciprocal and quotient identities.

Finding a common denominator to combine terms.

Simplifying the numerator to show the identity.

The final simplification shows the left side equals the right side, confirming the identity.

Example number three introduces a more complex identity to prove.

The identity to prove: tangent squared x minus secant squared x over cosine x equals negative secant x.

Simplifying the left side using Pythagorean identities and reciprocal identities.

The simplification results in the left side matching the right side, proving the identity.

Example number eight presents another identity to prove.

The identity to prove: tangent x times cosecant x times secant x equals tangent squared x plus one.

Simplifying the left side using quotient and reciprocal identities.

Applying Pythagorean identities to further simplify the expression.

The final expression matches the right side, confirming the identity.

Conclusion of the video with an invitation for questions and clarifications.

Transcripts

Browse More Related Video

Proving Trigonometric Identities | Fundamental Trigonometric Identities | Formulas | Sample Problems

Trig - 0.4 Fundamental Trig Identities

Verifying Trigonometric Identities

Identities Grade 11: Introduction and practice

Ultimate trig identity problem study guide!

5.1.2 Pythagorean Identities

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryMath TutorialIdentity ProofsEducationalStep-by-StepSimplificationMath EducationLearningMath SkillsTutorial