Verifying Trigonometric Identities
TLDRThe video script provides a comprehensive guide on verifying trigonometric identities, a topic that can be challenging but is broken down into manageable steps. The presenter suggests starting by converting everything to sine and cosine, then using various techniques such as finding a common denominator, factoring, and converting between multiplication and division. Key trigonometric identities are emphasized, including sine squared plus cosine squared equals one, and 1 plus tangent squared equals secant squared. The script walks through several examples, showing how to manipulate expressions to verify identities, and encourages viewers to pause and attempt problems themselves. The process involves looking at the right side of the equation as a guide, converting terms into fractions with common denominators when necessary, and simplifying using known identities. The script concludes with a reminder that the goal is to show that the left side of the equation is equivalent to the right side, regardless of the approach taken.
Takeaways
- 📐 **Convert to Sine and Cosine**: Start by expressing everything in terms of sine and cosine functions, which can simplify many trigonometric identities.
- 📄 **Common Denominators**: When there are multiple terms on one side of the equation, find a common denominator to combine them into a single fraction.
- 📈 **Factoring**: If there are two terms on one side and one on the other, factoring can help consolidate terms or vice versa.
- 🔄 **Distribute and Split Fractions**: When you have one term on one side and multiple on the other, distribute or split fractions to match the number of terms.
- 🤝 **Multiply by Conjugate**: If you encounter a plus or minus sign with cosine in the denominator, multiply by the conjugate to simplify.
- 📚 **Memorize Identities**: Key trigonometric identities such as sine squared plus cosine squared equals one should be memorized for easy reference.
- 🔢 **Reciprocal Identities**: Know that tangent is sine over cosine, and that secant and cosecant are the reciprocals of cosine and sine, respectively.
- 🧩 **Use the Right Side as a Guide**: When stuck, look at the right side of the equation to guide your manipulations on the left side.
- 🤔 **Introduce Missing Functions**: If a function is missing on one side of the equation, use known identities to introduce it.
- 🔁 **Convert Division to Multiplication**: Use algebraic tricks to convert division into multiplication, which can simplify expressions.
- ✅ **Verify by Simplification**: The goal is to show that the left side of the equation simplifies to the right side, confirming the identity.
Q & A
What is the main objective when verifying a trigonometric identity?
-The main objective is to show that the left side of the given equation is equivalent to the right side.
What is a common initial step when approaching a trigonometric identity problem?
-A common initial step is to try converting everything to sine and cosine functions.
When there are two terms on the left side and one term on the right, what technique can be used?
-If the terms on the left are fractions, you can try to find a common denominator and convert them into a single fraction.
What is the reverse process of converting two terms into one term in trigonometric identities?
-The reverse process involves distributing from one term to two terms or splitting one fraction into two smaller fractions.
How can you convert division into multiplication in trigonometric identities?
-You can convert division into multiplication by writing the fraction as 'a over 1, times 1 over b'.
What is the significance of multiplying by the conjugate in certain trigonometric identities?
-Multiplying by the conjugate is useful when there is a plus or minus sign with cosine in the denominator of a fraction, as it helps to simplify the expression.
What are some basic trigonometric identities that should be memorized for solving problems?
-Some basic identities include sine squared plus cosine squared equals one, 1 plus tangent squared equals secant squared, and tangent equals sine over cosine.
How can you verify the identity sin(x) * sec(x) = tan(x)?
-By converting secant to its cosine reciprocal and simplifying, you show that sin(x) * (1/cos(x)) = sin(x)/cos(x), which is equal to tan(x).
What is the strategy for verifying the identity tan^2(x) * cot^2(x) = 1?
-By expressing tangent and cotangent in terms of sine and cosine, squaring them, and then simplifying the resulting expression to 1.
In the identity tan(x) * csc(x) * sin(x) = 1, how can you simplify the left side to match the right side?
-By converting cotangent to cosine/sine, secant to 1/cosine, and canceling out the common sine and cosine terms, leaving you with 1.
When faced with a more complex identity like sin(x) * tan(x) = 1 - cos^2(x)/cos(x), what approach can be taken?
-You can start by expressing sine and tangent in terms of sine and cosine, then use the identity sin^2(x) + cos^2(x) = 1 to replace sin^2(x) with 1 - cos^2(x).
How can you approach an identity with two terms on the left and one on the right, such as sin(x) * tan(x) + cos(x) = sec(x)?
-By converting everything to sine and cosine, finding a common denominator for the two terms on the left, and then combining and simplifying to match the single term on the right.
Outlines
📚 Introduction to Verifying Trigonometric Identities
The video begins with an introduction to the process of verifying trigonometric identities, which is acknowledged to be a challenging topic. The presenter outlines a general approach to solving such problems, emphasizing the need to demonstrate that the left side of a given equation is equivalent to the right side. Several techniques are suggested for this purpose, including converting expressions to sine and cosine, finding common denominators, factoring, distributing, and multiplying by the conjugate. The importance of knowing and applying fundamental trigonometric identities is stressed, and viewers are encouraged to take notes as the presenter writes key formulas on the board.
🔍 Converting to Sine and Cosine for Identity Verification
The presenter demonstrates the process of verifying a trigonometric identity by converting everything to sine and cosine functions. The video illustrates this by solving the identity sin(x) * sec(x) = tan(x). The right side of the equation is kept constant while the left side is manipulated to match it. The secant function is converted to its reciprocal, and the resulting expression is simplified to show that the left and right sides are equivalent, thus verifying the identity.
🔢 Simplifying Trigonometric Expressions with Identities
The video continues with more examples of verifying trigonometric identities. The presenter simplifies expressions using the properties of trigonometric functions and their reciprocals. For instance, the identity tan^2(x) * cot^2(x) = 1 is verified by expressing tangent and cotangent in terms of sine and cosine, and then simplifying the expression to 1. The presenter also shows how to handle more complex identities, such as cot(x) * sec(x) * sin(x) = 1, by converting each term to sine and cosine and then simplifying.
📉 Advanced Techniques for Verifying Identities
The presenter tackles more advanced problems, starting with an identity involving cosine, secant, and cotangent. By canceling out common terms and using the relationship between tangent and cotangent, the identity is proven. The video then moves on to an identity involving sine and tangent, which is transformed into an equivalent form using the Pythagorean identity for sine and cosine. The presenter also addresses an identity with cosine squared and sine squared, showing how to rearrange terms to match the right side of the equation.
🧩 Combining Terms and Simplifying Fractions
The final examples involve combining terms with common denominators and simplifying fractions. The presenter shows how to approach an identity with two terms on the left and one on the right by converting everything to fractions with a common denominator and then combining them into a single fraction. This technique is applied to the identity sin(x) * tan(x) + cos(x) = sec(x). The video concludes with another identity, sec(x) - cos(x) = tan(x) * sin(x), which is simplified by finding a common denominator and then using the Pythagorean identity to replace terms, ultimately verifying the identity.
Mindmap
Keywords
💡Trigonometric Identities
💡Verify
💡Sine and Cosine
💡Common Denominator
💡Conjugate
💡Factoring
💡Distribute
💡Reciprocal Identities
💡Multiply by Conjugate
💡Practice Problems
Highlights
The video discusses techniques for verifying trigonometric identities, which is a challenging topic.
A common first step is converting everything to sine and cosine functions.
When faced with two terms on the left and one on the right, find a common denominator for fractions.
Factoring can help convert two terms into one term or vice versa.
Converting division into multiplication is a useful technique, demonstrated in action.
Multiplying by the conjugate is necessary when there's a plus or minus sign with cosine in the denominator.
Factoring and foiling techniques from algebra can be applied to trigonometric expressions.
Memorizing key trigonometric identities is crucial for solving problems efficiently.
The identity sin^2(x) + cos^2(x) = 1 is very common and should be well-known.
Tangent is the reciprocal of cotangent, and secant and cosecant are reciprocals of cosine and sine, respectively.
The video provides a step-by-step guide to verifying the identity sin(x) * sec(x) = tan(x).
For the identity tan^2(x) * cot^2(x) = 1, converting to sine and cosine and squaring them simplifies the expression to 1.
Cotangent times secant x times sine x equals 1 is verified by converting to sine and cosine and simplifying.
Cosine times secant divided by cotangent equals tangent by canceling out common terms.
Sine x times tangent x equals 1 minus cosine squared over cosine x is verified by introducing cosine into the left side.
The identity cos^2(x) - sin^2(x) = 1 - 2 sin^2(x) is proven by using the Pythagorean identity and rearranging terms.
When two terms on the left equal one term on the right, use common denominators and combine into a single fraction.
Secant minus cosine x equals tangent x times sine x by converting to fractions and using the identity sin^2(x) = 1 - cos^2(x).
Transcripts
Browse More Related Video

Identities Grade 11: Introduction and practice

Pythagorean Identities - Examples & Practice Problems, Trigonometry

5.2.1 Proving Trigonometric Identities
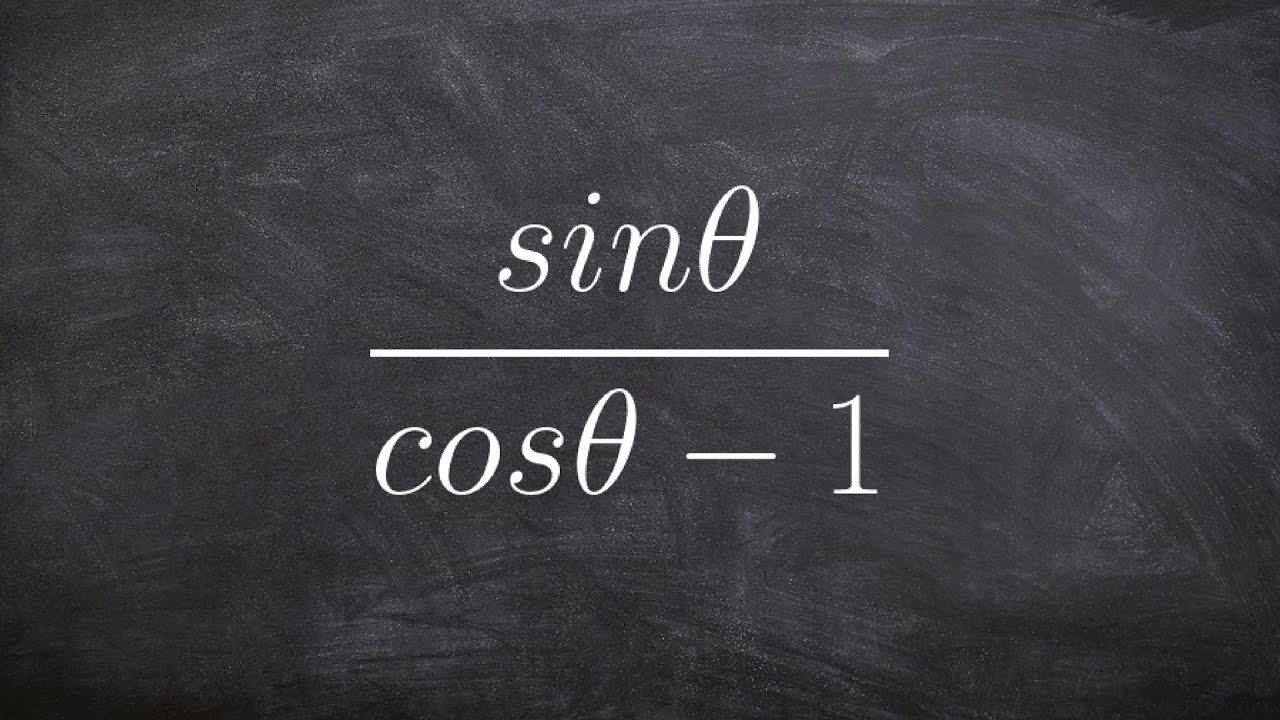
How do you simplify trigonometric expressions
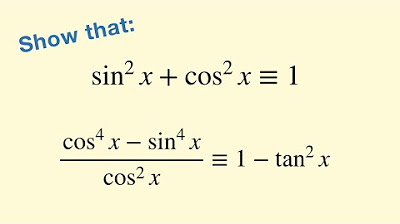
Intro to Trigonometric Identities - part 1

Introduction to Using Trigonometric Identities (Precalculus - Trigonometry 23)
5.0 / 5 (0 votes)
Thanks for rating: