AP Physics 1 - Center of Mass
TLDRThe video script introduces the concept of center of mass, explaining its importance in simplifying the analysis of complex objects. It outlines methods for identifying the center of mass in symmetrical objects with uniform density and systems of multiple objects, using both mathematical formulas and empirical approaches. The distinction between center of mass and center of gravity is also clarified, emphasizing the impact of gravitational fields. The content is practical, informative, and encourages further exploration of the topic.
Takeaways
- 📚 The center of mass is the point at which the mass of an object can be considered to be concentrated for the purpose of simplifying physics calculations.
- 🔍 Identifying the center of mass is crucial for analyzing the motion of an object or system, especially in the context of acceleration, velocity, and position relationships.
- 📏 For objects with uniform density, the center of mass coincides with the geometric center of the object, such as in the case of a symmetric sphere.
- 🤹♂️ Center of mass can be determined empirically by悬挂 an object from different points and finding where the plumb line consistently intersects.
- 🔄 For systems composed of multiple parts, the center of mass is found by calculating the weighted average of the positions of the individual masses.
- 📐 The position vector of the center of mass for a system of point particles is calculated by summing the product of each mass and its position, then dividing by the total mass.
- 🎯 In a two-object system, the center of mass's x and y coordinates can be found by applying the same principle of weighted averages separately for each axis.
- 🔧 The center of gravity is related to the center of mass but specifically refers to the point where gravity acts on an object, assuming uniform gravitational fields.
- 🌐 In non-uniform gravitational fields, the center of gravity and center of mass may not coincide, indicating the complexity of gravitational forces on objects.
- 📝 Mathematical and graphical models are essential tools for analyzing the relationships between acceleration, velocity, and position of the center of mass in a system.
- 🎓 Understanding the concepts of center of mass and center of gravity is fundamental for studying physics and engineering, impacting the analysis and design of various systems.
Q & A
What is the concept of center of mass?
-The center of mass is the point at which the mass of an object, or a system of objects, can be considered to be concentrated. It is the weighted average of the location of mass within the object, making complex objects easier to analyze as if they were a point particle.
How is the center of mass of a uniform density object determined?
-For objects with uniform density, the center of mass is located at the geometric center of the object. For example, the center of mass of a symmetric sphere would be at its exact center.
What method can be used to empirically find the center of mass of an irregular object?
-An empirical method to find the center of mass involves悬挂 the object from different points and drawing a line down the center of the plumb line. Where all these lines cross indicates the center of mass.
How do you calculate the position vector of the center of mass for a system of particles?
-The position vector of the center of mass for a system of particles is calculated by summing the product of each particle's mass and its position, then dividing by the total mass of the system.
What is the relationship between the center of mass and the motion of a system?
-The center of mass can be used to analyze the motion of a system. By understanding the acceleration, velocity, and position of the center of mass, one can gain insights into the overall motion and balance of the system.
How does the center of mass change when combining two objects?
-When combining two objects to find the center of mass, each object's mass and position are considered as a point particle system. The combined center of mass is then calculated based on the total mass and the combined positions of the individual point particles.
What is the difference between center of mass and center of gravity?
-The center of mass is the point where an object's mass is concentrated, while the center of gravity is the location where the force of gravity acts upon the object. In a uniform gravitational field, these two points are the same, but they can differ in non-uniform gravitational fields.
How do you calculate the x-coordinate of the center of mass for a system with two masses on the x-axis?
-The x-coordinate of the center of mass is calculated by taking the product of the mass and its x-coordinate for each particle, summing these products, and then dividing by the total mass of the system.
In a system of particles, how is the y-coordinate of the center of mass determined?
-The y-coordinate of the center of mass is found by multiplying each particle's mass by its y-coordinate, summing these products, and then dividing by the total mass of the system.
What happens to the center of mass when you add more particles to a system?
-As more particles are added to a system, the center of mass will adjust based on the combined mass and position of all particles. The new center of mass will represent the average location of the total mass of the system.
How can the principles of center of mass be applied in real-world scenarios?
-The principles of center of mass are widely applied in various fields such as physics, engineering, and sports. It helps in understanding the balance and motion of complex systems, designing structures, and optimizing the performance of mechanical systems.
Outlines
🌟 Introduction to Center of Mass Concepts
This paragraph introduces the concept of the center of mass, emphasizing its importance in simplifying the mathematical analysis of real-world objects. It explains that the center of mass is the weighted average location of mass within an object, allowing complex objects to be treated as point particles for easier calculations. The paragraph outlines the objectives of the discussion, which include identifying the center of mass in symmetrical objects, analyzing motion in systems of objects, and creating mathematical and graphical models to understand the relationships between acceleration, velocity, and position of the center of mass in a system.
📐 Methods for Finding the Center of Mass
This paragraph delves into the methods of determining the center of mass for various types of objects. It begins by explaining that for objects with uniform density, the center of mass coincides with the geometric center, using a sphere as an example. For more complex objects, the process involves identifying the center of mass of each part and then treating these as a system of point particles to find the overall center of mass. The paragraph also describes the empirical method of hanging an object from different points and intersecting the plumb line for the center of mass. It then provides a detailed example of calculating the center of mass for a system of two objects with given masses and positions, illustrating the application of the mathematical formula for finding the x and y coordinates of the center of mass.
Mindmap
Keywords
💡Center of Mass
💡Uniform Density
💡Point Particles
💡Acceleration
💡Velocity
💡Position
💡System of Particles
💡Geometric Center
💡Weighted Average
💡Empirical Method
💡Center of Gravity
Highlights
Introduction to the concept of center of mass and its importance in simplifying the analysis of complex objects.
Explanation that the center of mass is the weighted average of the location of mass in an object.
Method for finding the center of mass of uniform density objects, which is the geometric center.
Procedure for locating the center of mass of objects with multiple parts by treating them as a system of point particles.
Empirical method of finding the center of mass by hanging the object from different points and using the center of plumb line.
Formula for calculating the position vector of the center of mass for a system of particles.
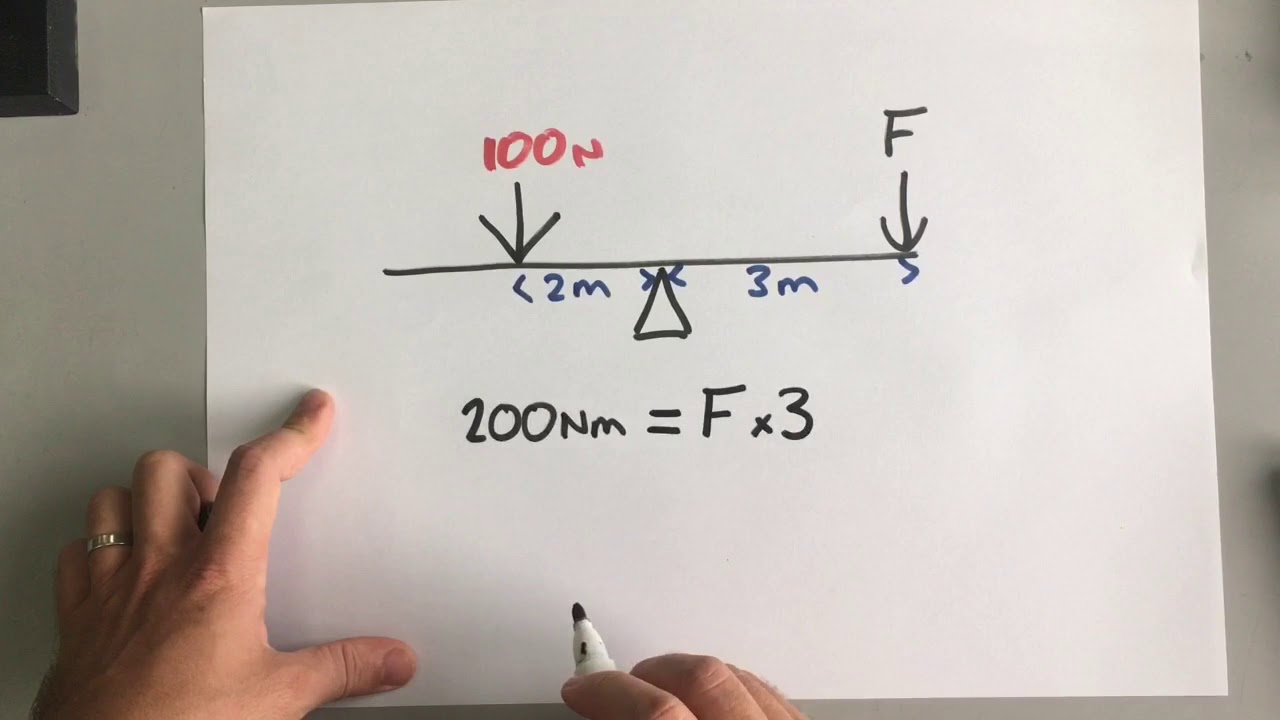
Example problem of finding the center of mass for a simple two-mass system on the x-axis.
Explanation of how to find the center of mass of a more complex object with uniform density.
Calculation of the y-coordinate for the center of mass of a two-object system using point particle methodology.
Problem-solving approach for finding both the x and y coordinates of the center of mass for a system of three point particles.
Brief overview of the difference between center of mass and center of gravity, emphasizing the role of gravitational fields.
Clarification that center of mass and center of gravity are the same in a uniform gravitational field.
Note that in non-uniform gravitational fields, the center of mass and center of gravity may differ.
Encouragement for further exploration of center of mass concepts and resources available on aplusphysics.com.
Closing remarks and well-wishes for a great day, highlighting the informative nature of the discussion.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: