The Feigenbaum Constant (4.669) - Numberphile
TLDRThe video script explores the fascinating world of Feigenbaum's constant, a mathematical constant that emerges from the study of period doubling in bifurcation diagrams, which are used to model population growth and other dynamic systems. The script delves into the logistic map, a simple equation that predicts future population levels based on a fertility parameter, lambda. As lambda increases, the system exhibits different behaviors, from stable populations to extinction and complex oscillations. The period doubling phenomenon, where the system's cycle of behavior doubles with each increase in lambda, leads to the discovery of Feigenbaum's constant, approximately 4.669, which is a universal scaling factor observed across various quadratic maps. The script also touches on the onset of chaos in these systems, where small changes in lambda result in unpredictable and highly sensitive behavior. This concept is not only central to chaos theory and non-linear dynamics but also has practical applications, such as generating pseudo-random numbers for computers. The video concludes with a nod to the interconnectedness of mathematical concepts and the beauty of finding order within chaos.
Takeaways
- 📐 The logistic map is a mathematical function used to predict population growth, which can model how species like rabbits breed over time.
- 🐰 The variable lambda in the logistic map represents fertility; a high lambda means rapid breeding, while a low lambda leads to population decline or extinction.
- 🔁 By iterating the logistic map equation, one can observe how a population's size changes over time, leading to different outcomes such as stabilization, extinction, or oscillation.
- ⚖️ The logistic map demonstrates how small changes in the fertility parameter (lambda) can lead to vastly different population dynamics, illustrating the concept of sensitive dependence on initial conditions.
- 🔢 Feigenbaum's constant (approximately 4.669) is a mathematical constant that describes the rate at which bifurcations (splits in the stable population values) occur in the logistic map as lambda increases.
- 🌐 Feigenbaum discovered that not just the logistic map, but other similar mathematical functions also exhibit period doubling and scale by the same Feigenbaum's constant, indicating a universal behavior across different systems.
- 🛑 Beyond a lambda value of about 3.59, the period doubling observed in the logistic map ceases, and the system enters a chaotic regime where long-term prediction becomes unreliable.
- 🔀 The onset of chaos in the logistic map is characterized by an apparent randomness in population values, despite being generated from a deterministic equation.
- 🔴 The logistic map's chaotic behavior can be exploited to generate pseudo-random numbers, which are useful in computer algorithms that require randomness.
- 🔶 The study of the logistic map and its ensuing chaotic behavior is a foundational element of chaos theory and non-linear dynamics, showing that simple equations can have complex and unpredictable outcomes.
- ✈️ The logistic map and the concept of period doubling are related to the study of fractals, such as the Mandelbrot set, which also exhibits self-similarity and complexity from simple iterative rules.
Q & A
What is Feigenbaum's constant and how is it related to the logistic map?
-Feigenbaum's constant is a mathematical constant that appears in the study of bifurcation diagrams for certain mathematical functions, such as the logistic map. It describes the ratio of successive intervals in which bifurcations occur and is approximately equal to 4.669. It is famous for its universality, appearing in various mathematical contexts that exhibit period doubling.
What is the logistic map and how does it model population growth?
-The logistic map is a mathematical function that models population growth. It takes the form of a quadratic equation, often used to predict the population of a community of animals in the following year based on the current population and a fertility parameter lambda. The function accounts for both breeding and starvation effects by including the previous population size in its calculation.
What is the significance of the lambda parameter in the logistic map?
-The lambda parameter in the logistic map represents the fertility rate of the population. It is a key factor that influences the population growth. A higher lambda value indicates a higher fertility rate, leading to more rapid population growth, while a lower lambda value can lead to a decrease in population or even extinction.
What happens when the lambda value in the logistic map is between 0 and 1?
-When the lambda value is between 0 and 1, the population, over time, tends to die out. This is referred to as the 'Death Zone' in the logistic map, where the population eventually stabilizes at zero.
What is a period doubling, and how does it relate to the logistic map?
-Period doubling is a phenomenon in which a system transitions from having a stable state to oscillating between two values, then four, eight, and so on, doubling the number of states in each transition. In the logistic map, period doubling occurs as the lambda value increases, leading to increasingly complex and unpredictable population dynamics.
What is the significance of the value 3.59 in the logistic map?
-The value 3.59 is significant in the logistic map because it is the point at which period doubling must stop. Beyond this value, the logistic map no longer exhibits period doubling behavior, and the system transitions into what is known as the onset of chaos, where the behavior becomes highly sensitive and unpredictable.
How is the logistic map related to chaos theory?
-The logistic map is one of the simplest examples of a system that exhibits chaotic behavior. As the lambda parameter increases, the system goes through period doubling, eventually leading to chaotic dynamics where the population size is highly sensitive to initial conditions and exhibits unpredictable fluctuations.
What is the connection between the logistic map and the Mandelbrot set?
-The logistic map is connected to the Mandelbrot set through the concept of fractals and chaos. The bifurcation diagram of the logistic map, which shows the stable values of the population over time as lambda increases, is a one-dimensional slice of the Mandelbrot set. Both the logistic map and the Mandelbrot set exhibit self-similarity and complexity at different scales.
How can the logistic map be used to generate pseudo-random numbers?
-The logistic map can be used to generate pseudo-random numbers due to its sensitive dependence on initial conditions. By starting with a small change in the initial population size or lambda value, the system can produce a sequence of numbers that appear random. This property has been used in the past to create one of the early algorithms for generating pseudo-random numbers in computers.
What is the role of Feigenbaum's constant in the study of other mathematical functions?
-Feigenbaum's constant has been found to appear not only in the logistic map but also in other mathematical functions that exhibit period doubling and chaotic behavior. Its universality suggests that it is a fundamental constant in the study of nonlinear dynamics and chaos theory, regardless of the specific function being analyzed.
Why is the logistic map considered a simple yet powerful tool for modeling population dynamics?
-The logistic map is considered simple because it is a quadratic equation with only one parameter that changes. However, it is powerful because it can model a wide range of population behaviors, from stable growth to extinction and chaotic fluctuations, making it a versatile tool for understanding and predicting population dynamics in various contexts.
Outlines
🐇 Introduction to Feigenbaum's Constant and Logistic Map
The video begins with an introduction to Feigenbaum's constant, a mathematical constant related to bifurcation points in the logistic map. The logistic map is a mathematical model used to predict population growth, which is presented as a simple equation involving a variable representing population level and a parameter lambda, representing fertility. The video explains the iterative nature of the logistic map and how it can model population dynamics, such as breeding and starvation, over time. The concept of a fixed point in the iteration is introduced, where the population reaches a stable equilibrium.
📉 Population Dynamics and the Death Zone
The video explores how changing the fertility parameter lambda affects population dynamics. It demonstrates that with low fertility, populations can die out entirely, which is referred to as the 'Death Zone'. The presenter uses the example of setting lambda to 0.65 and shows how the population quickly declines to zero. This section highlights the utility of the logistic map for biologists to model population extinction.
🔁 Periodic Behavior and Bifurcation Points
The video discusses more complex behaviors that emerge from the logistic map when lambda is increased. It shows how the population can enter a two-cycle, where it alternates between two values, and then a four-cycle, indicating a repeating pattern of population sizes over time. This pattern of 'period doubling' is shown to occur at increasing rates as lambda increases, leading to more complex cycles. The presenter also touches on the concept of a 'pitchfork bifurcation', where the stable state of the system splits into multiple cycles.
🎢 Chaos Theory and Feigenbaum's Constant
As lambda increases further, the video explains that the logistic map enters a region of chaotic behavior, where the population sizes become highly unpredictable. The presenter introduces the concept of chaos theory and non-linear dynamics, where simple equations can lead to complex and sensitive outcomes. The video also highlights the discovery of Feigenbaum's constant, a universal ratio that describes how quickly the period doubling occurs across different systems. The constant is shown to be a consistent factor in the period doubling of various quadratic maps, indicating a surprising level of universality in these mathematical systems.
🚀 Final Twist: Beyond Period Doubling and the Birth of Chaos
The video concludes with a discussion of what happens when lambda exceeds 3.59, where period doubling ceases and the system enters a state of fully developed chaos. The presenter creates a visual representation of this transition, showing how the orderly patterns give way to a chaotic and seemingly random distribution of population values. The video also makes a connection to the Mandelbrot set and the broader implications of chaos theory, including its use in generating pseudo-random numbers for computers. Lastly, the presenter provides a resource for further learning through the Great Courses Plus.
Mindmap
Keywords
💡Feigenbaum's constant
💡Logistic map
💡Period doubling
💡Chaos theory
💡Pseudo-random numbers
💡Mandelbrot set
💡Bifurcation diagram
💡Population growth
💡Sensitivity to initial conditions
💡Non-linear dynamics
💡Fractal
Highlights
Feigenbaum's constant is a famous irrational number, similar in significance to pi and e, and is related to the study of bifurcation in mathematical functions.
The logistic map is a mathematical function used to model population growth, which can predict the next year's population for a community of animals.
The logistic map includes a variable lambda, representing fertility, which can be adjusted to model different population behaviors.
Starting with a population level of 1/2 and a fertility lambda of 2.3, the model demonstrates how populations can stabilize over time.
As lambda increases, the model can exhibit more complex behavior, including population cycles and chaotic dynamics.
The period doubling phenomenon, where the population stabilizes in a cycle that doubles with each increase in lambda, is a key aspect of the logistic map's behavior.
Feigenbaum's constant, approximately 4.669, describes the ratio of consecutive gaps between bifurcation points in the logistic map.
The logistic map and Feigenbaum's constant have been found to apply to a wide range of mathematical functions, suggesting a concept of universality.
The onset of chaos in the logistic map occurs when lambda exceeds approximately 3.59, leading to unpredictable and sensitive behavior to initial conditions.
The logistic map's chaotic behavior is an example of a fractal, with self-similar patterns appearing at different scales.
The logistic map's period doubling and chaotic behavior were foundational to the development of chaos theory and non-linear dynamics.
The logistic map function was one of the first used to generate pseudo-random numbers for computers, due to its unpredictable outcomes.
The study of the logistic map and Feigenbaum's constant has practical applications in understanding complex systems and generating random numbers.
The Great Courses Plus offers a vast library of in-depth courses, including topics on mathematics and fractals, similar to the concepts discussed in the logistic map.
The logistic map demonstrates how simple deterministic equations can lead to complex and unpredictable results, which is a central theme in chaos theory.
The video provides a visual representation of the logistic map's behavior, including stable points, cycles, and the transition to chaos, which is crucial for understanding its implications.
Transcripts
Browse More Related Video
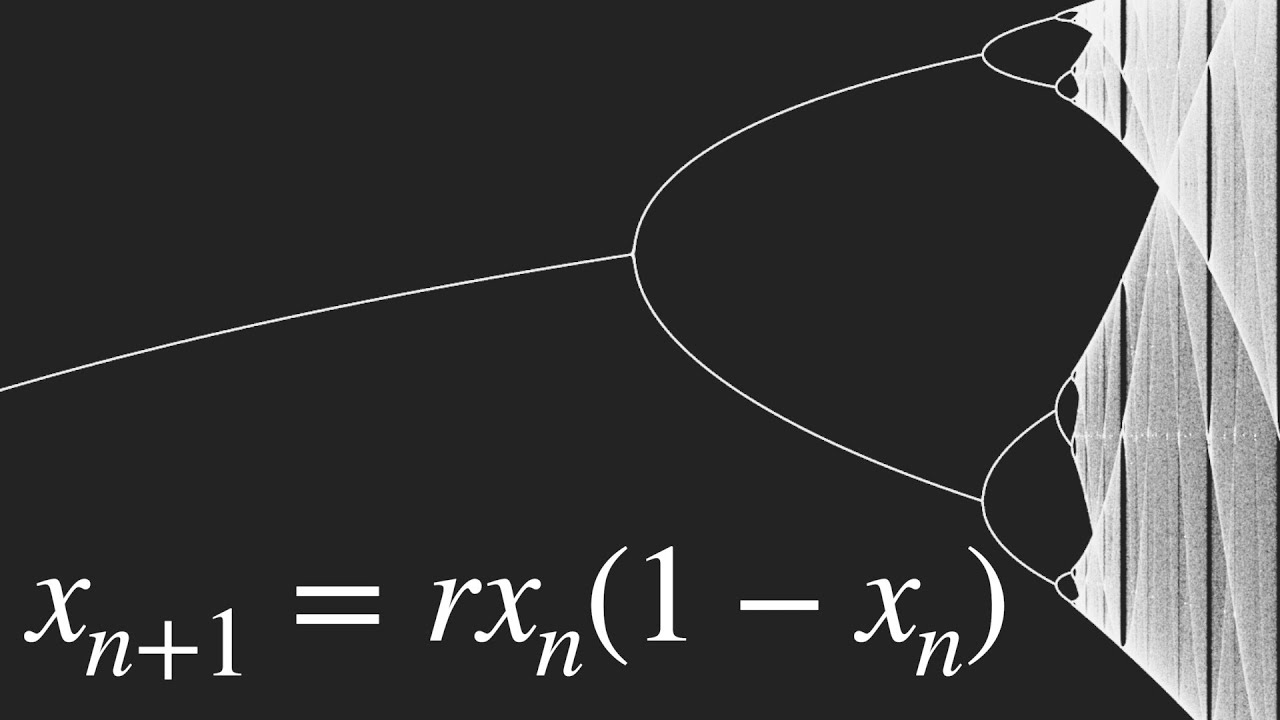
This equation will change how you see the world (the logistic map)

Is the Logistic Map hiding in the Mandelbrot Set? | #SoME3
Chaos Theory: the language of (in)stability

L1.1 General problem. Non-degenerate perturbation theory

The Logistic Equation

Lyapunov's Fractal (that Lyapunov knew nothing about) #SoME2
5.0 / 5 (0 votes)
Thanks for rating: