An Introduction to Integration
TLDRThe video script explains the concepts of differentiation and integration in calculus. It outlines the process of differentiation, which involves multiplying by the power and then subtracting one from the exponent. The opposite process, integration, is described as adding one to the power and dividing by the new exponent, with the inclusion of a constant 'c' to account for any lost constant during differentiation. The script provides examples of both differentiation and integration, demonstrating how to apply these rules to various functions. It also shows how to find the original function from its derivative by integrating and using given coordinates to determine the constant 'c'.
Takeaways
- 📚 Integration is the inverse process of differentiation, used to find the original function given its derivative.
- 🔢 The process of differentiation involves multiplying by the power and then subtracting one from the exponent.
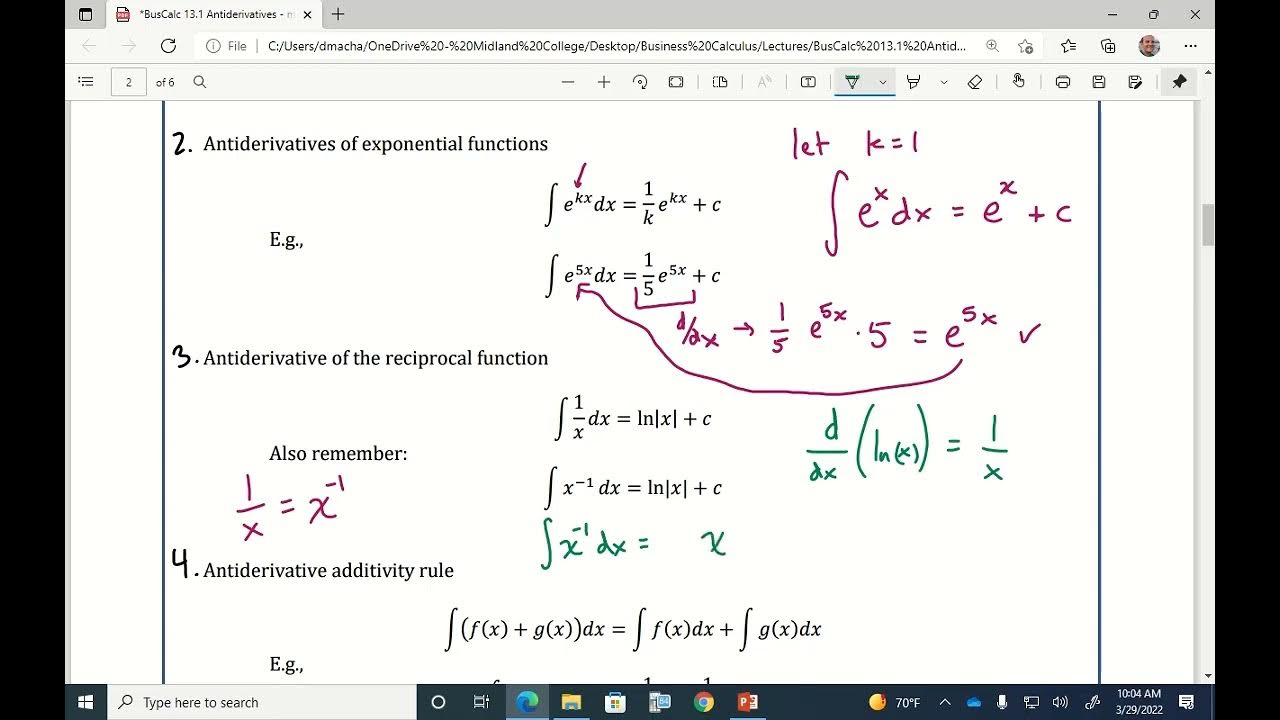
- ⚙️ To integrate, reverse the differentiation process by adding one to the exponent and dividing by the new power.
- 🎯 The integral symbol (∫) denotes the operation of finding the antiderivative or the integral of a function.
- 📈 The constant 'c' is added to the end of an integral to account for the constant of integration, which is lost during differentiation.
- 🌟 When differentiating, any constant term will disappear, and when integrating, it reappears as the constant 'c'.
- 🔄 The process of changing from a derivative to the original function is called integration, and it's a fundamental concept in calculus.
- 📊 The video provides examples of integrating polynomial functions, demonstrating the step-by-step process of adding exponents and dividing.
- 🛠️ The video also covers more complex examples, such as integrating functions with variables in the denominator and roots.
- 📝 To solve for 'y' in terms of 'x', given a derivative and a point, one must integrate the derivative and then apply the point to find the constant 'c'.
- 🔍 The video emphasizes the importance of understanding the relationship between differentiation and integration for solving calculus problems.
Q & A
What is the opposite process of differentiation in calculus?
-The opposite process of differentiation is integration.
How does the process of differentiation involve the power of a term?
-In differentiation, you multiply by the power of the term and then subtract one from the power.
What is the general rule for integrating a term with respect to x?
-The general rule for integrating a term with respect to x is to add 1 to the power of the term and then divide by the new power, followed by adding a constant 'c' at the end.
What happens to a constant term when differentiating?
-When differentiating, a constant term disappears because the power of a constant is 0, and anything to the power of 0 is 1, which does not affect the result.
How do you find the integral of the function 6x^2 + 18x + 5?
-To find the integral of the function 6x^2 + 18x + 5, you would integrate each term, resulting in (6/3)x^(2+1) + (18/2)x^(1+1) + 5x^(0+1) + c, which simplifies to 2x^3 + 9x^2 + 5x + c.
What is the significance of the 'plus c' at the end of an integral expression?
-The 'plus c' at the end of an integral expression represents the constant of integration, which accounts for any constant term that may have been present in the original function before differentiation.
How do you simplify the integral of 3x^3 + 4x^2 + 5x + c?
-The integral simplifies by dividing the coefficients by the new powers: 3x^3 remains as it is, 4 divided by 3 gives 4/3 x^2, and 5 remains as 5x. So, the simplified integral is 3x^3 + (4/3)x^2 + 5x + c.
What is the process for integrating a term with a negative exponent?
-For integrating a term with a negative exponent, you add 1 to the exponent, divide by the new power, and then take the reciprocal of the new power because dividing by a fraction is the same as multiplying by its reciprocal.
How do you find the expression for y in terms of x when given d/dx(y) = 3x^2 + 5x + 10 and the point (2, 3)?
-First, integrate the derivative to get y = x^3 + (5/2)x^2 + 10x + c. Then, substitute the point (2, 3) to find c: 3 = (2^3) + (5/2)(2^2) + 10(2) + c. Solve for c to get c = -35. Thus, the expression for y in terms of x is y = x^3 + (5/2)x^2 + 10x - 35.
What is the integral of 10/x^2 expressed as an integral of a term with a positive exponent?
-The integral of 10/x^2 can be expressed as an integral of a term with a positive exponent by rewriting it as 10x^(-2), which simplifies to -10x^(-1) or -10/x.
How do you handle a term with a square root in integration?
-To handle a term with a square root in integration, you rewrite the square root as a half power, for example, √x becomes x^(1/2), and then you proceed with the integration process by adding 1 to the power and dividing by the new power.
Outlines
📚 Introduction to Integration and Differentiation
This paragraph introduces the concept of integration as the inverse process of differentiation. It explains the process of differentiation by illustrating the steps of multiplying by the power and then subtracting one from the exponent. The paragraph then transitions to integration, describing the process as the opposite of differentiation, which involves adding one to the power and dividing by the new power. The concept of the constant 'c' in integration is also introduced, representing any number that could have been present and disappeared during differentiation.
🔢 Solving Integration Problems with Various Functions
This paragraph delves into solving more complex integration problems. It demonstrates how to integrate functions with different powers and constants, emphasizing the process of adding one to the power, dividing by the new power, and including the constant 'c' at the end. The paragraph also covers the simplification of expressions and the handling of terms that initially seem unintegrated, such as 'root x' or '10 over x squared', by transforming them into integrable forms.
🔍 Applying Integration to Given Differentiation Equations
The focus of this paragraph is on applying integration to specific differentiation equations provided in the question. It shows how to reverse the process of differentiation to find the original function 'y' in terms of 'x', using given values for 'x' and 'y'. The paragraph also explains how to determine the value of the constant 'c' by substituting these known values into the integrated equation, resulting in an expression for 'y' that is a function of 'x'.
📈 Finding the Function 'f(x)' from its Derivative
This paragraph addresses the task of finding the original function 'f(x)' from its derivative 'dy/dx'. It outlines the process of integrating the derivative to recover the function and using a given point to find the value of the integration constant 'c'. The paragraph concludes with the final expression for 'f(x)', which is derived by substituting the values of 'x' and 'y' from the provided coordinates into the integrated equation and solving for 'c'.
Mindmap
Keywords
💡Integration
💡Differentiation
💡dy/dx
💡Power Rule
💡Constant of Integration
💡Indefinite Integral
💡Polynomial Function
💡Integrand
💡Substitution
💡Integration by Simplification
Highlights
The video discusses the process of integration, which is the opposite of differentiation.
Differentiation is explained as multiplying by the power and then subtracting one from the power.
Integration involves adding 1 to the power, dividing by the new power, and including a constant 'c'.
The video demonstrates the integration of a polynomial function, 6x^2 + 18x + 5.
Integration by parts is briefly mentioned, where a function is broken down into simpler parts for easier integration.
The concept of 'u' and 'dv' is introduced as a method for more complex integrations.
The video provides an example of integrating x^5 by adding 1 to the power and dividing by the new power.
The process of integrating a function with a constant term is demonstrated.
Integration of a function with a term to the power of zero is explained, where anything to the power of zero is considered as 1.
The video shows how to integrate a function with a term to the power of -2, by changing the term to x^(-1) and integrating.
The concept of 'plus c' in integration is explained as a way to account for the constant that disappears during differentiation.
An example is given where the integral of 10/x^2 is found by first rewriting the term as 10x^(-2).
The video demonstrates the integration of a radical expression, such as √x, by rewriting it as x^(1/2).
The process of finding the original function 'y' from its derivative 'dy/dx' is explained as integration.
A specific example is worked out where the function y is found in terms of x, given a derivative and a point (x=2, y=3).
The method of finding the constant 'c' in an integral by using a given point is demonstrated.
The video concludes with another example of finding the original function 'f(x)' from its derivative 'f'(x), using integration and a given point.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: