Antidifferentiation
TLDRThis video script discusses anti-derivatives, explaining how they are related to derivatives and how adding a constant to an antiderivative still results in an antiderivative. It covers basic anti-differentiation rules, including the reverse power rule, constant multiple rule, and handling of trigonometric functions. The script also demonstrates solving differential equations and particle motion problems using anti-derivatives.
Takeaways
- 📚 An antiderivative (denoted as \( \int f(x) \, dx \) or \( F(x) \)) is a function whose derivative is equal to the original function \( f(x) \).
- 🔍 Adding a constant \( c \) to an antiderivative does not change its status as an antiderivative of the original function.
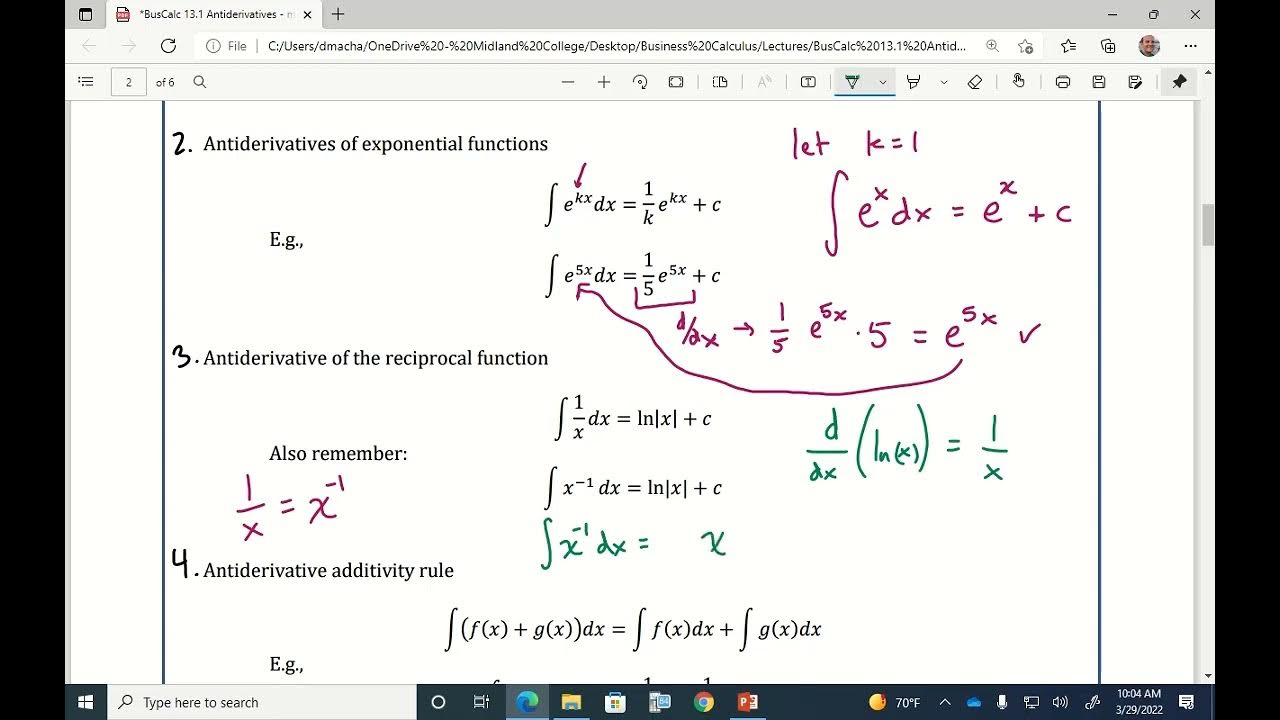
- 🔑 The power rule for antiderivatives states that the antiderivative of \( x^n \) is \( \frac{x^{n+1}}{n+1} \) plus a constant \( c \), where \( n \neq -1 \).
- 📉 For the function \( f(x) = 0 \), any constant \( c \) is an antiderivative, as the derivative of a constant is zero.
- 📈 The antiderivative of a constant \( k \) times a function \( g(x) \) is \( k \) times the antiderivative of \( g(x) \).
- 🌟 The antiderivative of \( \sin(x) \) is \( -\cos(x) \), and for \( \cos(x) \), it's \( \sin(x) \), both plus a constant.
- 🔄 The process of finding antiderivatives can involve reversing the steps of differentiation, such as using the reverse power rule.
- 📝 The notation for antiderivatives involves using 'with respect to' (∫) and 'dx' to denote the variable being integrated.
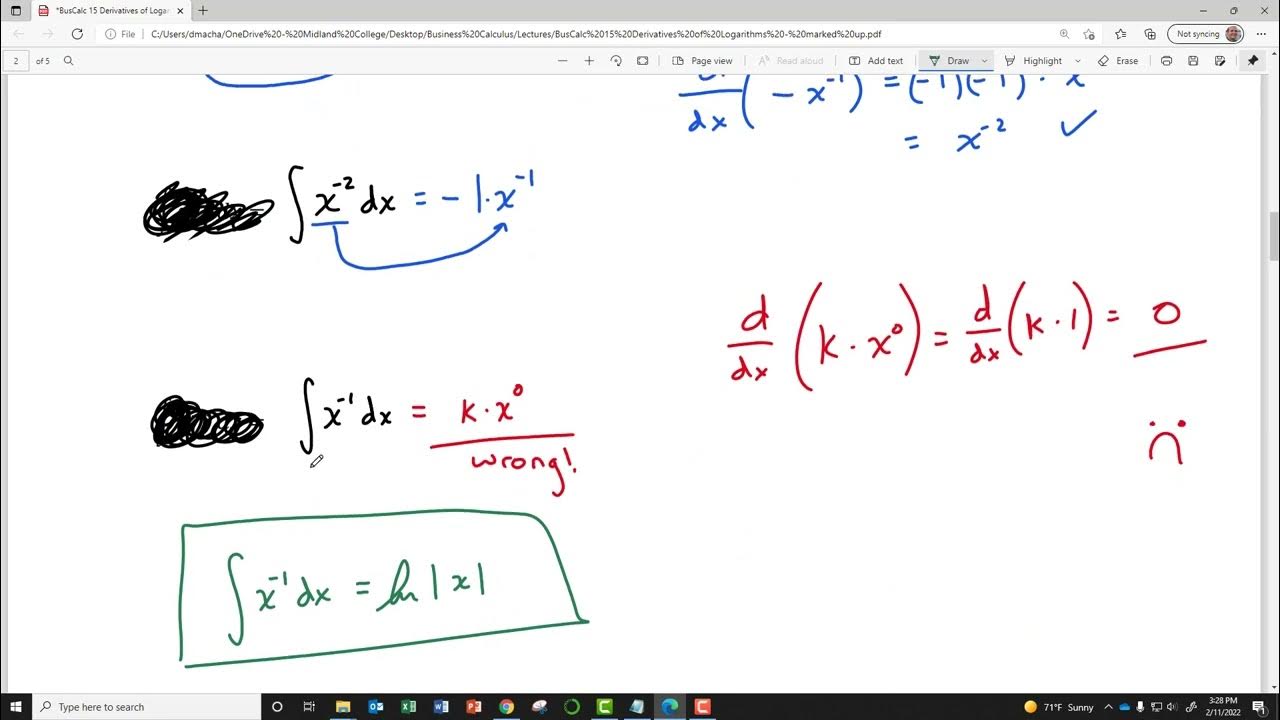
- 🔍 The antiderivative of a function can be found using known integration rules or by looking it up in a table of integrals.
- 🚀 In physics, antiderivatives are used to find quantities like displacement from velocity, which is an application of calculus to motion problems.
- 🔧 Solving differential equations to find original functions involves using given derivatives and initial conditions to determine the function and its constants.
Q & A
What is an antiderivative?
-An antiderivative, also known as an indefinite integral, is a function F(x) such that the derivative of F(x) is equal to the original function f(x). In other words, if F'(x) = f(x), then F(x) is an antiderivative of f(x).
If F(x) is an antiderivative of f(x), what is the effect on the antiderivative if we add a constant c to F(x)?
-Adding a constant c to an antiderivative F(x) does not change its property of being an antiderivative of f(x). The new function F(x) + c will still have a derivative equal to f(x), making it another valid antiderivative.
What is the reverse power rule for antiderivatives?
-The reverse power rule states that the antiderivative of x^n, where n is a real number, is (x^(n+1))/(n+1) + C, where C is the constant of integration.
How do you find the antiderivative of a function that is a constant multiple of another function?
-The antiderivative of a constant multiple k times a function g(x) is simply k times the antiderivative of g(x), or k * integral(g(x) dx).
What is the antiderivative of sine x?
-The antiderivative of sine x is negative cosine x, or -cos(x) + C, where C is the constant of integration.
What is the antiderivative of a function that is the sum of two other functions, f(x) + g(x)?
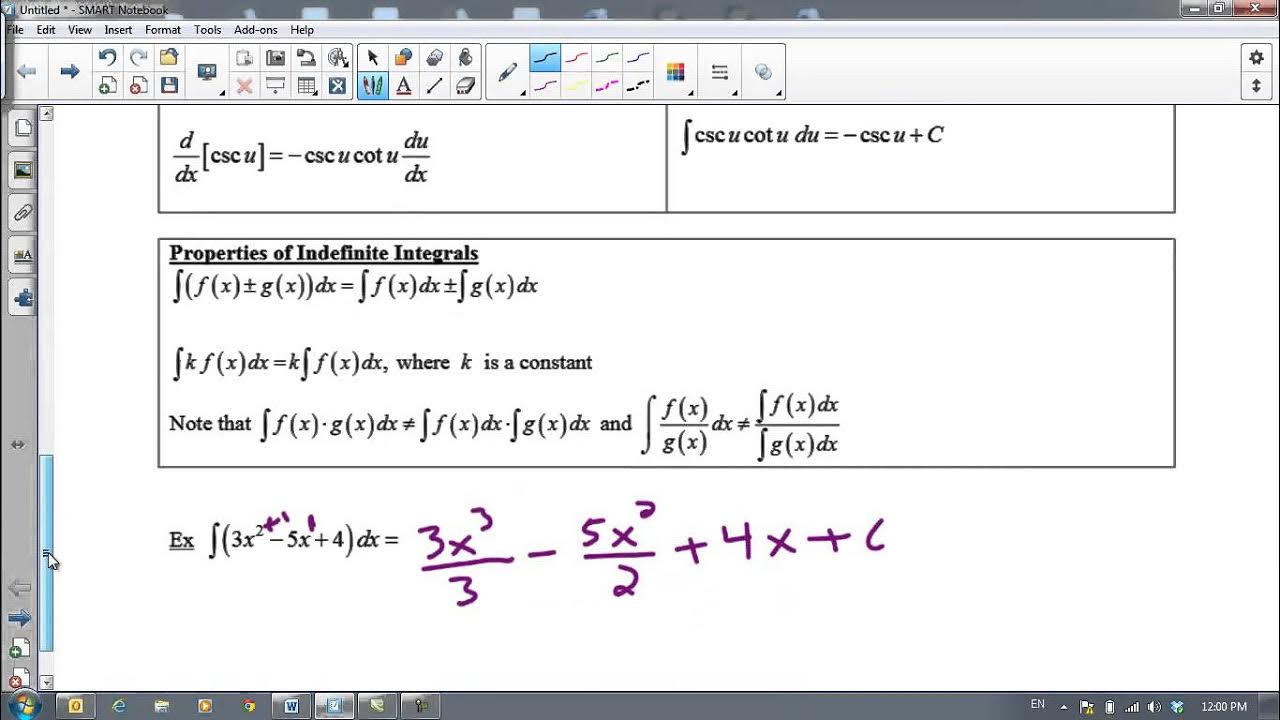
-The antiderivative of the sum of two functions is the sum of their antiderivatives, which can be expressed as integral(f(x) + g(x) dx) = integral(f(x) dx) + integral(g(x) dx).
What is the antiderivative of x squared?
-The antiderivative of x squared, or x^2, is one third of x cubed, or (1/3)x^3 + C, where C is the constant of integration.
How do you find the antiderivative of a function given its derivative?
-To find the antiderivative of a function given its derivative, you apply the appropriate antidifferentiation rules, such as the reverse power rule, and consider the constant of integration for each term.
What is the significance of the constant of integration, C, in antiderivatives?
-The constant of integration, C, accounts for the family of functions that are all antiderivatives of a given derivative. It represents the undetermined constant that arises because the derivative of a constant is zero.
Can you provide an example of solving a differential equation to find a function given its derivative and an initial condition?
-Yes, for example, if we have a differential equation where the derivative of a function f(x) is given by f'(x) = x^2, and we know that f(1) = -4, we can find the function by integrating x^2 to get f(x) = (1/3)x^3 + C and then using the initial condition to solve for C, resulting in f(x) = (1/3)x^3 - 11.
Outlines
📘 Introduction to Antiderivatives
In this section, we discuss the concept of antiderivatives. If f(x) is a function, then F(x) is an antiderivative of f(x) if f(x) is the derivative of F(x). This leads to the fact that if F(x) is an antiderivative, adding any constant c to F(x) still results in an antiderivative. Examples are provided to illustrate how to find original functions from given derivatives.
📚 Basic Antidifferentiation Rules
This section outlines fundamental rules for antidifferentiation. It covers the antiderivative of zero, a constant, and x^n, using the reverse power rule. The constant multiple rule and the linearity of antiderivatives are discussed, emphasizing the importance of adding a constant c to each antiderivative.
🧮 Antiderivatives of Trigonometric Functions
Here, the focus is on finding antiderivatives of trigonometric functions such as sin(x), cos(x), and others. The importance of considering the negative signs and the preparation for future lessons on more complex antiderivative rules is highlighted. Examples of using trigonometric identities to find antiderivatives are also provided.
🔄 Using the Reverse Power Rule and Solving Differential Equations
This section delves into using the reverse power rule for antidifferentiation and solving basic differential equations. Techniques for handling expressions like x raised to fractional powers and converting expressions to exponential form are discussed. Methods for solving elementary differential equations and examples involving constant acceleration are provided.
🚀 Solving Problems with Initial Conditions
In this part, problems involving initial conditions are solved step-by-step. By using given conditions, constants of integration are determined, and specific functions are derived. Examples include solving for particle position given velocity functions and applying these techniques to real-world contexts like motion problems.
⚙️ Solving for Position with Constant Acceleration
The final section addresses finding the position of a particle under constant acceleration. By integrating the acceleration function to find velocity, and then integrating the velocity to find position, complete solutions to motion problems are provided. Examples illustrate how to use initial conditions to solve for constants and find specific positions at given times.
Mindmap
Keywords
💡Anti-derivatives
💡Derivative
💡Constant of Integration (c)
💡Power Rule
💡Linearity
💡Trigonometric Functions
💡Differential Equations
💡Chain Rule
💡Particle Motion
💡Notation
Highlights
Introduction to anti-derivatives and their relationship with derivatives.
Explanation of how adding a constant to an antiderivative still results in an antiderivative.
Proof that the derivative of an antiderivative plus a constant is the original function.
Examples of finding anti-derivatives for basic functions like 4x, x squared, and sine x.
The importance of the plus c in anti-derivatives to account for all possibilities.
Formalization of the reverse power rule for anti-differentiation.
Basic anti-differentiation rules for constants and polynomials.
Constant multiple rule for anti-derivatives and its relation to derivative properties.
Linearity of anti-derivatives for addition and subtraction of functions.
Anti-derivatives of trigonometric functions and the role of plus c.
The process of finding anti-derivatives for composite functions using trigonometric identities.
The use of technology, like a calculator, to find anti-derivatives of complex functions.
The notation for anti-derivatives and its significance in calculus.
Examples of anti-derivatives for various functions including square roots and negative exponents.
Solving differential equations to find functions given their derivatives.
Application of anti-derivatives in physics for problems involving particle motion.
The method of finding position functions for particles in motion using anti-derivatives.
The use of initial conditions to determine the constant c in anti-derivatives.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: