Math 1325 Lecture 9 3
TLDRThe video script offers a comprehensive introduction to the concept of rates of change in algebra, specifically focusing on average and instantaneous rates of change. It explains that the average rate of change, often symbolized by the slope between two points, is calculated as the difference in y-values divided by the difference in x-values. The script then delves into calculus, where the instantaneous rate of change is determined using derivatives. It clarifies that derivatives are akin to the concept of a limit, bringing two points infinitely close to identify the slope at a single point. The video also touches on the application of derivatives in real-world scenarios, such as calculating marginal revenue. It guides viewers through the process of finding derivatives, applying limits, and solving for the equation of a tangent line at a specific point. The summary emphasizes the practicality of derivatives in understanding the rate of change at any given moment, and how it can be applied to various mathematical and economic problems.
Takeaways
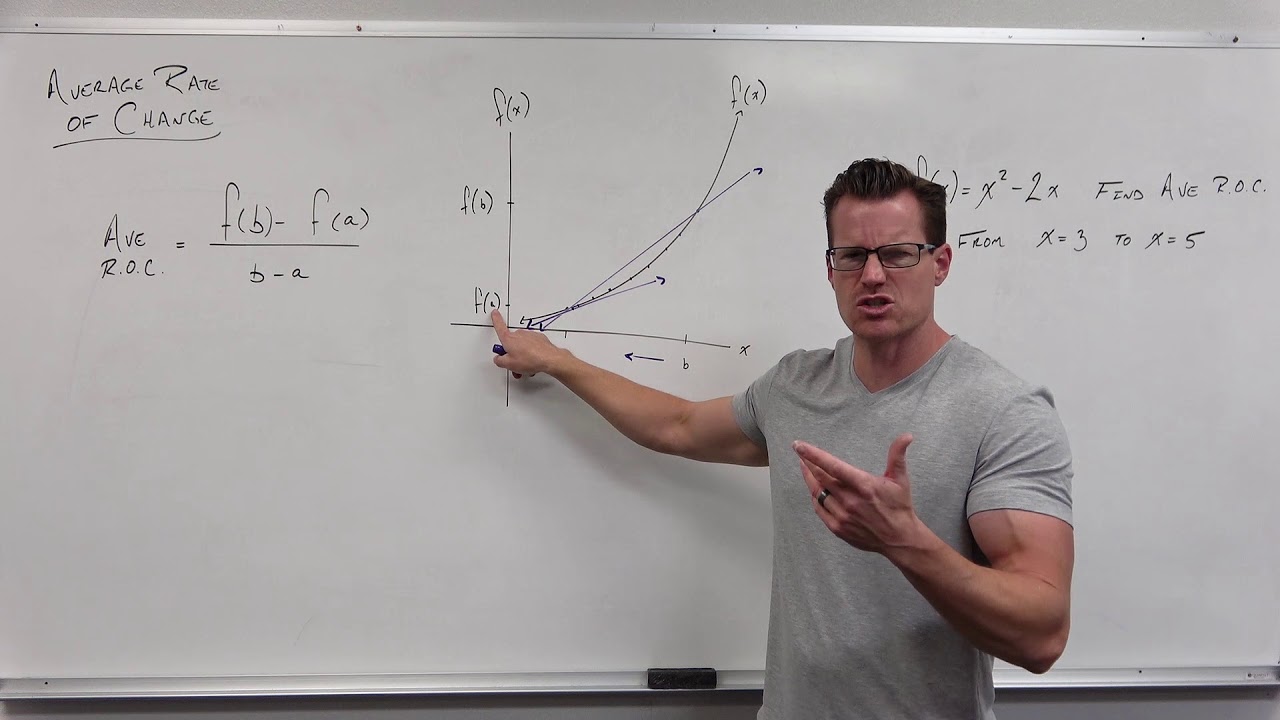
- 📐 The concept of average rate of change in algebra is analogous to the slope between two points, calculated as the rise over run or the difference in y values over the difference in x values.
- 🚀 Velocity is an example of a common rate of change, representing the rate of change of position or distance over time.
- ✍️ When solving word problems, it's crucial to include units in your answers, such as dollars, feet, or time periods.
- 🧮 Calculus extends the idea of average rate of change to instantaneous rate of change, which is found using the concept of a derivative.
- 🔑 The derivative is calculated using the difference quotient, which is then simplified and the limit is applied as the change in x (h) approaches zero.
- 📈 The derivative of a function at a specific point gives the instantaneous rate of change at that point, which is the slope of the tangent line to the function at that point.
- 📉 In economics, marginals represent the additional revenue, cost, or profit associated with one more unit, and for linear functions, the marginal is constant and equals the slope of the function.
- 🔍 For non-linear functions, the marginal revenue or cost at any point is found by taking the derivative of the respective function at that point.
- 📌 To find the equation of the tangent line to a curve at a specific point, you need to determine the slope (derivative) at that point and a point on the line.
- 🧷 The general form of the equation of a line is Y = Mx + B, where M is the slope and B is the y-intercept.
- 🔗 The process of finding the derivative involves substituting (x + h) into the function, simplifying, finding the change in Y values, forming the difference quotient, and applying the limit as h approaches zero.
- 📝 The derivative, denoted as f'(x) or F(x) with an apostrophe, represents the slope of the function at a given point and is a fundamental concept in calculus.
Q & A
What is the definition of average rate of change in the context of algebra?
-The average rate of change in algebra is defined as the slope between two points, which can be calculated as the difference in y-values of the two points divided by the difference in x-values of the same points.
How is velocity related to the concept of rate of change?
-Velocity is a common example of a rate of change, as it represents the rate of change of position or distance with respect to time.
What is the significance of including units in answers to word problems in calculus?
-Including units in answers to word problems is important because it provides context and clarity to the result, whether it's in dollars, feet per unit, or a period of time, etc.
What is the difference between calculus and algebra in terms of rate of change?
-While algebra deals with average rates of change, such as slopes between two points, calculus focuses on instantaneous rate of change, which is the rate of change at a specific point and is found using derivatives.
How is the concept of a derivative related to the difference quotient from algebra?
-The derivative is related to the difference quotient from algebra by adding the concept of a limit. As the difference (H) approaches zero, the derivative gives the slope at a single point, which is the instantaneous rate of change.
What is the process to find the formula for the instantaneous rate of change at any value of x?
-To find the formula for the instantaneous rate of change at any value of x, first find the formula for the second point f(x + h) by substituting (x + h) for every x in the original function f(x). Then calculate the numerator (change in y-values) using f(x + h) - f(x). Form the difference quotient by dividing by h, simplify, and apply the limit as h approaches zero.
How do you find the instantaneous rate of change at a specific point, say x = 2?
-To find the instantaneous rate of change at a specific point like x = 2, follow the same steps used to find the general derivative, but then substitute x with the specific value (in this case, 2) into the final simplified derivative formula to get the instantaneous rate of change at that point.
What are marginals in the context of revenue and cost functions?
-Marginals refer to the additional amount of revenue, cost, or profit associated with the production or sale of one more item, specifically the next one. If the revenue function is linear, the marginal revenue is constant and equals the slope of the function. If not, the marginal revenue at any point or a specific point is found by taking the derivative of the revenue function at that point.
How is the derivative of a function at a point related to the slope of the tangent line at that point?
-The derivative of a function at a point is equal to the slope of the tangent line at that point. It represents the instantaneous rate of change or the rate of change at that specific point.
What are the steps to find the equation of the tangent line to a function at a specific point?
-To find the equation of the tangent line, first determine the slope (m) of the tangent line, which is the derivative of the function at the given point. Then find the y-intercept (b) by plugging in the given x and y values from the point into the equation y = mx + b. Finally, use the values of m and b to write the equation of the line as y = mx + b.
What does the notation f'(x) or F(x) with an apostrophe represent in calculus?
-The notation f'(x) or F'(x) with an apostrophe represents the derivative of the function f(x) or F(x), which is the slope of the tangent line to the function at the point x.
Why is it important to understand the different ways to ask the same question when it comes to finding derivatives?
-Understanding the different ways to ask the same question about derivatives is important because it helps to recognize that various statements may all be asking for the same mathematical operation. This understanding prevents confusion and ensures that the correct process is applied to find the derivative.
Outlines
📐 Understanding Average and Instantaneous Rates of Change
This paragraph introduces the concept of average rates of change, which is the slope between two points, calculated as the rise over run or the difference in y values divided by the difference in x values. It connects this algebraic concept to the real-world application of velocity, which is the rate of change of position over time. The speaker encourages the audience to try a simple rate of change problem on their own before continuing. The paragraph then transitions into the topic of instantaneous rate of change, which is a more precise measure that uses the concept of a derivative. The derivative is explained as the limit of the difference quotient as the distance between points (h) approaches zero, providing the slope at a single point. The process of finding derivatives is outlined, including substituting x + h into the function, calculating the change in y values, forming the difference quotient, and applying the limit as h approaches zero.
📉 Derivatives and Marginal Analysis in Economics
The second paragraph delves into the application of derivatives in economics, specifically in the context of marginal analysis. It explains that marginals represent the additional revenue, cost, or profit associated with producing one more unit of a good. The paragraph clarifies that if revenue is a linear function, the marginal revenue is constant and equals the slope of the function. However, for non-linear functions, the marginal revenue at a specific point is found by taking the derivative at that point. The process of finding the derivative is reiterated, emphasizing that it involves finding the function for the second point, calculating the change in y values, forming the difference quotient, and applying the limit as h approaches zero. The paragraph concludes with an example of finding the instantaneous rate of change at a specific point x = 2, and how to solve for the equation of the tangent line given a point and the slope of the tangent.
🔍 Interpreting Different Requests for Derivatives
The final paragraph addresses the potential confusion arising from the multiple ways a question might ask for a derivative. It reassures the audience that despite the different phrasings, all such requests fundamentally seek the calculation of the derivative. The paragraph emphasizes that finding the derivative is a common task across various problems and reinforces the idea that a derivative represents the slope of the tangent line at a given point, which is a concept previously explored in algebra as the average rate of change between two points.
Mindmap
Keywords
💡average rate of change
💡velocity
💡units
💡derivative
💡limit
💡difference quotient
💡instantaneous rate of change
💡marginal cost
💡tangent line
💡linear function
💡Y-intercept
Highlights
The concept of average rate of change is introduced as the slope between two points, which is calculated as the rise over run or the difference in y values divided by the difference in x values.
Velocity is used as an example of a common rate of change, defined as the rate of change of position or distance over time.
The importance of including units in answers to word problems is emphasized, whether it's dollars, feet, or time.
Calculus is introduced as the study of instantaneous rate of change, which is found using the derivative, a new math concept.
The derivative is related to the difference quotient from algebra, with the addition of the concept of a limit as the difference (H) approaches zero.
The process of finding derivatives involves substituting x + H into the function, simplifying, and then applying the limit as H approaches zero.
The instantaneous rate of change at a specific point is found by plugging in the x value into the derivative formula.
Marginal revenue and cost are discussed in the context of linear and non-linear functions, and how derivatives can be used to find these at specific points.
The derivative at a point is identified as the slope of the tangent line at that point on the function's graph.
The process of finding the equation of the tangent line involves finding the slope (derivative) and the y-intercept using given points.
The derivative is denoted as F'(x) or f'(x) and represents the slope of the function f(x) at a given point x.
The equation of a line is given as Y = M * x + B, where M is the slope and B is the y-intercept.
The process of applying the limit to find the instantaneous rate of change is shown to bring two points closer together until they are the same, representing the slope at one point.
The concept of the difference quotient is used to calculate the change in y values and form the basis for the derivative.
The simplification process for finding the derivative involves factoring out terms and applying limits to simplify the expression.
The use of derivatives to find the marginal revenue at any point for non-linear functions is explained, highlighting their practical application in economics.
The transcript emphasizes the similarity between the concepts of average rate of change and instantaneous rate of change in calculus and their algebraic counterparts.
The final answer to a problem is demonstrated, showing the instantaneous change at x equals 3 to be 6, which is also the slope of the tangent line at that point.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: