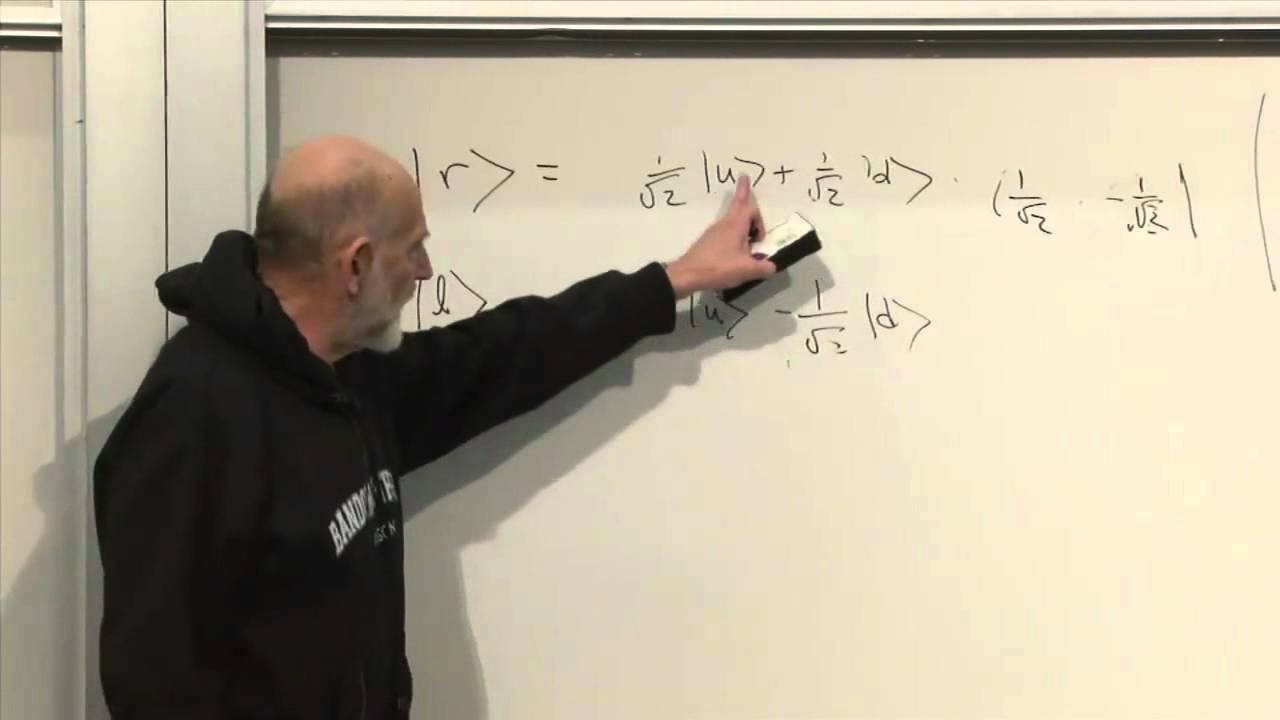Lecture 8 | New Revolutions in Particle Physics: Basic Concepts
TLDRThe video script is an in-depth exploration of quantum mechanics, specifically focusing on the concept of spin in particles. It delves into the mathematical framework of spin, starting from the basics of spin-half particles like electrons, which have two possible spin states. The lecturer discusses the representation of these states using two-component spinors and how operators become matrices in this space. The script then extends the discussion to spin-one particles, which are always bosons and have three possible states, using the Dirac equation to illustrate the connection between spin and the equation. The lecturer also touches on the implications of the Dirac equation, which predicts the existence of particles and antiparticles, such as electrons and positrons, as well as the concept of negative energy states and their role in defining the vacuum in quantum mechanics. The summary underscores the elegance of the mathematical descriptions and their profound physical implications, highlighting the predictive power of quantum theory and the deep connection between spin, statistics, and the behavior of particles at the subatomic level.
Takeaways
- 🚩 The script discusses the mathematical rules governing the behavior of bosons and fermions, highlighting the symmetry properties of their wave functions.
- 🌟 Bosons have wave functions that are symmetric upon interchange, meaning they can share the same quantum state, whereas fermions have wave functions that are antisymmetric and cannot share the same state.
- ⚖️ The Pauli Exclusion Principle is mentioned, which states that no two fermions can occupy the same quantum state simultaneously, leading to the concept of electron filling in atomic orbitals.
- 📉 The script touches on the creation of symmetric and antisymmetric wave functions from a given wave function, which is neither, by adding or subtracting the wave function upon interchange of particles.
- 🔴 The concept of isotopic spin (isospin) is introduced as a way to understand the symmetries of particle physics, drawing analogies between different types of conserved quantities.
- 🎓 The importance of understanding spin in quantum mechanics is emphasized, as it is fundamental to the mathematics of particle physics, including isospin and color charge in quantum chromodynamics.
- ⚙️ The script explains the commutation relations for spin operators and how they lead to the representation of spin states as eigenvectors of these operators.
- 🧲 The behavior of particles with spin one is explored, showing that they correspond to bosons and can be described by three-dimensional state spaces, in contrast to the two-dimensional spaces for spin half particles like electrons.
- 🚀 The Dirac equation is mentioned, which predicts the existence of particles and antiparticles, such as electrons and positrons, and is key to understanding the connection between quantum mechanics and special relativity.
- ✨ The script also delves into the concept of negative energy states and how they relate to the existence of antiparticles, such as positrons, formed as holes in a filled negative energy sea.
- ⛔ The annihilation process of electrons and positrons is discussed, explaining that it results in the emission of photons due to the conservation of energy.
- 🔬 The final part of the script invites further exploration of these concepts, suggesting that a deeper understanding comes from studying resources on the Dirac equation and its implications for particle physics.
Q & A
What is the fundamental principle behind the wave function of bosons?
-The wave function of bosons must be symmetric under interchange of the two particles. This means that the state of the system remains the same when you swap the positions of the two bosons, indicating that you cannot distinguish between them.
How does the wave function of fermions differ from that of bosons?
-The wave function of fermions, such as electrons, must change sign when you interchange the two particles. This is known as the Pauli Exclusion Principle, which states that no two fermions can occupy the same quantum state simultaneously.
What is the significance of the Pauli Exclusion Principle in quantum mechanics?
-The Pauli Exclusion Principle is significant because it dictates that no two fermions can share the same quantum state, which has profound implications for the structure of atoms and the behavior of electrons in orbitals.
How can you create a symmetric wave function from one that is neither symmetric nor anti-symmetric?
-To create a symmetric wave function, you can add the wave function with its variables interchanged. If you want to create an anti-symmetric wave function, you subtract the interchanged wave function from the original.
What is the concept of isotopic spin or isospin?
-Isotopic spin or isospin is a quantum number introduced to classify certain hadrons (particles composed of quarks) that share the same strong interactions. It is a form of spin that is not related to the intrinsic angular momentum of the particle but rather to its internal quantum state.
How does the Dirac equation relate to the concept of spin?
-The Dirac equation, which describes particles like electrons that have spin, incorporates the concept of spin through its algebraic structure. The equation predicts the existence of particles with both positive and negative energy and different spin states, which can be interpreted as electrons and positrons with spin up and spin down.
What is the role of the α (alpha) and β (beta) matrices in the Dirac equation?
-In the Dirac equation, the α matrices represent the orbital angular momentum of the electron, while the β matrix represents the rest energy of the electron. Together, they satisfy the anticommutation relations that define the algebraic structure of the equation.
Why are there four components to the Dirac spinor?
-The four components in the Dirac spinor correspond to the two possible energy states (positive and negative) and the two possible spin states (spin up and spin down) for particles like electrons.
How does the concept of spin relate to the conservation of angular momentum?
-Spin, as an intrinsic property of particles, contributes to the total angular momentum of a system. In any collision or scattering process, the total angular momentum, which includes the spin of the particles, is conserved.
What is the difference between a particle and an antiparticle?
-A particle and its corresponding antiparticle have the same mass but opposite charge. For example, an electron is a negatively charged particle, while a positron, its antiparticle, is positively charged. They also differ in their quantum spin states.
How does the zero momentum state simplify the Dirac equation?
-At zero momentum, the Dirac equation simplifies to a form where the α matrices can be ignored, and the equation describes the time evolution of the electron's wave function in terms of the β matrix and the electron's mass, revealing the particle's energy states.
Outlines
🎓 Understanding Bosons and Fermions
The paragraph discusses the paradox of identical particles, specifically bosons and fermions. It explains that bosons have symmetric wave functions, allowing multiple particles to occupy the same state. In contrast, fermions have antisymmetric wave functions, which means no two fermions can share the same quantum state. The script explores the mathematical representation of these properties and the implications for particle states.
🧬 Symmetrization and Anti-Symmetrization of Wave Functions
This section delves into the process of creating symmetric or antisymmetric wave functions for a system of two particles. It explains how to manipulate wave functions to adhere to the rules of bosons and fermions. The paragraph also touches on the concept of applying these rules to more complex systems, such as four-particle systems, and the importance of the wave function's behavior under particle interchange.
🚫 The Pauli Exclusion Principle and Quantum States
The focus here is on the Pauli Exclusion Principle, which states that no two fermions can occupy the same quantum state. The paragraph explores what happens when you try to place two atoms in the same momentum state and discusses the energy implications. It also differentiates between the inability to place two objects in the same spatial location and the quantum mechanical restrictions that fermions face.
🤔 The Paradox of Bosonic Atoms in the Same State
This section ponders the peculiar case of two bosonic atoms in the same state. It questions the conditions under which this can occur and what it implies for the electrons and protons within the atoms. The discussion highlights the importance of the wave function's symmetry and the probabilistic nature of particle positions in quantum mechanics.
🌀 The Mathematics of Spin
The paragraph introduces the mathematical treatment of spin, a fundamental property of particles. It emphasizes the importance of understanding spin to grasp other symmetries in particle physics. The discussion covers the algebraic properties of spin operators and the representation of spin states as two-component vectors for half-spin particles like electrons.
🔄 Spin Matrices and Their Representations
This section explores the spin matrices in more detail, focusing on their commutation relations and the conditions they must satisfy. It presents a specific set of 2x2 matrices that represent the spin operators for a half-spin particle. The paragraph also discusses the concept of raising and lowering operators for spin and the intrinsic nature of spin.
🧲 Spin States and Their Measurement
The paragraph discusses the concept of spin states and their measurement. It explains how to find the eigenvectors corresponding to the eigenvalues of spin matrices. The summary includes the process of determining the states for spin-up and spin-down along different axes, including the x, y, and z axes, and the superposition of these states.
🤹 Spin One Particles and Their Wave Functions
This section extends the discussion to spin one particles, which are always bosons. It explains that the wave function for a spin one particle is similar to that of a spin half particle but involves three components instead of two. The paragraph also covers how to calculate probabilities for different spin states and emphasizes the importance of understanding these probabilities in various positions.
🎛 The Dirac Equation and Its Implications
The paragraph introduces the Dirac Equation, which combines quantum mechanics and special relativity. It explains the equation's form and the conditions required for the matrices involved. The discussion highlights the prediction of particles with positive and negative energy and the concept of electron-positron pairs, which are key to understanding antimatter.
🧬 Spin, Statistics, and the Dirac Equation
This section connects the concepts of spin and statistics to the Dirac Equation. It explains how the equation predicts the existence of particles with specific spin properties and how these properties relate to the particle's statistics, such as bosons and fermions. The summary also touches on the conservation laws that govern particle interactions and the role of spin in these processes.
📚 Further Exploration of the Dirac Equation
The paragraph encourages further study of the Dirac Equation, suggesting that it is a rich topic that offers deep insights into the nature of particles and their interactions. It hints at the complexity of the equation and the profound implications it has for our understanding of the quantum world, including the behavior of electrons and positrons.
📅 Upcoming Schedule and Further Discussions
The final paragraph provides information about the upcoming schedule for further discussions and meetings. It assures the continuation of the exploration into the topics covered and thanks the participants for their patience and engagement in the complex subject matter.
Mindmap
Keywords
💡Bosons
💡Fermions
💡Wave Function
💡Quantum State
💡Symmetric and Anti-symmetric Wave Functions
💡Spin
💡
💡Pauli Exclusion Principle
💡Dirac Equation
💡Isospin
💡Quantum Superposition
💡Conservation Laws
Highlights
Exploration of the Paradox of identical particles, specifically bosons, and their wave function symmetry.
Discussion on the interchange symmetry of bosons and the mathematical rule involving the wave function of two bosons.
Explanation of how two bosons can share the same quantum state, demonstrated through a product wave function.
Contrasting bosons with fermions, highlighting the wave function's sign change when two fermions are interchanged.
Procedure to create symmetric or antisymmetric wave functions from a given wave function that is neither.
Analysis of the four-particle system, focusing on fermions and the Pauli Exclusion Principle.
Construction of a wave function for a hydrogen atom, considering the indistinguishability of electrons and protons.
Implications of the Pauli Exclusion Principle on the spatial arrangement of fermions.
Discussion on the possibility of two atoms sharing the same momentum state without being in the same position.
Introduction to the concept of spin in quantum mechanics and its importance in particle physics.
Mathematical treatment of spin using the Dirac equation, revealing the connection between spin and the particle's wave function.
Explanation of the spin matrices for half-spin particles like electrons and their role in quantum state descriptions.
Derivation of state vectors for spin-one particles and their interpretation in terms of probability amplitudes.
Correlation between the components of the Dirac equation and the physical properties of particles, such as energy and spin.
Prediction of the Dirac equation regarding the existence of positrons as the antiparticles of electrons.
Detailed examination of the Dirac equation for particles at rest, leading to the understanding of positive and negative energy states.
Insight into the vacuum state being filled with negative energy electrons, and the concept of electron-positron annihilation.
Discussion on the stability of positrons and the conditions under which an electron can change its energy by emitting photons.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: