Meaning of P-value and Alpha
TLDRThe video script offers a clear explanation of the concepts of p-value and alpha in statistical hypothesis testing. It emphasizes the difference between the two, with the p-value being the probability of obtaining a test value as extreme as the one calculated, assuming the null hypothesis is true. This is represented by the area under the curve to the right of the test value. On the other hand, the alpha level is the threshold set by the researcher to determine statistical significance, and it represents the probability of rejecting the null hypothesis when it is actually true, known as a type one error. The critical value, which is derived from statistical charts, corresponds to the alpha level. The script also touches on the concept of a two-tailed test, where both tails are considered. Understanding these concepts is crucial for researchers aiming to minimize the risk of making incorrect conclusions in their studies.
Takeaways
- 📊 **P-value Definition**: The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one calculated from my sample data, assuming the null hypothesis is true.
- 🔍 **P-value Location**: The p-value is associated with the test statistic on the horizontal axis, which could be a z, t, or chi-squared distribution.
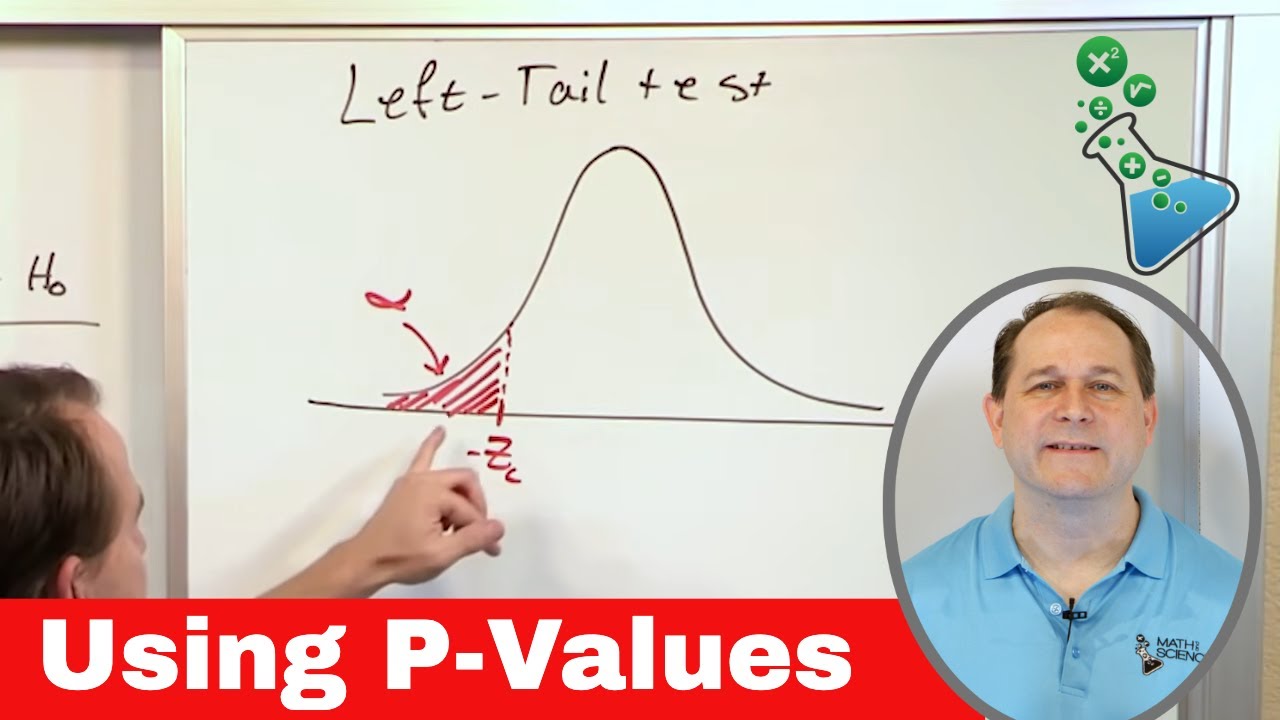
- 🟥 **Area of P-value**: The p-value represents the area to the right of the test statistic under the curve of the distribution (the red area in the transcript).
- 📉 **Critical Value**: A critical value is a threshold that comes from statistical charts, not from formulas, and it is used to determine the rejection of the null hypothesis.
- 🔴 **Alpha (α)**: Alpha is the probability of rejecting the null hypothesis when it is actually true. It is the area to the right of the critical value in a right-tailed test.
- 📍 **Null Hypothesis**: The null hypothesis (H0) typically states that there is no difference or no effect, and it is what we compare our sample data against.
- 🚫 **Type I Error**: A type I error occurs when the null hypothesis is true, but it is incorrectly rejected. The probability of this error is represented by alpha.
- 🔢 **Setting Alpha**: Researchers can set their alpha level, for example, at 0.01, to control the risk of making a type I error to 1%.
- 🔄 **Two-Tailed Test**: In a two-tailed test, we consider the area in both tails of the distribution, looking at both extremes rather than just one.
- 🔵 **Area Under the Curve**: The area under the curve in a statistical distribution represents probabilities, which is a fundamental concept in understanding p-values and alpha levels.
- ⚖️ **Balance of Error Types**: There is a balance between type I and type II errors in hypothesis testing, where lowering the risk of one may increase the risk of the other.
- 🧮 **Statistical Decision Making**: The decision to reject or not reject the null hypothesis is based on whether the p-value is less than or equal to the alpha level.
Q & A
What is the p-value and how is it represented on a statistical test?
-The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one calculated from my sample data, assuming that the null hypothesis is true. It is represented on the horizontal axis of a statistical distribution, such as the Z, T, or chi-squared axis.
What does the area to the right of the test value on a statistical graph represent?
-The area to the right of the test value represents the p-value, which is the probability of getting a test value at that line or more to the right.
What is the critical value in statistical testing and where does it come from?
-The critical value is a threshold value determined by a statistical model that separates the region of non-rejection of the null hypothesis from the region of rejection. It is derived from statistical charts, not formulas, and can be a Z, T, or chi-squared value depending on the test being used.
What is the area to the right of the critical value called in a right-tailed test?
-In a right-tailed test, the area to the right of the critical value is called alpha.
What is the relationship between alpha and the probability of committing a Type I error?
-Alpha represents the probability of committing a Type I error, which is the error of rejecting a true null hypothesis. It is the threshold probability for deciding to reject the null hypothesis when it is actually true.
How does the null hypothesis relate to the concept of 'no change' or 'no difference'?
-The null hypothesis typically represents a default position that there is no change or no difference between the groups or variables being compared. It usually states that any observed differences are due to random chance.
What is a Type I error in the context of hypothesis testing?
-A Type I error occurs when the null hypothesis is true, but it is incorrectly rejected. It is the mistake of concluding that there is an effect or a difference when there is none.
Why would a researcher set their alpha value at 0.01?
-A researcher might set their alpha value at 0.01 to ensure that there is only a 1% chance of making a Type I error, which is rejecting the null hypothesis when it is actually true.
What does it mean if the p-value is less than the alpha level?
-If the p-value is less than the alpha level, it suggests that the observed data is unlikely to have occurred by chance alone, given the null hypothesis, leading to the rejection of the null hypothesis.
How does a two-tailed test differ from a one-tailed test in terms of the alpha level?
-In a two-tailed test, the alpha level is split between the two tails of the distribution (left and right), whereas in a one-tailed test, the entire alpha level is allocated to one tail (either left or right), making it more sensitive to detecting an effect in that direction.
What is the significance of the horizontal axis in the context of statistical tests?
-The horizontal axis in statistical tests represents the range of possible values that a test statistic can take. It is used to plot the distribution of the test statistic and to determine the p-value and critical values.
Can you explain the concept of the null hypothesis in simple terms?
-The null hypothesis is a statement that there is no significant difference or effect to be measured. It is a starting point for statistical testing, and researchers try to find evidence against it to support an alternative hypothesis.
Outlines
📊 Understanding P-value and Alpha
The paragraph explains the fundamental difference between a p-value and alpha in statistical testing. A p-value is the probability of obtaining a test value as extreme as the one calculated, assuming the null hypothesis is true. It's derived from statistical formulas and can be represented on a Z, T, or chi-squared distribution axis. The alpha level, on the other hand, is the threshold for rejecting the null hypothesis and is determined by looking at the area to the right of a critical value on the same distribution axis. It's the probability of making a Type I error, which is the incorrect rejection of a true null hypothesis. The speaker also discusses setting the alpha level to control the risk of Type I error, such as setting it at 0.01 for a 1% chance of such an error.
Mindmap
Keywords
💡p-value
💡alpha
💡test statistic
💡null hypothesis
💡critical value
💡Type I error
💡hypothesis testing
💡probability
💡Z-test
💡T-test
💡chi-squared test
💡F-test
Highlights
The difference between p-value and alpha is explained in detail.
A p-value is the probability of getting the test value or a more extreme test value if the null hypothesis is true.
The p-value is associated with the area under the curve to the right of the test value on the horizontal axis.
Critical values are derived from charts, not formulas, and are represented by Z, T, or chi-squared values.
Alpha is the area to the right of the critical value in a right-tailed test.
In a two-tailed test, the focus is on both tails of the distribution.
Alpha represents the probability of rejecting the null hypothesis when it is actually true.
The null hypothesis typically states there is no change or difference between the variables being studied.
Type I error occurs when the null hypothesis is true, but it is incorrectly rejected.
The probability of a Type I error is denoted by alpha.
Researchers can set their alpha level to control the risk of a Type I error, such as setting it at 0.01 for a 1% chance.
The null hypothesis is often positioned in the middle, indicating no difference or equality between the variables.
Understanding the concepts of p-value and alpha is crucial for hypothesis testing in statistics.
Setting an appropriate alpha level ensures the balance between avoiding false positives and detecting true effects.
The transcript provides a clear explanation of statistical terms that are fundamental to hypothesis testing.
The importance of correctly interpreting p-values and alpha levels in the context of statistical significance is emphasized.
The transcript offers practical advice on how to set alpha levels based on the desired risk of Type I error.
The discussion clarifies the role of the null hypothesis in statistical analysis and its relationship with p-values and alpha.
Transcripts
Browse More Related Video

What is p-value? How we decide on our confidence level.

Introduction to Type I and Type II errors | AP Statistics | Khan Academy
05 - Using P-Values in Hypothesis Testing (Compare P Value to Level of Significance)

p-value - easily explained with an example

p-Value (Statistics made simple)

Type 1 errors | Inferential statistics | Probability and Statistics | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: