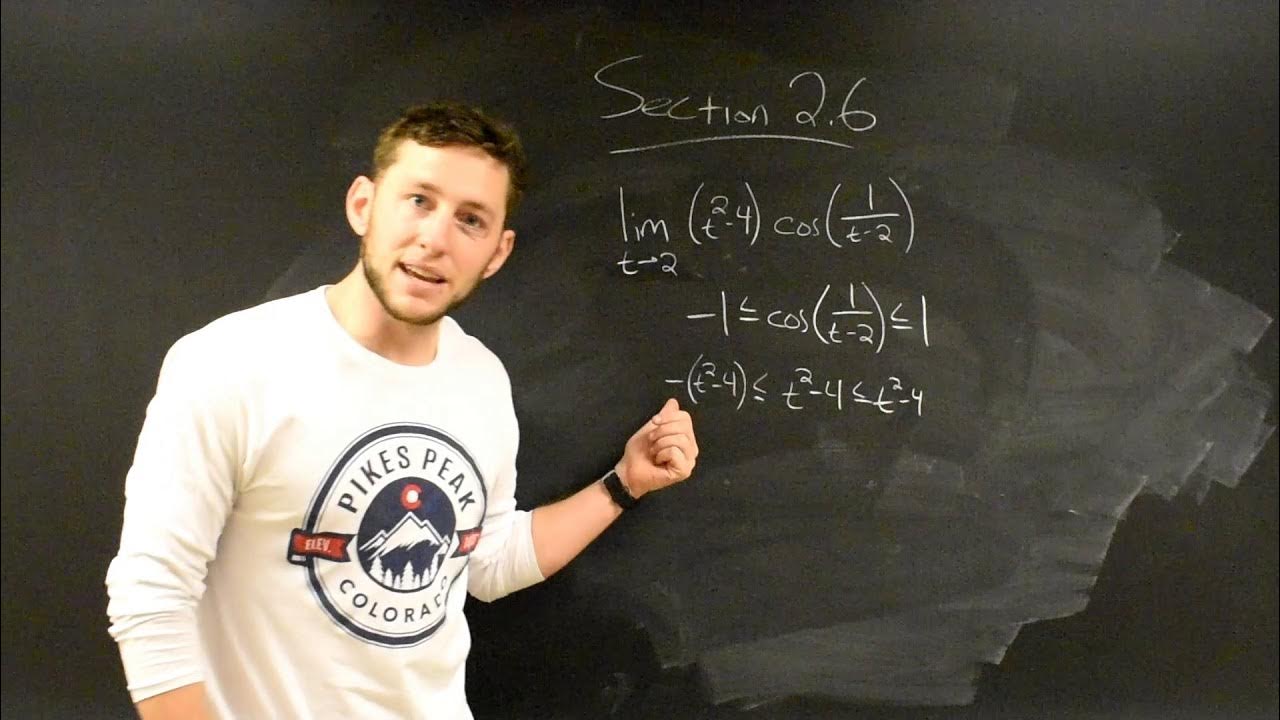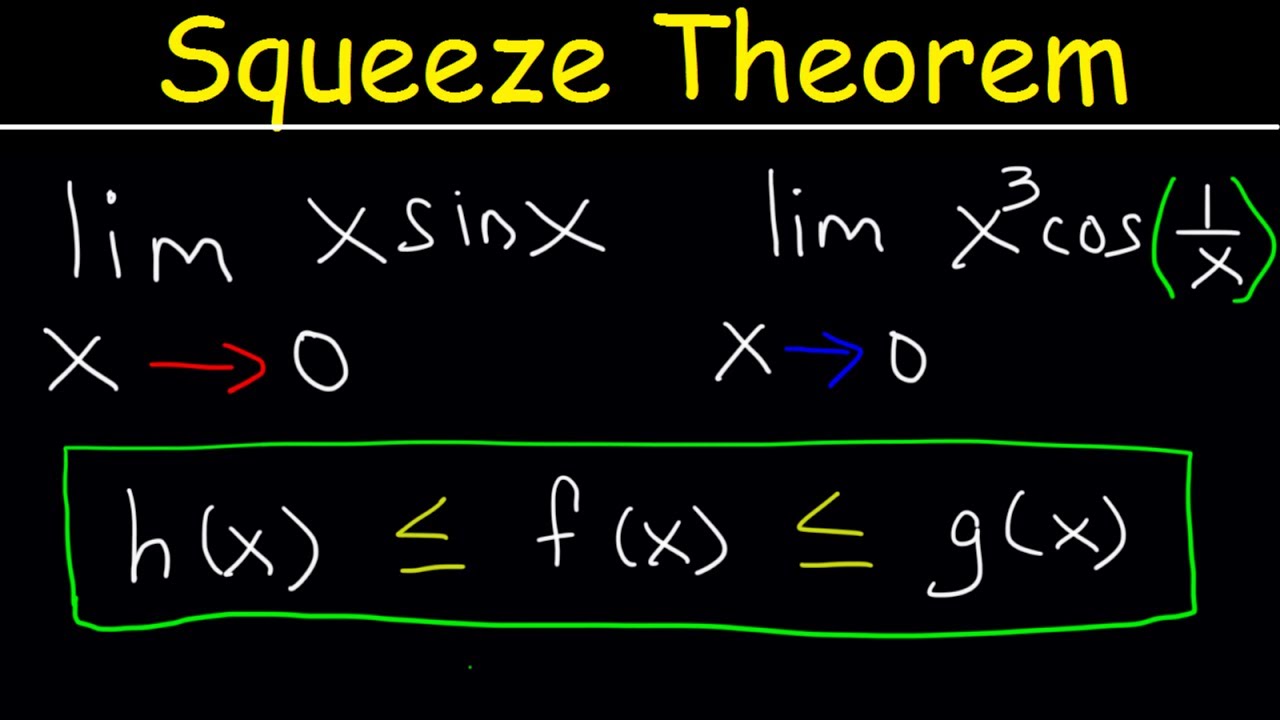SQUEEZE THEOREM - The Setup
TLDRThis video provides a comprehensive explanation of the Squeeze Theorem, a mathematical concept used to solve limit problems when direct methods are not applicable. The presenter begins by defining the theorem, explaining that it involves establishing an inequality with a function or expression sandwiched between a lower and upper boundary. The video then delves into a step-by-step application of the theorem to a specific limit problem involving polynomials and trigonometric functions. The presenter emphasizes the importance of recognizing the boundaries of trigonometric functions like cosine, which is bounded between -1 and 1. The solution process involves manipulating the given expression to fit the theorem's criteria, adding terms, and then dividing by (x^2 - 7). The crux of the video is the application of limits to the manipulated expressions, leveraging the knowledge of horizontal asymptotes to find that the limit of the expression as x approaches negative infinity is 4. The video concludes by reiterating the theorem's utility in solving limit problems and encourages continuous learning.
Takeaways
- 📚 The Squeeze Theorem is a mathematical tool used to find limits when direct methods are not applicable or when the problem specifically requires its use.
- 📌 The theorem states that if F(x) <= G(x) <= H(x) and F(x) = H(x) at a certain point, then G(x) must equal both F(x) and H(x), meaning no gap can exist between a number and itself.
- 🔢 To apply the Squeeze Theorem, establish an inequality with known bounds, where the function or expression of interest lies between these bounds.
- 📈 Polynomials like x^2 and x^2 - 7 increase without limit, which is a key consideration when evaluating their behavior as x approaches infinity.
- 📊 Trigonometric functions, specifically cosine, are bounded between -1 and 1, making them ideal candidates for the Squeeze Theorem when dealing with limits involving trigonometric expressions.
- 🚫 Tangent functions are not suitable for the Squeeze Theorem as they can extend to positive and negative infinity, thus not providing a bounded interval.
- ➗ When multiplying or dividing by a negative constant in an inequality, the direction of the inequality sign must be reversed.
- 🔄 To apply the Squeeze Theorem, rewrite the expression to resemble the bounds and then manipulate algebraically to fit the theorem's criteria.
- 🔢 The limit of a rational function as x approaches infinity or negative infinity can often be found by considering the highest power of x in the denominator, as other terms become insignificant.
- 🎯 The horizontal asymptote of a rational function is the value that the limit of the function approaches as x goes to positive or negative infinity, which is a key concept in applying the Squeeze Theorem.
- 🏁 The final step is to take the limit as x approaches the specified value (in this case, negative infinity) and compare the results from the bounds to determine the limit of the expression of interest.
Q & A
What is the Squeeze Theorem?
-The Squeeze Theorem is a mathematical theorem used to find the limit of a function when it is difficult to calculate directly. It states that if a function f(x) is bounded between two other functions g(x) and h(x), and if g(x) and h(x) have the same limit at a certain point, then f(x) must also have that limit at that point.
Why is it necessary to establish an inequality when using the Squeeze Theorem?
-An inequality is necessary because the Squeeze Theorem requires a lower boundary (g(x)) and an upper boundary (h(x)) that 'squeeze' the function f(x) in between them. The function f(x) must be less than or equal to the upper boundary and greater than or equal to the lower boundary for the theorem to apply.
How does the behavior of a polynomial function like x^2 affect its limit as x approaches infinity?
-A polynomial function like x^2 is unbounded, meaning it has no limit as x approaches infinity. The value of x^2 will keep increasing without bound, regardless of the value of x.
What is the range of the cosine function, and how does it relate to the Squeeze Theorem?
-The cosine function has a range of [-1, 1], meaning its values are always between -1 and 1, inclusive. This property is useful in the Squeeze Theorem because it provides a clear upper and lower boundary for the function when dealing with trigonometric limits.
Why is it important to consider the behavior of the denominator when taking the limit of a rational function as x approaches infinity?
-When taking the limit of a rational function as x approaches infinity, the behavior of the denominator is crucial because it determines the horizontal asymptote of the function. The highest power of x in the denominator will dominate the behavior of the function as x becomes very large.
How does the sign change when you multiply or divide by a negative constant in an inequality?
-When you multiply or divide both sides of an inequality by a negative constant, the direction of the inequality sign must be reversed. This is a basic principle of algebra that ensures the inequality remains true after the operation.
What is the significance of adding 4x^2 to both sides of an inequality when applying the Squeeze Theorem?
-Adding 4x^2 to both sides of an inequality is a step to create a new expression that still maintains the inequality's relationship but is closer in form to the original function you are trying to evaluate. This is a common technique used to facilitate the application of the Squeeze Theorem.
What is the assumption made when dividing by x^2 - 7 in the context of the Squeeze Theorem?
-The assumption is that x^2 - 7 will be positive as x approaches negative infinity. This is because x^2 will grow larger in magnitude as x moves away from zero, making the negative seven insignificant compared to x^2.
Why is it stated that the limit of 4x^2/x^2 as x approaches infinity is 4?
-The limit of 4x^2/x^2 as x approaches infinity is 4 because the highest power of x in both the numerator and the denominator is x^2. As x becomes very large, the x^2 terms cancel each other out, leaving you with the constant term 4.
How does the Squeeze Theorem help in finding the limit of a function that is not directly solvable?
-The Squeeze Theorem helps by allowing you to find the limit of a function by bounding it between two other functions whose limits are known or easier to find. If the limits of the bounding functions are the same, then the limit of the function in question must also be that value.
What is the final conclusion of the limit as x approaches negative infinity for the given function in the script?
-The final conclusion is that the limit as x approaches negative infinity of the function 4x^2 - cos(5x) / (x^2 - 7) is equal to 4. This is determined by applying the Squeeze Theorem and finding that the function is 'squeezed' between two expressions that both approach 4 as x approaches negative infinity.
Outlines
📘 Introduction to Squeeze Theorem
The first paragraph introduces the concept of the Squeeze Theorem, which is a method for finding limits of functions. It explains that if a function is 'squeezed' between two others and meets at a point, then the middle function must equal the others at that point. The paragraph also emphasizes the need to establish an inequality to apply the theorem and discusses the behavior of polynomials and trigonometric functions in relation to the theorem.
🔍 Applying Squeeze Theorem to a Specific Problem
The second paragraph delves into the application of the Squeeze Theorem to a specific mathematical problem involving polynomials and trigonometric functions. It outlines the steps to manipulate the given expression to fit the theorem's criteria, including rewriting the expression with appropriate boundaries and expanding it to match the form required for the theorem. The paragraph also touches on the behavior of cosine function and how it is bounded, which is crucial for the application of the Squeeze Theorem.
🏁 Conclusion and Final Limit Calculation
The third paragraph concludes the application of the Squeeze Theorem by calculating the limit as X approaches negative infinity for the given expression. It demonstrates how to find the horizontal asymptote of a rational expression, which is key to determining the limit. The paragraph reinforces the idea that the limit of the middle expression is 'squeezed' between two constants, leading to the conclusion that the limit is 4. The video ends with an encouragement to continue learning and a prompt for viewers to like, share, and subscribe.
Mindmap
Keywords
💡Squeeze Theorem
💡Limit
💡Polynomial
💡Trigonometric Function
💡Horizontal Asymptote
💡Inequality
💡Cosine Function
💡Negative Infinity
💡Rational Expression
💡Asymptote
💡Multiplication by a Negative Constant
Highlights
The Squeeze Theorem is a specific method used to solve limit problems when the question mandates its use.
The theorem states that if f(x) ≤ g(x) ≤ h(x) and f(x) = h(x) at a certain point, then g(x) must equal both of them.
The concept of the Squeeze Theorem is to establish an inequality with a lower and upper boundary, with the function in the middle.
For polynomials, the function can increase without limit, making it necessary to find a way to apply the Squeeze Theorem.
The trigonometric function cosine is bounded between -1 and 1, making it a good candidate for setting boundaries in the Squeeze Theorem.
The expression within the Squeeze Theorem must be manipulated to resemble an inequality with clear upper and lower bounds.
Multiplying or dividing by a negative constant requires flipping the inequality signs.
When applying the Squeeze Theorem, it's important to consider the behavior of the function as x approaches the limit.
The limit of a rational expression as x approaches infinity or negative infinity can often be found by considering the highest power of x in the denominator.
The horizontal asymptote of a rational expression is the same as the limit as x approaches positive or negative infinity.
In the given example, the limit as x approaches negative infinity of the expression is found to be 4, by applying the Squeeze Theorem.
The Squeeze Theorem can be applied to trigonometric functions like cosine, which have a bounded range.
The process of applying the Squeeze Theorem involves rewriting expressions to fit the theorem's criteria and then taking the limit.
The final answer obtained from applying the Squeeze Theorem is the same as the limit of the middle expression, provided the limits of the outer expressions are equal.
The video provides a step-by-step guide on how to apply the Squeeze Theorem to a limit problem involving a polynomial and a trigonometric function.
The Squeeze Theorem is a powerful tool for solving limit problems when direct substitution or other methods are not applicable.
The video concludes with the reminder that the limit of the middle expression, when squeezed by two equal limits, must also be equal to that value.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: