Polar coordinates 1 | Parametric equations and polar coordinates | Precalculus | Khan Academy
TLDRThe video script introduces the concept of Cartesian coordinates, which are used to specify a point in two-dimensional space by its distance from the origin along the x and y axes. It explains that while Cartesian coordinates are common, another method of specifying a point is through polar coordinates, which use a distance from the origin (r) and an angle (theta). The script demonstrates how to convert between Cartesian and polar coordinates using the Pythagorean theorem and trigonometric functions, specifically tangent, sine, and cosine. It also highlights the mnemonic SOHCAHTOA to help remember the relationships between the trigonometric functions and the sides of a right triangle. The process of converting a point from Cartesian (x, y) to polar (r, theta) and vice versa is outlined, with examples provided to illustrate the calculations involved.
Takeaways
- 📐 Cartesian coordinates are a system for specifying points in a plane using x and y directions.
- 📈 The script introduces the concept of Cartesian coordinates, which can be applied to more than just 2 dimensions, but primarily focuses on 2D.
- 👉 To determine a point in 2D space using Cartesian coordinates, one needs to know the distance in the x-direction and the y-direction from the origin.
- 📍 An example of Cartesian coordinates is given as (3, 4), where '3' is the distance along the x-axis and '4' is the distance along the y-axis.
- 🔄 It's noted that reaching a point can be achieved by moving in any order along the x and y axes, the result will be the same.
- 🧭 An alternative to Cartesian coordinates is specifying a point by direction and distance, using polar coordinates (r, θ).
- 🌐 Polar coordinates are defined by a radius (r) and an angle (θ) from the x-axis, indicating the direction to walk.
- 📚 The script explains the conversion from Cartesian to polar coordinates using the Pythagorean theorem and trigonometric identities.
- 📉 The Pythagorean theorem is used to find the radius (r) of the polar coordinates, by calculating the square root of the sum of the squares of the x and y coordinates.
- 📌 The tangent function (SOHCAHTOA) is used to find the angle (θ) by taking the inverse tangent of the ratio of the y-coordinate to the x-coordinate.
- 🔢 The script provides a practical demonstration of calculating the angle θ using a calculator, resulting in 53.13 degrees for the given example.
- 🔄 The conversion formulas x = r * cos(θ) and y = r * sin(θ) are derived, which allow for the translation between polar and Cartesian coordinates.
Q & A
What are Cartesian coordinates?
-Cartesian coordinates are a system used to specify points in a two-dimensional plane by stating how far one must go in the x-direction and y-direction from a reference point, typically the origin.
How many dimensions can Cartesian coordinates apply to?
-While Cartesian coordinates are commonly used in two dimensions, they can be extended to three or more dimensions.
What is the convention for naming the coordinates in a Cartesian system?
-By convention, the first coordinate is the x-coordinate, which represents the horizontal distance from the origin, and the second coordinate is the y-coordinate, which represents the vertical distance.
Can you reach the same point by moving in a different order in the Cartesian coordinate system?
-Yes, you can reach the same point by moving in a different order, such as going 3 units to the right and then 4 units up, or vice versa.
What is an alternative way to specify a point in a plane besides Cartesian coordinates?
-An alternative method is to specify a point using polar coordinates, which involve giving a direction (measured in degrees or radians) and a distance from the origin.
How can you convert between degrees and radians when dealing with polar coordinates?
-Radians are the standard unit in polar coordinates. To convert from degrees to radians, multiply the degree measure by π/180. To convert from radians to degrees, multiply the radian measure by 180/π.
What is the Pythagorean theorem and how is it used in the context of polar coordinates?
-The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (r) is equal to the sum of the squares of the lengths of the other two sides (x and y). In polar coordinates, it's used to find the radial distance r from the Cartesian coordinates (x, y) using the formula r^2 = x^2 + y^2.
What trigonometric function is used to find the angle theta in polar coordinates?
-The tangent function is used to find the angle theta in polar coordinates. It is calculated as the ratio of the opposite side (y-coordinate) to the adjacent side (x-coordinate), or tan(theta) = y/x.
How do you find the angle theta if you know the Cartesian coordinates (x, y)?
-To find the angle theta, you calculate the tangent of theta as y/x and then take the inverse tangent (arctan) of that value, which can be done using a calculator set to the appropriate mode (degrees or radians).
What are the formulas to convert from Cartesian coordinates (x, y) to polar coordinates (r, theta)?
-To convert to polar coordinates, use the formulas r = sqrt(x^2 + y^2) and theta = arctan(y/x). These formulas allow you to find the radial distance and the angle from the origin to the point (x, y).
How can you express y and x in terms of r and theta using trigonometric identities?
-You can express y as y = r * sin(theta) and x as x = r * cos(theta). These expressions come from the definitions of sine and cosine in a right triangle, where r is the hypotenuse, y is the opposite side for sine, and x is the adjacent side for cosine.
Outlines
📏 Introduction to Cartesian Coordinates
This paragraph introduces the concept of Cartesian coordinates in a two-dimensional space. It explains that Cartesian coordinates are a way to specify a point by stating the distance in the x-direction and the y-direction from the origin. The speaker uses the example of a point located 3 units to the right and 4 units up from the origin, which is denoted as (3, 4). The paragraph also touches on the idea of specifying a point by direction and distance, which is a precursor to polar coordinates, and sets the stage for the transition from Cartesian to polar coordinate systems.
📐 Transition from Cartesian to Polar Coordinates
The second paragraph delves into the transition from Cartesian to polar coordinates. It explains that polar coordinates are another way to specify a point in a plane, using a distance from the origin (r) and an angle (theta) from the x-axis. The speaker uses the Pythagorean theorem to show how to calculate r from the Cartesian coordinates (x, y), resulting in r = √(x² + y²). The tangent of theta is then found using the ratio of the y-coordinate to the x-coordinate, which is tan(theta) = y/x. The paragraph concludes with the calculation of theta using the arctan function on a calculator, yielding theta = arctan(4/3) ≈ 53.13 degrees. This establishes the polar coordinates as (r, theta) for the example point.
🔍 General Formulas for Polar and Cartesian Coordinate Conversion
The final paragraph provides general formulas for converting between polar and Cartesian coordinates. It reiterates the formulas derived in the previous paragraph: r = √(x² + y²) for finding the radial distance from the origin, and tan(theta) = y/x for determining the angle from the x-axis. Additionally, it introduces the reverse relationships: y = r * sin(theta) and x = r * cos(theta), which allow for the conversion from polar back to Cartesian coordinates. The paragraph emphasizes the importance of these formulas, as they equip the viewer with the tools to convert between the two coordinate systems, setting the stage for further exploration in the next video.
Mindmap
Keywords
💡Cartesian coordinates
💡x-axis and y-axis
💡Polar coordinates
💡Degrees and radians
💡Trigonometry
💡Pythagorean theorem
💡Tangent
💡Inverse tangent (arctan)
💡SOHCAHTOA
💡Conversion between polar and rectangular coordinates
Highlights
Introduction to Cartesian coordinates and their application in more than just 2 dimensions.
Explanation of how to specify a point in 2D space using x and y directions.
Convention of naming coordinates as x and y, and representing them as ordered pairs.
Illustration of reaching the same point in 2D space by different paths.
Introduction of an alternative method to specify a point using direction and distance.
Use of degrees to specify direction on the x-axis and the concept of theta.
Conversion between degrees and radians for direction specification.
Introduction of polar coordinates as an alternative to Cartesian coordinates.
Explanation of polar coordinates using r (radius) and theta (angle).
Demonstration of calculating r using the Pythagorean theorem.
Use of trigonometry to find theta, specifically the tangent function.
Calculation of theta using the arctangent function.
Practical example of converting Cartesian coordinates (3,4) to polar coordinates (r=5, theta=53.13 degrees).
General formulas for converting between Cartesian (x, y) and polar (r, theta) coordinates.
Derivation of the formula r = sqrt(x^2 + y^2) for converting to polar coordinates.
Derivation of the formula theta = arctan(y/x) for converting to polar coordinates.
Explanation of how to convert back from polar to Cartesian using trigonometric identities.
Formulas x = r * cos(theta) and y = r * sin(theta) for converting from polar to Cartesian coordinates.
Emphasis on the importance of understanding trigonometric identities for coordinate conversion.
Transcripts
Browse More Related Video

Polar Coordinate System | Physics with Professor Matt Anderson | M3-02

Lesson 14 - Polar Equations (Calculus 2 Tutor)

Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy

An Example Using Polar Coordinates | Physics with Professor Matt Anderson | M3-09
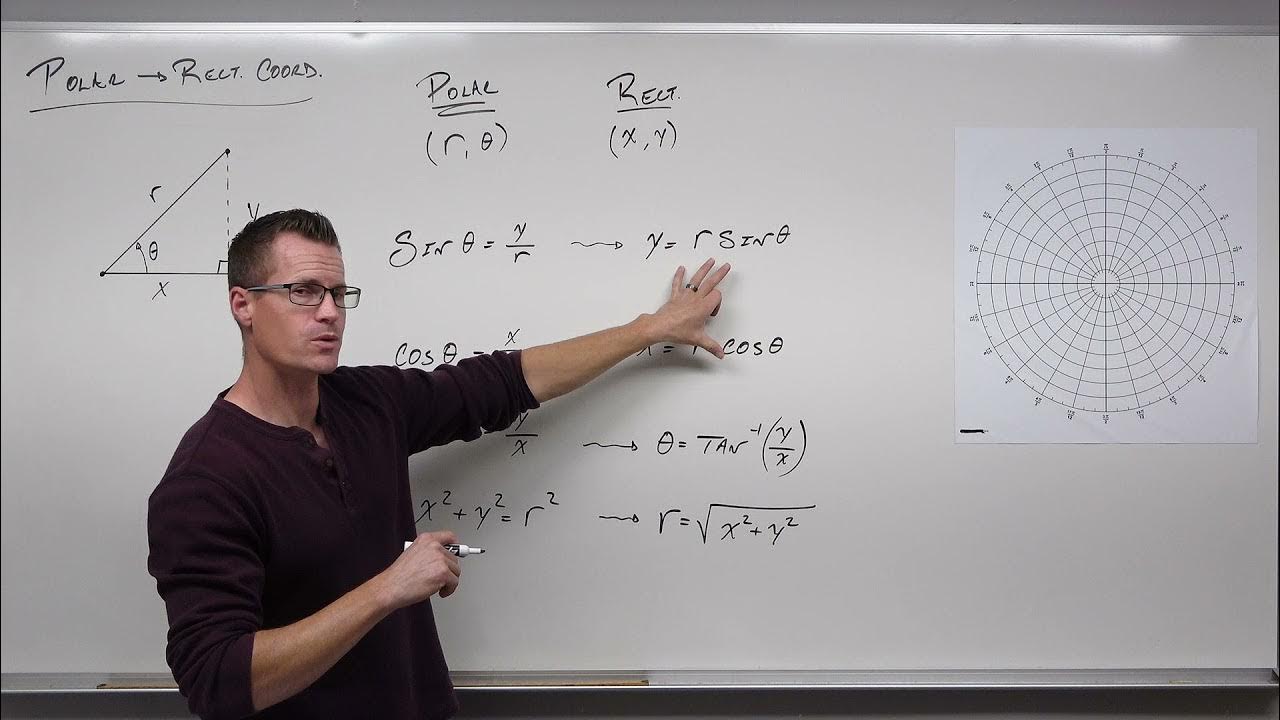
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

Polar coordinates 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: