Power Formula - Worked Example 1

Sparky Help
3 Apr 202009:31
EducationalLearning
32 Likes 10 Comments

TLDRThe video script introduces three fundamental electrical power formulas, highlighting their applications in calculating power in both AC and DC circuits. It begins with the basic formula, Power = V*I, and extends it to include Ohm's Law, resulting in two additional formulas: Power = V^2/R and Power = I^2*R. The script then demonstrates their use in a series circuit with a 100-volt supply, showing how each formula can be applied to find the total power consumption. The explanation emphasizes the importance of understanding these formulas for electrical engineering and problem-solving, and it clarifies which formulas apply to specific types of circuits.

Takeaways
  • πŸ”Œ Basic Power Formula: Power (P) equals Voltage (V) times Current (I), measured in watts, which is universally applicable and helpful in various electrical scenarios.
  • πŸ“ Ohm's Law Application: Power can also be expressed as P times I, derived from Ohm's law (V=I*R), leading to the formula P=V^2/R for resistive loads.
  • πŸ”„ Power in AC and DC Circuits: The formula P=V*I is applicable to both AC and DC circuits, while P=I^2*R is specific to resistive loads and works for both AC and DC.
  • πŸ”© Circuit Analysis: In a series circuit with R1 and R2, the total voltage supply can be analyzed using the power formulas, regardless of whether it's AC or DC.
  • πŸ”’ Calculation of Total Current (IT): To find the total current, apply Ohm's law, which is IT = V_total / (R1 + R2), where V_total is the supplied voltage and R1 and R2 are the resistances in the circuit.
  • πŸ’‘ Power Calculation Examples: Using the derived formulas, the total power consumption of the circuit can be calculated as 200 watts using P=V*I, P=V^2/R, and P=I^2*R, assuming a 100-volt supply and a total resistance of 50 ohms.
  • πŸ” Importance of Understanding Formulas: Knowing the different power formulas is crucial for accurately calculating power in electrical circuits and for solving related problems.
  • πŸ“Œ Voltage and Current Relationship: The relationship between voltage, current, and power is fundamental in understanding how electrical energy is converted and utilized in a circuit.
  • πŸ”Ž Resistance Impact on Power: The power formulas highlight the impact of resistance on the power consumed or generated in a circuit, with P=I^2*R emphasizing the squaring effect of current.
  • πŸ“Š Power Formulas' Applicability: The script clarifies which power formulas are applicable to DC, AC, or both, aiding in selecting the correct formula for specific electrical scenarios.
  • πŸ”§ Practical Application: The formulas discussed are not only theoretical but also have practical applications, such as determining the current draw of household appliances like a shower.
Q & A

  • What is the basic power formula and what units are used for each component?

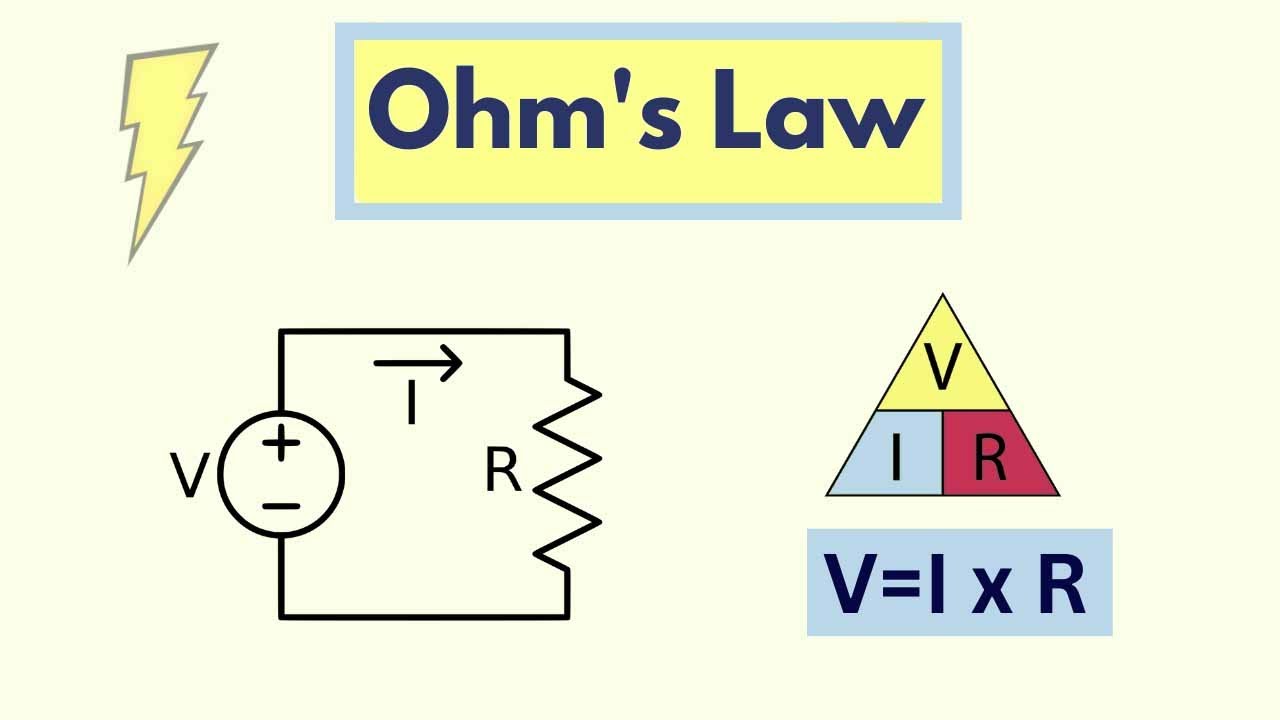
    -The basic power formula is P = V Γ— I, where P stands for power measured in watts, V is voltage measured in volts, and I is current measured in amps.

  • How can you find the current in a circuit using the power formula?

    -To find the current in a circuit, you can rearrange the power formula to I = P / V, where P is the power in watts and V is the voltage in volts.

  • What are the two other power formulas derived from Ohm's law?

    -The two other power formulas derived from Ohm's law are P = V^2 / R and P = I^2 Γ— R.

  • Which power formula is applicable to both AC and DC circuits?

    -The formula P = I^2 Γ— R can be used for both AC and DC circuits, while P = V^2 / R is applicable only to DC circuits.

  • How does Ohm's law relate to the power formulas?

    -Ohm's law, which states V = I Γ— R, is used to derive the power formulas by replacing current (I) or voltage (V) with the expression from Ohm's law in the basic power formula P = V Γ— I.

  • In the given script, what is the total voltage supply for the series circuit?

    -The total voltage supply for the series circuit mentioned in the script is 100 volts.

  • How is the total resistance in a series circuit calculated?

    -In a series circuit, the total resistance (RT) is calculated by adding the individual resistances together, i.e., RT = R1 + R2.

  • What is the current (IT) in the series circuit example provided?

    -In the series circuit example, the current (IT) is calculated as 100 volts divided by the total resistance of 50 ohms, resulting in IT = 2 amps.

  • How much power is consumed by the series circuit in the example?

    -The power consumed by the series circuit in the example is 200 watts, calculated using the formula P = V Γ— I (100 volts Γ— 2 amps).

  • What is the significance of knowing these power formulas in practical applications?

    -Knowing these power formulas is significant in practical applications as they help in calculating power consumption, designing electrical circuits, and troubleshooting electrical problems, such as determining how much current a shower would draw.

  • How can the power consumed by individual components in a circuit be calculated?

    -The power consumed by individual components can be calculated using the appropriate power formula, such as P = V Γ— I for the total power, or P = I^2 Γ— R for the power consumed by a resistor, by knowing the voltage, current, and resistance of each component.

Outlines
00:00
πŸ”Œ Fundamental Electrical Power Formulas

This paragraph introduces three fundamental formulas for calculating electrical power. The first formula is the basic power equation, P=V*I, where P is power in watts, V is voltage in volts, and I is current in amps. This formula is foundational and can be used in various scenarios, such as determining the current drawn by a shower. The other two formulas are derived from Ohm's law (V=I*R). The second formula is P=V^2/R, applicable to DC circuits, and the third is P=I^2*R, which works for both AC and DC circuits. The importance of understanding these formulas is emphasized, as they are essential for solving electrical problems and understanding power dynamics in circuits.

05:05
πŸ” Calculating Power in a Series Circuit

This paragraph delves into the application of the electrical power formulas in a series circuit with resistors R1 and R2, using a 100-volt supply. It explains that all three power formulas can be applied regardless of whether the circuit uses AC or DC. The paragraph focuses on calculating the total power consumption using the first formula, P=V*I, where the total voltage (100V) and total current (IT) are known. By using Ohm's law (V=I*R) and the series resistance (R1+R2), the total current (IT) is determined to be 2 amps. Substituting this value back into the power formula yields a power consumption of 200 watts. The paragraph also demonstrates that the other power formulas can yield the same result, albeit with additional calculations required.

Mindmap
Keywords
πŸ’‘Electrical Power
Electrical power refers to the rate at which electrical energy is transferred by an electric circuit. It is measured in watts and is a fundamental concept in the study of electricity. In the video, the calculation of electrical power is central to understanding the formulas and their applications, such as determining the power consumption of a shower or calculating the power in a simple circuit with resistors.
πŸ’‘Voltage
Voltage, measured in volts (V), is the electrical potential difference between two points. It is the force that pushes electric charge through a conductor and is a key component in the calculation of electrical power. In the context of the video, voltage is one of the variables used in the power formulas to determine the power consumption in a circuit.
πŸ’‘Current
Current, measured in amperes (amps or A), is the flow of electric charge in a circuit. It is the rate at which charge passes a particular point in a circuit and is crucial in the calculation of power. The video emphasizes the relationship between current, voltage, and power, and how to calculate current if power and voltage are known.
πŸ’‘Ohm's Law
Ohm's Law is a fundamental principle in electrical engineering that states that the current through a conductor between two points is directly proportional to the voltage across the two points and inversely proportional to the resistance between them. It is used to relate voltage, current, and resistance in a circuit, which is essential for understanding and calculating power.
πŸ’‘Resistance
Resistance, measured in ohms (Ξ©), is the opposition that a material presents to the flow of electric current. It is a property of the material and its dimensions that determine how much it resists the flow of electric charge. Resistance plays a significant role in power calculations and is a key factor in the operation of electronic components.
πŸ’‘AC and DC
AC (Alternating Current) and DC (Direct Current) are the two types of electric current. AC changes its direction periodically, while DC flows in one direction only. Understanding the difference between AC and DC is important as some power formulas are applicable to both types of current, while others are specific to one.
πŸ’‘Series Circuit
A series circuit is a type of electrical circuit where all the components, such as resistors, are connected end-to-end in a single path so that the current flows through each component in turn. The total resistance in a series circuit is the sum of the individual resistances, which affects the current and power calculations.
πŸ’‘Power Formulas
Power formulas are mathematical expressions used to calculate electrical power in a circuit. They relate voltage, current, and resistance in different ways and are essential for analyzing and designing electrical systems. The video introduces three main power formulas and explains their applications and derivations.
πŸ’‘Circuit Analysis
Circuit analysis is the process of determining the relationships between the variables in an electrical circuit, such as voltage, current, and resistance. It involves using electrical laws and formulas to calculate unknown values and understand how the circuit operates. The video demonstrates circuit analysis through the application of power formulas in a series circuit.
πŸ’‘Kilowatts
A kilowatt (kW) is a unit of power in the International System of Units (SI). It is equal to one thousand watts (W) and is commonly used to measure the power consumption of large electrical appliances or systems. In the context of the video, power is often given in kilowatts, and understanding this unit is important for practical applications.
πŸ’‘Electrical Energy
Electrical energy is the energy resulting from the movement of electric charges. It is the work done by an electric current and is related to the power and time. Electrical energy is typically measured in watt-hours (Wh) or kilowatt-hours (kWh) and is a crucial concept for understanding power consumption and billing in electrical systems.
Highlights

Introduction to the basic power formula, which is Power equals Voltage (V) times Current (I), measured in watts.

Explanation that Voltage is measured in volts, Current in amps, and Power in watts.

The usefulness of the basic power formula in practical scenarios, such as determining the current drawn by a shower.

Introduction to the second power formula derived from Ohm's law, which is Power equals Voltage (V) squared divided by Resistance (R).

Clarification that the second power formula is applicable to both AC and DC circuits.

Introduction to the third power formula, which is Power equals Current (I) squared times Resistance (R).

The third power formula is applicable to DC circuits only.

An example of a simple series circuit with resistors R1 and R2 and a 100-volt supply.

Usage of the first power formula (V times I) to calculate the power in the given series circuit example.

Explanation of how to calculate the total current (IT) in the circuit using Ohm's law.

Calculation of the total resistance (50 ohms) in the series circuit by adding R1 and R2.

Determination of the total current (IT) as 2 amps using the total resistance and voltage.

Application of the second power formula (V squared over R) to confirm the power calculation for the series circuit.

Use of the third power formula (I squared times R) to verify the power calculation, resulting in 200 watts.

Emphasis on the versatility of the power formulas and the necessity of additional calculations for their application.

The importance of understanding the domain of applicability for each power formula (DC or AC).

Transcripts

Browse More Related Video

Electrical Formulas - Basic Electricity For Beginners

Ohm's Law

Are You an Electrician? These are 5 Formulas You Should Know!

Circuits Grade 10 | Calculations

Electric power | Circuits | Physics | Khan Academy

How To Do (Almost) Any ELECTRICITY Question - GCSE & A-level Physics Exam Tip

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Electrical PowerOhm's LawPower FormulasDC CircuitsAC CircuitsVoltage CurrentResistance CalculationSeries CircuitsBasic ElectronicsEngineering Education