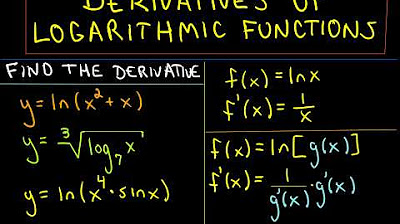Derivatives of Exponential Functions & Logarithmic Differentiation Calculus lnx, e^2x, x^x, x^sinx
TLDRThis video delves into the differentiation of exponential and logarithmic functions, focusing on rules like the power rule and logarithmic differentiation. It explains the derivative of e^(2x), the power rule for x^n, and the derivative of constants. The video also covers the derivative of a variable raised to another variable using logarithmic differentiation, providing formulas and examples for clarity. The content is enriched with detailed explanations and step-by-step solutions to complex problems like differentiating x^x and ln(x/x), making it a comprehensive guide for understanding these calculus concepts.
Takeaways
- 📚 The derivative of a function of the form e^(u), where u is a function of x, is e^u * du/dx.
- 📈 For exponential functions with a variable exponent, use the formula a^u * u' * ln(a) to find the derivative, where a is the base and u is the exponent.
- 🔢 The power rule states that the derivative of x^n is n * x^(n-1), which can be applied to any power of x, including negative and fractional exponents.
- 🌀 When differentiating a product of two functions, use the product rule: (f*g)' = f'*g + f*g'.
- 📊 To find the derivative of a natural log function, use the formula (d/dx) ln(u) = u'/u, where u is the argument of the ln function.
- 🌐 For logarithmic differentiation of a function like y = x^x, apply natural logarithms to both sides and then differentiate with respect to x.
- 🔄 When dealing with a function inside a logarithm, use the chain rule to differentiate the outer function and then apply the product rule to the inner function.
- 📶 The derivative of a constant is zero, as constants do not change with respect to the variable.
- 🧮 For more complex functions, such as y = sin(x) * ln(x), use the product rule to differentiate each part separately and then combine the results.
- 🔧 When faced with a quotient, use the quotient rule: (f/g)' = (g*f' - f*g') / g^2, and simplify the result.
- 🔄 For functions that involve both x and y, such as y = x^x, use implicit differentiation techniques to solve for dy/dx.
Q & A
What is the derivative of e to the 2x?
-The derivative of e to the 2x is 2e to the 2x. This is found using the rule that the derivative of e to the u, where u is a function of x, is e to the u times the derivative of u. Here, u is 2x and its derivative is 2.
How do you differentiate x raised to the sine x?
-To differentiate x raised to the sine x, you use logarithmic differentiation. First, set y equal to x raised to the sine x, then take the natural log of both sides to get ln y = sine x * ln x. Differentiate both sides with respect to x and you will find the derivative of x raised to the sine x.
What is the power rule for derivatives?
-The power rule states that the derivative of x raised to the n power is n times x raised to the n minus 1. For example, the derivative of x cubed is 3x squared, and the derivative of x to the four is 4x cubed.
What is the derivative of a constant?
-The derivative of any constant is zero. This is because a constant does not change with respect to the variable, so its rate of change is zero.
How do you find the derivative of e to the x squared?
-The derivative of e to the x squared is found using the rule for exponential functions. It is e to the x squared times the derivative of x squared, which is 2x. So, the derivative is 2x * e to the x squared.
What is the derivative of natural log of x squared?
-The derivative of the natural log of x squared is 2x divided by x squared (or 2/x). This is found using the rule for the derivative of ln u, which is u prime over u, where u is x squared and its derivative is 2x.
How do you differentiate a function that has a variable in the exponent, like x raised to the x?
-To differentiate a function where a variable is in the exponent, like x raised to the x, you use logarithmic differentiation. Set y equal to the function, take the natural log of both sides, then differentiate both sides with respect to x. The result will give you the derivative of the original function.
What is the derivative of e to the cosine 2x?
-The derivative of e to the cosine 2x is negative 2 sine 2x times e to the cosine 2x. This is found by first recognizing that the derivative of cosine u is negative sine u, applying the chain rule to the 2x inside the cosine, and then using the formula for the derivative of e to the u which is e to the u times u prime.
What is the derivative of 2 raised to the x?
-The derivative of 2 raised to the x is 2 raised to the x times the natural log of 2. This is found using the formula for the derivative of a to the u, which is a to the u times u prime times ln a, where a is 2, u is x, and u prime is 1.
What is the derivative of the function f(x) = x ln x?
-The derivative of the function f(x) = x ln x is ln x plus 1. This is found using the product rule, where you differentiate both x and ln x separately and then apply the rule to find the derivative of the product of these two functions.
What is the derivative of x divided by ln x?
-The derivative of x divided by ln x is 1 minus ln x divided by x squared. This is found using the quotient rule, which states that the derivative of f divided by g is g times f prime minus f times g prime divided by g squared.
Outlines
📚 Introduction to Derivatives and Exponential Functions
This paragraph introduces the topic of derivatives, specifically focusing on exponential functions such as e to the x, logarithmic functions, and logarithmic differentiation. The video aims to explain how to differentiate functions like x to the sine x and x raised to the x. It begins by discussing the derivative of e to the 2x and uses the concept of u as a function of x to derive the formula for the derivative of e raised to the u. The paragraph also reviews the power rule for differentiation, explaining how to find the derivative of x raised to the n power and how constants and variables affect the derivative.
📈 Derivatives of Exponential Functions and Logarithms
This paragraph delves into the derivatives of exponential functions such as e to the 3x, e to the 5x, and e to the x squared, and e squared. It explains the process of differentiating these functions using the formula e to the u times u prime. The paragraph also covers the derivative of a variable raised to a constant, using the formula a to the u times u prime times ln a. Additionally, it explores the derivatives of natural logs, including the derivative of ln u, and provides examples of differentiating more complex functions involving natural logs and exponents.
🌟 Derivatives of Logarithmic Functions
This paragraph focuses on the derivatives of logarithmic functions, starting with the derivative of the natural log of x. It introduces the formula for the derivative of ln u as u prime divided by u. The paragraph then applies this formula to various examples, including ln x squared, ln 2x, and ln x plus 1. It also discusses the derivatives of log base a of u, explaining the formula and providing examples of log differentiation with different bases and arguments.
🔢 Product Rule and Quotient Rule Applications
This paragraph covers the application of the product rule and quotient rule in differentiation. It explains the product rule formula and demonstrates its use in finding the derivative of functions like x ln x and x squared ln x. The paragraph also tackles the quotient rule, providing a clear explanation and applying it to differentiate functions like ln x divided by x. It emphasizes the importance of understanding these rules for more advanced differentiation problems.
🌐 Logarithmic Differentiation and Variable Exponents
This paragraph explores the concept of logarithmic differentiation for functions where a variable is raised to another variable, such as x to the x. It introduces the method of setting the function equal to y and differentiating both sides with respect to x after taking the natural log of both sides. The paragraph provides a detailed explanation and formula for this type of differentiation, along with examples to illustrate the process. It also presents an alternative formula for differentiating variables raised to other variables, which involves the product of the function and the derivative of the exponent, plus the product of the exponent and the derivative of the base, divided by the base.
Mindmap
Keywords
💡Derivatives
💡Exponential Functions
💡Logarithmic Functions
💡Chain Rule
💡Power Rule
💡Product Rule
💡Quotient Rule
💡Logarithmic Differentiation
💡Implicit Differentiation
💡Natural Logarithm
💡Exponential Growth and Decay
Highlights
Derivative of exponential functions like e^(2x) is found using the formula e^(u) * u', where u is a function of x.
The power rule states that the derivative of x^n is n * x^(n-1), which is used to find the derivative of functions like 2x^3 or 5x^5.
Derivative of a constant is zero, which applies to any constant such as e or 8 in the function.
The derivative of e^(sin(x)) is found using the chain rule, resulting in e^(sin(x)) * cos(x).
Derivative of a function like 2^(x) is found using the formula a^(u) * u' * ln(a), where u is the variable and a is the base.
The derivative of ln(u) is given by u'/u, which is applied to find the derivative of functions like ln(x^2) or ln(2x).
The derivative of ln(x) + 1 is calculated by using the quotient rule, resulting in (1 - ln(x)) / x^2.
For functions like x * ln(x), the product rule is used to find the derivative, which results in ln(x) + 1.
The derivative of x^(x) is found using logarithmic differentiation, which results in x^(x) * (ln(x) + 1).
The general formula for the derivative of a variable raised to another variable, f^g, is f^g * (g' * ln(f) + g * f' / f).
The derivative of x * sin(x) is found using the product rule, resulting in sin(x) + x * cos(x).
The derivative of x * ln(x) is calculated using logarithmic differentiation, which results in x * ln(x) + x.
The derivative of e^(u) where u is a function of x, e.g., e^(3x) or e^(x^2), is found using the formula e^(u) * u'.
Understanding the power rule and its application to functions with variable exponents is crucial for differentiation.
When differentiating functions that involve natural logs, such as ln(x) or ln(x^2), the quotient rule and properties of logs are essential.
The chain rule is applied when differentiating composite functions, such as e^(cos(2x)) or ln(sin(x)).
Logarithmic differentiation is a powerful technique for functions where a variable is raised to another variable, like y = x^x.
The process of taking the natural log of both sides of an equation and differentiating is a common method for implicit differentiation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: