Finding Derivatives Using Logarithms - Differential Calculus

The Organic Chemistry Tutor
29 Dec 201911:35
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a comprehensive guide on logarithmic differentiation, a method used to find the derivative of a function where a variable is raised to the power of another variable. It walks through the process step by step, using natural logarithms and the properties of logarithms to transform and simplify the expressions. The script provides clear examples, including the derivatives of x raised to the natural log of x, x raised to the e to the x, and sine x raised to the x, demonstrating the application of the chain rule, product rule, and power rule in differentiation. The explanation is detailed, ensuring a strong understanding of the concepts and techniques involved.

Takeaways
  • 📚 The topic is logarithmic differentiation, used to find the derivative of a variable raised to another variable.
  • 🌟 The first step is to set the expression equal to a new variable, y, to simplify the process.
  • 📈 To find the derivative of y, take the natural log of both sides of the equation before differentiating.
  • 🔄 Utilize the property of logarithms to move exponents to the front, simplifying the expression for differentiation.
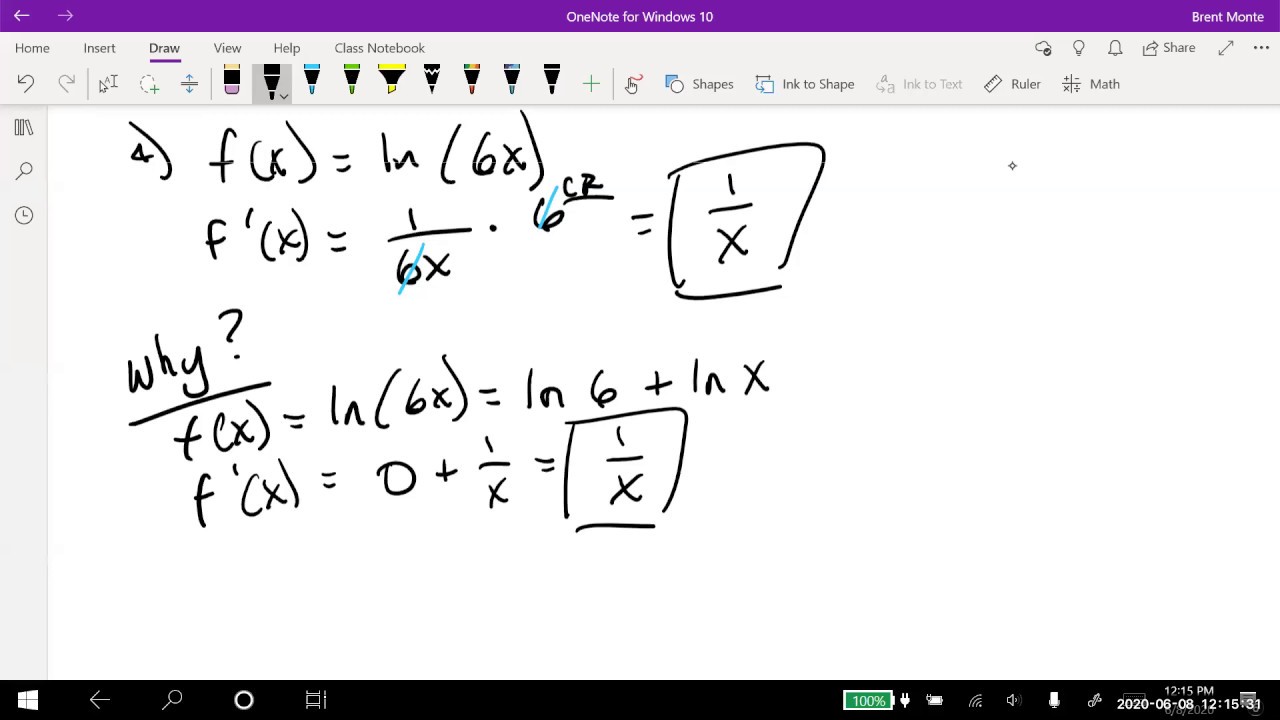
  • 👓 The derivative of a natural log expression is the derivative of the variable inside the log, divided by the variable itself.
  • 📝 When differentiating composite functions, apply the chain rule to find the derivative of the outer function and multiply by the derivative of the inner function.
  • 🌐 The derivative of ln(x^2) is 2ln(x)/x, demonstrating the power rule and chain rule in action.
  • 🔢 For the given example, the derivative of x raised to the natural log of x is 2ln(x) * x^(ln(x) - 1) after simplifying.
  • 🧠 Practice is encouraged by trying to find the derivative of other complex functions, such as x raised to e^x and sine^x.
  • 🛠 The product rule is used when differentiating a product of two functions, multiplying the derivative of each by the other function.
  • 📊 The final results of the examples show how to express the derivatives in simplified form, ready for further analysis or application.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is logarithmic differentiation, specifically how to find the derivative of a variable raised to another variable.

  • How does the video begin the process of differentiating the given expression?

    -The video begins by setting the expression equal to y and then taking the natural log of both sides of the equation to simplify the differentiation process.

  • What property of logarithms is used in the process?

    -The property used is that the natural log of a to the power of b is equal to b times the natural log of a, which allows moving the exponent to the front of the logarithm.

  • How is the derivative of y with respect to x represented?

    -The derivative of y with respect to x is represented as dy/dx or d(y)/d(x).

  • What is the derivative of the natural log expression?

    -The derivative of a natural log expression is the derivative of the variable inside the log, divided by the variable itself (e.g., d(ln x)/dx = 1/x).

  • What is the chain rule used for in this context?

    -The chain rule is used when differentiating composite functions, such as ln(x^2), to find the derivative by first taking the derivative of the outer function and then multiplying it by the derivative of the inner function.

  • How does the video simplify the final answer for the derivative of x raised to the natural log of x?

    -The video simplifies the final answer by moving the x term to the bottom of the expression and subtracting the exponents, resulting in 2 ln x * (x to the power of ln x - 1).

  • What is the process for finding the derivative of x raised to the e to the x?

    -The process involves setting the expression equal to y, taking the natural log of both sides, applying the product rule for differentiation, and factoring out common terms to simplify the result.

  • What is the role of the product rule in differentiating composite functions?

    -The product rule is used to find the derivative of a product of two functions. It states that the derivative of f times g is f prime times g plus f times g prime.

  • How does the video approach the derivative of sine x raised to the power of x?

    -The video sets the expression equal to y, takes the natural log of both sides, and then uses the product rule to differentiate, involving the natural log of sine x and x times the cotangent of x in the final result.

Outlines
00:00
📚 Introduction to Logarithmic Differentiation

This paragraph introduces the concept of logarithmic differentiation, a method used to find the derivative of a variable raised to another variable. It explains the process of setting the expression equal to y and finding its derivative (dy/dx). The video emphasizes the importance of taking the natural log of both sides of the equation before differentiating. It also highlights the special property of logarithms that allows moving the exponent to the front, exemplified by the natural log of a squared variable. The paragraph sets the stage for the detailed explanation of the differentiation process that will follow in the subsequent paragraphs.

05:01
🧠 Derivative of x Raised to the Natural Log of x

This paragraph delves into the specifics of finding the derivative of x raised to the natural log of x. It outlines the steps of taking the natural log of both sides of the equation, differentiating with respect to x, and applying the chain rule for the derivative of ln(x^2). The explanation includes the process of organizing the equation to solve for dy/dx and suggests simplifying the final answer. The paragraph also presents an alternative form of the derivative by manipulating exponents, demonstrating a clear understanding of logarithmic differentiation and its application to complex functions.

10:01
🧐 Solving Additional Examples of Logarithmic Differentiation

This paragraph continues the discussion on logarithmic differentiation by providing additional examples to reinforce the concept. It covers the derivative of x raised to the power of e^x and explains the process of taking the natural log of both sides, applying the product rule for differentiation, and factoring out common terms. Another example involves the derivative of sin(x) raised to the power of x, where the paragraph explains the use of the product rule, the derivative of the natural log of u (where u is sin(x)), and the final simplification of the expression. These examples serve to illustrate the versatility of logarithmic differentiation in solving a variety of problems.

Mindmap
Keywords
💡derivative
The derivative is a fundamental concept in calculus that represents the rate of change of a function with respect to its variable. In the context of the video, finding the derivative of an expression like x raised to the natural log of x involves using logarithmic differentiation to determine how the function changes as x varies. This is crucial for understanding the behavior of complex functions and their rates of change, as illustrated by the various examples provided throughout the video.
💡logarithmic differentiation
Logarithmic differentiation is a technique used to find the derivative of a function where one variable is expressed as a power of another variable. The process often involves taking the natural log of both sides of the equation and then differentiating with respect to x. This method is central to the video's theme, as it is the primary tool used to solve the given examples, such as finding the derivative of x raised to the natural log of x and other similar expressions.
💡natural log
The natural log, often denoted as ln, is the logarithm to the base e (approximately 2.71828). It is a key concept in the video, as it is used to transform exponential expressions into a form that can be differentiated using logarithmic differentiation. The natural log is particularly useful because of its unique properties, such as the ability to move the exponent in front of the log, which simplifies the differentiation process.
💡chain rule
The chain rule is a fundamental principle in calculus used to find the derivative of composite functions. In the video, the chain rule is applied when differentiating expressions like ln(x^2), where the outer function is the natural log and the inner function is x^2. The chain rule allows us to break down complex derivatives into manageable parts by differentiating the outer function with respect to the inner function and then multiplying by the derivative of the inner function.
💡product rule
The product rule is a calculus formula used to find the derivative of a product of two or more functions. In the video, the product rule is utilized when differentiating expressions that involve a product, such as x times ln(sin(x)). The rule states that the derivative of the product is the derivative of the first function times the second function plus the first function times the derivative of the second function. This is essential for breaking down and simplifying the differentiation process.
💡exponent
An exponent is a mathematical notation that indicates the number of times a base is multiplied by itself. In the context of the video, exponents are used to express complex functions, such as x raised to the power of the natural log of x. Understanding exponents and their properties is crucial for applying logarithmic differentiation and simplifying the resulting expressions.
💡power rule
The power rule is a basic differentiation rule that states if y = x^n, then the derivative dy/dx = n * x^(n-1). This rule is essential in the video for differentiating expressions that involve raising a variable to a power, such as in the example of ln(x^2). The power rule simplifies the process of finding derivatives by allowing us to treat the exponent as a separate factor that can be manipulated according to its own rules.
💡variable
In mathematics, a variable is a symbol that represents a number that can change. In the video, variables such as x and y are used to define functions and expressions. The process of differentiation involves finding the rate of change of these variables with respect to each other, which is crucial for understanding the behavior of functions and solving problems in calculus.
💡differentiate
To differentiate is to find the derivative of a function, which describes the rate at which the function changes. In the video, the process of differentiation is the main focus, as it is used to analyze and solve for the derivatives of various complex functions. Differentiation is a fundamental tool in calculus that helps in understanding the behavior of functions, optimization problems, and physical phenomena like motion and growth.
💡simplify
Simplification in mathematics refers to the process of making a mathematical expression or equation more straightforward or easier to understand. In the context of the video, simplification is an important step after finding the derivative of complex expressions. By simplifying the derived expressions, they become more manageable and easier to interpret, which is essential for further analysis and application in various mathematical and real-world problems.
💡examples
Examples are used in the video to illustrate the process of logarithmic differentiation and to demonstrate how to find the derivatives of functions where one variable is raised to the power of another variable. The examples, such as x raised to the natural log of x, x raised to the e to the x, and sine x raised to the x, serve to clarify the concepts and techniques discussed, providing a practical application of the theoretical concepts and helping viewers to better understand and apply the differentiation methods.
Highlights

The video discusses logarithmic differentiation, a method to find the derivative of a variable raised to another variable.

The expression x raised to the natural log of x is used as an example to demonstrate logarithmic differentiation.

The process begins by setting the expression equal to y and finding its derivative with respect to x.

Taking the natural log of both sides is a crucial step to simplify the expression for differentiation.

The special property of logarithms is used, where the natural log of a squared number can be rewritten as two times the log of the number.

The derivative of the natural log of y is 1/y times the derivative of y with respect to x.

The chain rule is applied to differentiate the expression ln x squared, which involves differentiating a composite function.

The power rule is used to deal with the exponent in the expression ln x squared.

The final derivative of x raised to the natural log of x is 2 ln x / x * x^(ln x), which is then simplified.

Another example is provided, finding the derivative of x raised to the e to the x.

The product rule is used when differentiating the product of two factors, e to the x and ln x.

The common factor e to the x is factored out to simplify the expression in the second example.

The third example involves the derivative of sine x raised to the power of x.

The natural log of both sides is taken, and the exponent is moved to the front for the third example.

The product rule is applied again for the third example, with x and ln sine x as the factors.

The derivative of the natural log of sine x is found to be cotangent x in the third example.

The final derivative for the third example is sine x raised to the power of x times the natural log of sine x plus x cotangent x.

The video effectively demonstrates the application of logarithmic differentiation for complex functions.

Transcripts

Browse More Related Video

Derivatives of Exponential Functions & Logarithmic Differentiation Calculus lnx, e^2x, x^x, x^sinx

Introduction to Logarithmic Differentiation

Calculus - Chain Rule - Derivatives

Math 11 - Section 2.3

Logarithmic Differentiation | Example: x^sinx

Indefinite Integral of 7^lnx

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsDerivativesLogarithmicDifferentiationEducationalVariable FunctionsCalculusOnline LearningMath TutorialAdvanced Math