Derivative of Logarithmic Functions

The Organic Chemistry Tutor
27 Feb 201812:12
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive guide to finding the derivatives of logarithmic functions, focusing on natural logarithms and extending to other bases. It explains the general formula for the derivative of ln u, provides step-by-step solutions to various problems, and introduces the chain rule for more complex expressions. The script covers a range of examples, from simple ln x to more intricate functions like ln(sin x) and ln(x^3), emphasizing the application of derivatives in calculus.

Takeaways
  • ๐Ÿ“š The derivative of natural log of x (ln x) is 1/x.
  • ๐Ÿ“ˆ For the derivative of ln u, use the formula (u')/u, where u is the variable inside the log function and u' is its derivative.
  • ๐ŸŒŸ When differentiating ln(u^2), the result is 2u/u or simplified to 2/x for ln(x^2).
  • ๐Ÿ”ข For ln(u^3), the derivative is (3u^2)/(u*x) which simplifies to 3/x for ln(x^3).
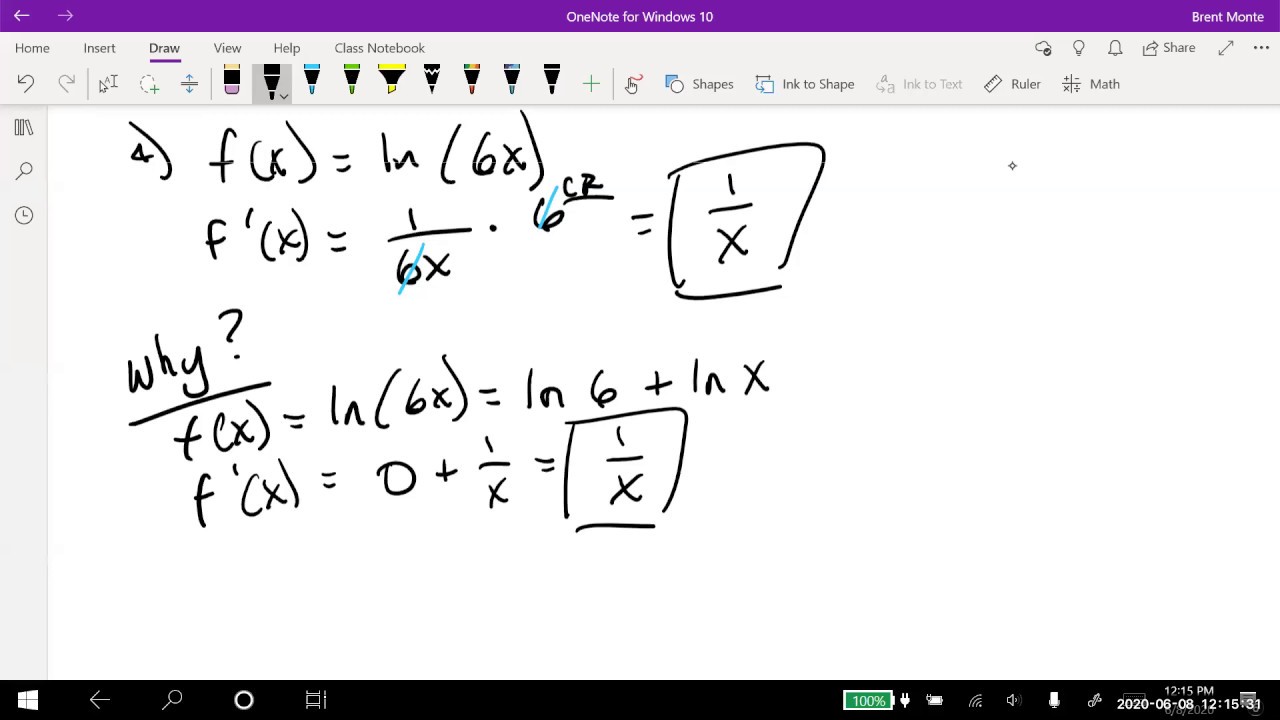
  • ๐Ÿ“Š The derivative of ln(x + c), where c is a constant, is 1/(x + c).
  • ๐ŸŒ For differentiating ln(x^2 + 4), use the formula 2x/(x^2 + 4).
  • ๐Ÿ”„ When differentiating a sum or difference inside a ln, differentiate each term individually and then combine the results.
  • ๐Ÿงฎ The derivative of ln(sin x) is cotangent x, as it represents cos(x)/sin(x).
  • ๐Ÿ› ๏ธ To differentiate ln(x^(1/7)), rewrite as x^(1/7) and apply the chain rule, resulting in (1/7)/x.
  • ๐Ÿ“ For log base a of u, the derivative is (u' * ln(a))/u, where a is the base of the logarithm.
  • ๐Ÿ”ง The derivative of log base 2 (3x - x^4) involves identifying u, u', and a, and applying the formula (u' * ln(a))/u.
Q & A

  • What is the derivative of the natural log of x (ln x)?

    -The derivative of ln x is 1/x.

  • How do you find the derivative of ln(x^2)?

    -The derivative of ln(x^2) is found by using the formula (u prime/u), where u is x^2. So, u prime is 2x, and the derivative is (2x)/x^2, which simplifies to 2/x.

  • What is the derivative of ln(x^3)?

    -For ln(x^3), the derivative is calculated as 3 times the derivative of ln x, which is 3 * (1/x), resulting in a final answer of 3/x.

  • How do you differentiate the natural log of a sum, such as ln(x + 5)?

    -The derivative of ln(x + 5) is found using the formula u prime/u, where u is x + 5. The derivative, u prime, is 1, and u is x + 5, so the derivative is 1/(x + 5).

  • What is the derivative of ln(x^2 + 4)?

    -The derivative of ln(x^2 + 4) is 2x/(x^2 + 4), using the formula u prime/u where u is x^2 + 4 and u prime is 2x.

  • How do you find the derivative of a more complex function like ln(7x + 5 - x^3)?

    -You differentiate the inner function first. The derivative of 7x is 7, the derivative of a constant (5) is 0, and the derivative of -x^3 is -3x^2. So, the derivative is 7 - 3x^2, divided by the original expression (7x + 5 - x^3).

  • What is the derivative of the natural log of the sine function, ln(sin x)?

    -The derivative of ln(sin x) is the derivative of sin x (cos x) divided by sin x, which is cotangent x (cot x).

  • How do you differentiate the natural log of the seventh root of x, ln(x^(1/7))?

    -You rewrite x^(1/7) as x to the power of 1/7, then apply the chain rule. The derivative is (1/7) * (1/x), which simplifies to 1/(7x).

  • What is the general formula for the derivative of a logarithmic function with base a, log base a of u?

    -The general formula for the derivative of log base a of u is (u prime/u) * ln(a).

  • How do you find the derivative of log base 3 of x, (log_3 x)?

    -Using the general logarithmic derivative formula, the derivative of log_3 x is (1/x) * ln(3).

  • What is the derivative of log base 4 of (x^2), (log_4 x^2)?

    -The derivative of log_4 x^2 is 2 * (x natural log of 4), as you can factor out the 2 from the log function and use the general logarithmic derivative formula.

  • How do you differentiate the natural log of the cube root of ln x, (ln^(1/3) x)?

    -You apply the chain rule and power rule. The derivative is (1/3) * ln(x)^(-2/3) * (1/x), which simplifies to (1/3x) * (ln x)^(-2/3).

Outlines
00:00
๐Ÿ“š Derivatives of Logarithmic Functions

This paragraph focuses on finding the derivatives of logarithmic functions, starting with natural logarithms. It introduces the formula for the derivative of ln(u), which is u'/u, where u is the variable. The paragraph provides examples of applying this formula to different functions, such as ln(x), ln(x^2), ln(x^3), and the natural log of sums and differences. It also explains how to simplify the expressions and the importance of understanding the derivative rules for logarithmic functions. The paragraph emphasizes the use of the chain rule for more complex derivatives, such as the cube root of ln(x), and the application of the power rule for derivatives of logarithms with different bases, like log base 3 of x and log base 4 of x^2.

05:02
๐Ÿ”ข Derivatives of Logarithmic Functions with Different Bases

This paragraph delves into the derivatives of logarithmic functions with bases other than the natural logarithm. It explains the general formula for the derivative of log base a of u, which is u'/(u*ln(a)), and applies this to examples like log base 3 of x and log base 4 of x^2. The paragraph also covers the differentiation of logarithmic functions with more complex expressions, such as log base 7 of (5 - 2x) and log base 2 of (3x - x^4). It highlights the importance of identifying the correct u, u', and a in the formula to find the derivative. Additionally, the paragraph touches on the derivative of the natural log of the natural log function, showcasing the process of differentiating nested logarithms.

10:02
๐ŸŒŸ Advanced Logarithmic Derivatives

The final paragraph discusses more advanced examples of logarithmic derivatives, including the natural log of the sine function and the natural log of the seventh root of x. It introduces the concept of trigonometric functions in the context of logarithmic derivatives, with the derivative of ln(sin(x)) being equivalent to cotangent(x). The paragraph also presents the derivative of logarithmic functions with radical expressions, such as log base 5 of tan(x), emphasizing the use of the formula u'/u*lna. The summary underscores the importance of understanding the relationship between the function, its derivative, and the base of the logarithm in order to successfully differentiate complex logarithmic expressions.

Mindmap
Keywords
๐Ÿ’กDerivative
The derivative is a fundamental concept in calculus that represents the rate of change of a function at a given point. It is used to analyze the behavior of functions, such as their slopes and critical points. In the video, the focus is on finding the derivative of logarithmic functions, which is done by applying specific rules and formulas related to derivatives.
๐Ÿ’กNatural Logarithm (ln x)
The natural logarithm, denoted as ln x, is the logarithm to the base e (where e is a mathematical constant approximately equal to 2.71828). It is a widely used function in mathematics and sciences due to its unique properties and its occurrence in natural phenomena. In the video, the derivative of ln x is derived as 1/x, which is a fundamental result used in subsequent examples.
๐Ÿ’กChain Rule
The chain rule is a crucial concept in calculus for differentiating composite functions, which are functions composed of one function inside another. It involves differentiating the outer function with respect to the inner function, then multiplying by the derivative of the inner function. In the video, the chain rule is applied when differentiating the cube root of ln x, leading to the derivative 1/(3x * (ln x)^(2/3)).
๐Ÿ’กPower Rule
The power rule is a basic differentiation rule that states if y = x^n, then the derivative dy/dx = n * x^(n-1). This rule simplifies the process of finding derivatives of power functions. In the video, the power rule is used when differentiating expressions like ln x^3, where the exponent is moved to the front as a coefficient in the derivative calculation.
๐Ÿ’กLogarithmic Functions
Logarithmic functions are mathematical functions that are the inverse of exponential functions. They are used to model a wide range of phenomena, from population growth to sound intensity. The video focuses on the derivatives of various logarithmic functions, including natural logs and logs with different bases, showing how to apply the rules of logarithms to find their derivatives.
๐Ÿ’กLog Base a of u (log_a u)
The term 'log base a of u' represents a logarithm with base 'a' of an argument 'u'. It is used to generalize the concept of logarithms beyond the natural logarithm. The derivative of such a function involves the base 'a' and is given by (u')/u * ln(a). In the video, this concept is used to differentiate logs with bases other than 'e', such as log base 3 of x or log base 4 of x squared.
๐Ÿ’กTrigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, are mathematical functions that relate the angles and sides of a triangle. They are essential in various fields, including physics and engineering. In the video, the derivative of the natural log of trigonometric functions is discussed, with the derivative of ln(sin x) being an example of how trigonometric identities are used in differentiation.
๐Ÿ’กSine Function (sin x)
The sine function is one of the six trigonometric functions, which relates the ratio of the opposite side to the hypotenuse in a right triangle to the angle in radians. The derivative of ln(sin x) is shown to be cotangent x, which is derived by applying the rules for differentiating the natural log of a function that involves a trigonometric function.
๐Ÿ’กExponential Functions
Exponential functions are mathematical functions of the form f(x) = a^x, where 'a' is a constant. They are important in modeling growth and decay processes. The video touches on exponential functions when discussing the natural logarithm, as the natural log is the inverse function of the exponential function, and this relationship is used to find derivatives.
๐Ÿ’กCritical Points
Critical points are points on the graph of a function where the derivative is zero or undefined. They are significant in calculus because they often indicate where a function has a local maximum or minimum. In the video, critical points are not explicitly discussed, but the process of finding derivatives sets the stage for identifying these points in further analysis.
๐Ÿ’กRate of Change
The rate of change is a concept in calculus that describes how quickly a quantity changes with respect to another quantity. It is the core idea behind derivatives, which provide a measure of the rate of change at any given point. The video's focus on finding derivatives of logarithmic functions is directly related to understanding and analyzing the rate of change of these functions.
Highlights

The derivative of natural log of x (ln x) is 1/x.

For the derivative of ln u, the formula is u prime divided by u.

When differentiating ln x squared, the result is 2/x by using the formula and simplifying.

For ln x cubed, the derivative is 3/x after applying the chain rule.

The derivative of ln (x + 5) is 1/(x + 5) using the u prime over u formula.

Differentiating ln (x^2 + 4) results in 2x/(x^2 + 4) by applying the derivative formula.

For aๅคๅˆ function like ln (7x + 5 - x^3), differentiate each part and combine the results.

The derivative of ln (sin x) is equivalent to cotangent x (cot x).

Differentiating the natural log of the seventh root of x yields 1/(7x) using the chain rule.

The cube root of ln x is differentiated by applying the chain rule and power rule, resulting in (1/3)ln(x)^(-2/3)/x.

The derivative of log base a of u is given by the formula u prime divided by u times ln a.

For log base 3 of x, the derivative is 1/x * ln 3.

Differentiating log base 4 of x squared gives 2 * (x * ln 4) using the formula for logarithmic derivatives.

The derivative of log base 7 of (5 - 2x) is -2/(5 - 2x) * ln 7.

For log base 2 of (3x - x^4), the derivative is a combination of derivatives of each term using the formula.

The derivative of ln(ln x) is found by differentiating both ln functions and results in 1/(x * ln x).

Transcripts

Browse More Related Video

Derivatives of Logarithmic Functions - More Examples

Derivatives of Exponential Functions

Math 11 - Section 2.3

AP Calculus AB: Lesson 3.5 Derivatives of Inverse Functions

Introduction to Logarithmic Differentiation

Integration By Parts

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Logarithmic DifferentiationMathematics TutorialCalculus ConceptsNatural LogarithmLog Base FunctionsTrigonometric FunctionsChain Rule ApplicationEducational ContentAdvanced MathDerivative Examples