Introduction to Logarithmic Differentiation

The Organic Chemistry Tutor
27 Feb 201813:31
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides a comprehensive guide on using logarithmic differentiation to find the derivatives of complex functions, such as those involving variables raised to other variables. It walks through the process step-by-step, starting with setting up the equation, taking natural logs, applying the product rule, and simplifying the expressions to arrive at the final derivatives. The script covers a variety of examples, including derivatives of x to the x, x sine x, ln x to the x, and x to the 1/x, demonstrating the versatility of logarithmic differentiation in solving advanced calculus problems.

Takeaways
  • 📚 The script explains the process of logarithmic differentiation for functions where a variable is raised to the power of another variable.
  • 🔍 To differentiate a function like y = x^x, start by setting y as x to the power of x and then take the natural logarithm of both sides of the equation.
  • 📈 The natural logarithm allows us to move the exponent to the front, resulting in ln(y) = x * ln(x), which simplifies the differentiation process.
  • 🌟 Differentiate both sides with respect to x, using the derivative of the natural logarithm (1/y * dy/dx) and applying the product rule for the right side of the equation.
  • 📊 The derivative of the function x^x is found to be dy/dx = x^x * (ln(x) + 1) after simplifying and multiplying both sides by y.
  • 🔄 For the function y = x * sin(x), follow a similar process by setting y accordingly, taking the natural log of both sides, and differentiating using the product rule.
  • 🧮 The derivative of y = x * sin(x) is dy/dx = x * cos(x) * ln(x) + sin(x) / x, after applying the product rule and simplifying the expression.
  • 📝 For the function y = ln(x)^x, take the natural log of both sides and use the product rule, with special attention to the derivative of the natural log function.
  • 🌐 The derivative of y = ln(x)^x is dy/dx = y * ln(ln(x)) + 1/ln(x), after applying the product rule and simplifying the result.
  • 🔢 For the function y = x^(1/x), take the natural log of both sides, apply the product rule, and simplify to find the derivative dy/dx = x^(1/x - 2) * (1 - ln(x)).
  • 🎓 The script emphasizes the importance of following step-by-step procedures and understanding the rules of differentiation to solve complex problems.
Q & A

  • What is the main technique used to differentiate a function where a variable is raised to the power of another variable?

    -The main technique used in this case is logarithmic differentiation.

  • How do you begin the process of differentiating a function like y = x^x?

    -You begin by setting y to x raised to the power of x, and then taking the natural logarithm of both sides of the equation.

  • What is the derivative of the natural log of y with respect to x?

    -The derivative of the natural log of y with respect to x is 1/y times dy/dx.

  • What rule is applied on the right side of the equation when differentiating y = x^x?

    -The product rule is applied on the right side of the equation when differentiating y = x^x.

  • What is the final result of differentiating y = x^x using logarithmic differentiation?

    -The final result is dy/dx = x^x * (natural log of x + 1).

  • How do you start the differentiation process for a function like y = x * sin(x)?

    -You start by setting y equal to x * sin(x), then taking the natural log of both sides, and finally differentiating both sides with respect to x.

  • What is the derivative of y = ln(x)^x?

    -The derivative of y = ln(x)^x is dy/dx = y * (1/x * ln(ln(x)) + 1/ln(x)).

  • How do you differentiate a function where the exponent is a fraction, such as y = x^(1/x)?

    -You set y equal to x^(1/x), take the natural log of both sides, and then differentiate both sides with respect to x using the product rule.

  • What is the final result of differentiating y = x^(1/x)?

    -The final result is dy/dx = x^(1/x - 2) * (1 - ln(x)).

  • What is the product rule used for differentiation, and how is it applied?

    -The product rule is used for differentiating a product of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function, plus the first function times the derivative of the second function.

  • What is the role of the natural logarithm in logarithmic differentiation?

    -The natural logarithm is used to transform an exponential function into a linear form, which makes it easier to apply differentiation rules such as the product rule.

  • Why is it necessary to multiply both sides of the differentiated equation by y when solving for dy/dx?

    -Multiplying both sides by y is necessary to isolate dy/dx on one side of the equation, which allows us to solve for the derivative of the original function.

Outlines
00:00
📚 Logarithmic Differentiation of Power Functions

This paragraph introduces the concept of logarithmic differentiation, specifically for functions where a variable is raised to the power of another variable. It explains the process of setting y equal to the function, taking the natural logarithm of both sides, and then differentiating with respect to x. The paragraph demonstrates how to use the product rule to find the derivative of such functions, providing a step-by-step solution for the function y = x^x. The final result is given as dy/dx = x^x * (ln(x) + 1). The explanation is clear and methodical, making it accessible for learners to understand and apply to similar problems.

05:02
🔄 Differentiation of Composite Functions

The second paragraph delves into the differentiation of composite functions, using the example of y = x^(sin(x)). It outlines the steps of setting y equal to the function, taking the natural logarithm of both sides, and applying the product rule to differentiate. The explanation highlights the importance of understanding the derivative of the natural logarithm function and how to manipulate the expression to simplify the final result. The paragraph concludes with the derivative dy/dx = y * (cos(x) * ln(x) + sin(x) / x), emphasizing the application of logarithmic differentiation in solving complex problems.

10:03
🌟 Advanced Logarithmic Differentiation Techniques

This paragraph presents a more advanced application of logarithmic differentiation, focusing on the function y = (ln(x))^x. It guides through the process of setting up the equation, taking the natural logarithm of both sides, and using the product rule to differentiate. The explanation is detailed, showing how to handle the derivative of the natural log function and how to simplify the expression using algebraic manipulation. The final derivative is provided as dy/dx = y * (ln(ln(x)) + 1/ln(x)), showcasing the complexity and depth of logarithmic differentiation in solving advanced mathematical problems.

Mindmap
Keywords
💡logarithmic differentiation
Logarithmic differentiation is a method used to find the derivative of a function where one variable is raised to the power of another variable. In the context of the video, it is the primary technique used to differentiate complex functions like x^x or x*sin(x). The process involves taking the natural logarithm of both sides of the equation, differentiating both sides with respect to x, and then applying rules like the product rule to simplify and find the derivative.
💡natural log
The natural log, often denoted as ln, is a logarithm to the base e (where e is an irrational number approximately equal to 2.71828). It is a fundamental concept in calculus, especially when dealing with differentiation and integration. In the video, the natural log is used to transform exponential forms into a linear form, which simplifies the process of finding derivatives.
💡derivative
A derivative is a fundamental concept in calculus that represents the rate of change or the slope of a function at a particular point. It is used to analyze the behavior of functions, including their maxima, minima, and inflection points. In the video, the derivative is calculated for various complex functions using logarithmic differentiation.
💡product rule
The product rule is a crucial rule in calculus used to find the derivative of a product of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function, plus the first function times the derivative of the second function. This rule is applied in the video when differentiating expressions that result from taking the natural log of both sides of the equation.
💡exponential function
An exponential function is a mathematical function of the form f(x) = a^x, where a is a constant and x is the variable. These functions are important in many areas of mathematics and science, as they model growth and decay processes. In the video, the concept of exponential functions is central to the differentiation problems discussed, such as differentiating x^x or x^(sin(x)).
💡variable
In mathematics, a variable is a symbol that represents a number that can change. Variables are used in formulas, equations, and functions to denote unknown quantities. In the context of the video, variables are used to create complex functions and expressions that are then differentiated using various techniques.
💡slope
The slope of a function at a particular point is a measure of how steep the graph of the function is at that point. It is synonymous with the derivative of a function at that point. In the video, the concept of slope is essential for understanding the behavior of the functions being differentiated, as the derivative provides information about the rate of change and the slope of the tangent line at any point on the curve.
💡rational function
A rational function is a function that can be expressed as the quotient or fraction of two polynomial functions. Rational functions have a wide range of applications in mathematics and are important for understanding many mathematical concepts, including limits and series. In the video, rational functions arise when differentiating certain expressions, such as 1/x, which are rewritten as x^(-1) to apply the power rule.
💡power rule
The power rule is a fundamental rule in calculus that allows for the differentiation of functions raised to a power. It states that the derivative of x^n, where n is any real number, is n*x^(n-1). This rule is used extensively in the video to differentiate expressions involving variables raised to other variables.
💡chain rule
The chain rule is a method in calculus used to differentiate composite functions, which are functions made up of other functions. It involves differentiating the outer function first and then multiplying that by the derivative of the inner function. Although not explicitly mentioned in the video, the chain rule is an essential concept for differentiating complex functions and is related to the techniques used.
Highlights

Differentiating a function where a variable is raised to the power of another variable using logarithmic differentiation.

Setting y equal to x to the power of x as the initial step in the differentiation process.

Taking the natural log of both sides of the equation to facilitate the differentiation process.

Using the product rule to find the derivative of the right-hand side of the equation after moving the exponent to the front.

The derivative of the natural log of y is 1/y times the derivative of y with respect to x.

The derivative of x is 1 times the second part, plus the first part times the derivative of the second part, which is 1/x.

Simplifying the right side of the equation to get the derivative of y with respect to x.

Multiplying both sides by y to isolate the derivative on one side.

Replacing y with the original expression to find the derivative of x raised to the power of x.

The process of differentiating x sine x by setting y equal to x sine x and taking the natural log of both sides.

Applying the product rule to differentiate sine x times ln x, using the derivatives of sine and ln x.

Multiplying both sides by y to solve for the derivative of y with respect to x in the case of x sine x.

Reverting back to the original expression to write the final derivative of x raised to the sine of x.

The process of differentiating ln x raised to the power of x by setting y equal to ln x raised to the power of x.

Using the product rule and the derivative of the natural log function to find the derivative of ln x raised to the power of x.

Simplifying the expression by canceling out x and multiplying both sides by y to isolate the derivative.

Replacing y with the original expression to obtain the final derivative of ln x raised to the power of x.

The process of differentiating x raised to the one over x by setting y equal to x raised to the one over x and taking the natural log of both sides.

Applying the product rule to differentiate 1 over x times ln x, using the derivatives of the rational function and ln x.

Simplifying the right side of the equation and multiplying both sides by y to find the derivative of y with respect to x for x raised to the one over x.

Expressing the final derivative of x raised to the one over x in terms of x raised to the power of one over x minus two times one minus ln x.

Transcripts

Browse More Related Video

Finding Derivatives Using Logarithms - Differential Calculus

Logarithmic Differentiation | Example: x^sinx

Derivative of Logarithmic Functions

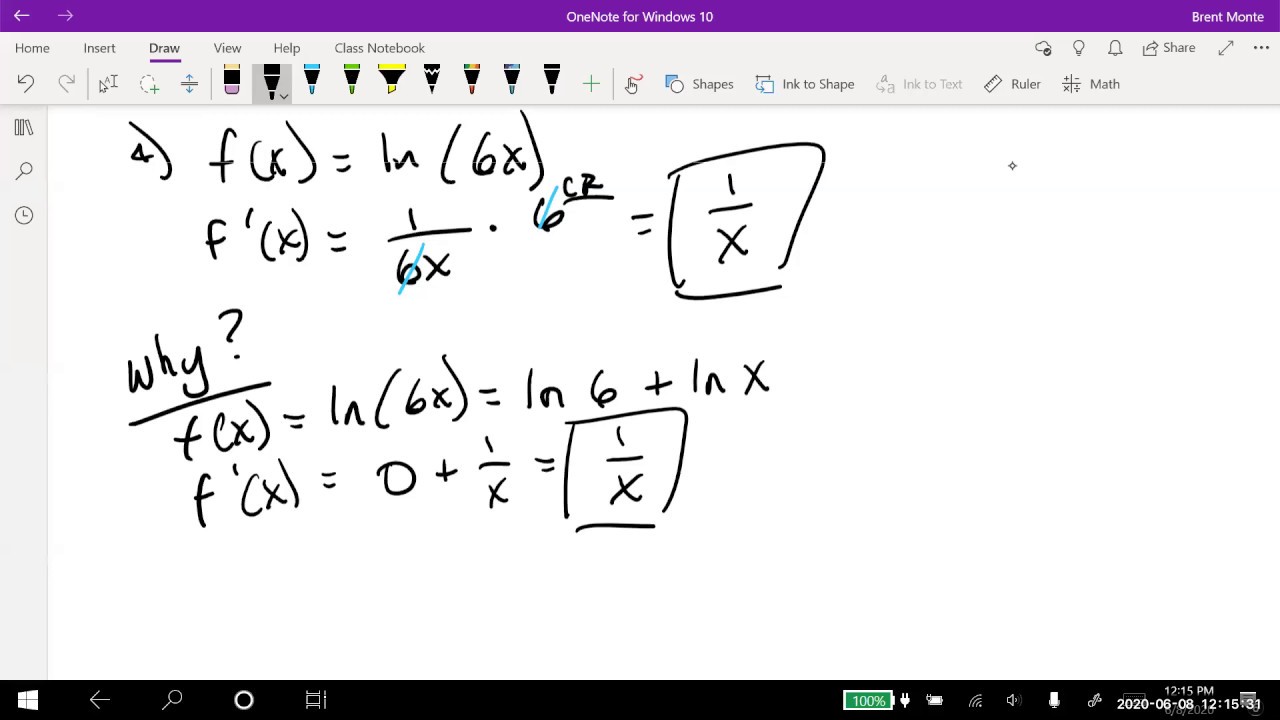
Math 11 - Section 2.3

Derivatives of Exponential Functions & Logarithmic Differentiation Calculus lnx, e^2x, x^x, x^sinx

Derivatives of Logarithmic Functions - More Examples

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Logarithmic DifferentiationCalculus TechniquesMathematical Problem SolvingAdvanced MathEducational ContentOnline LearningDifferential EquationsProduct RuleChain Rule