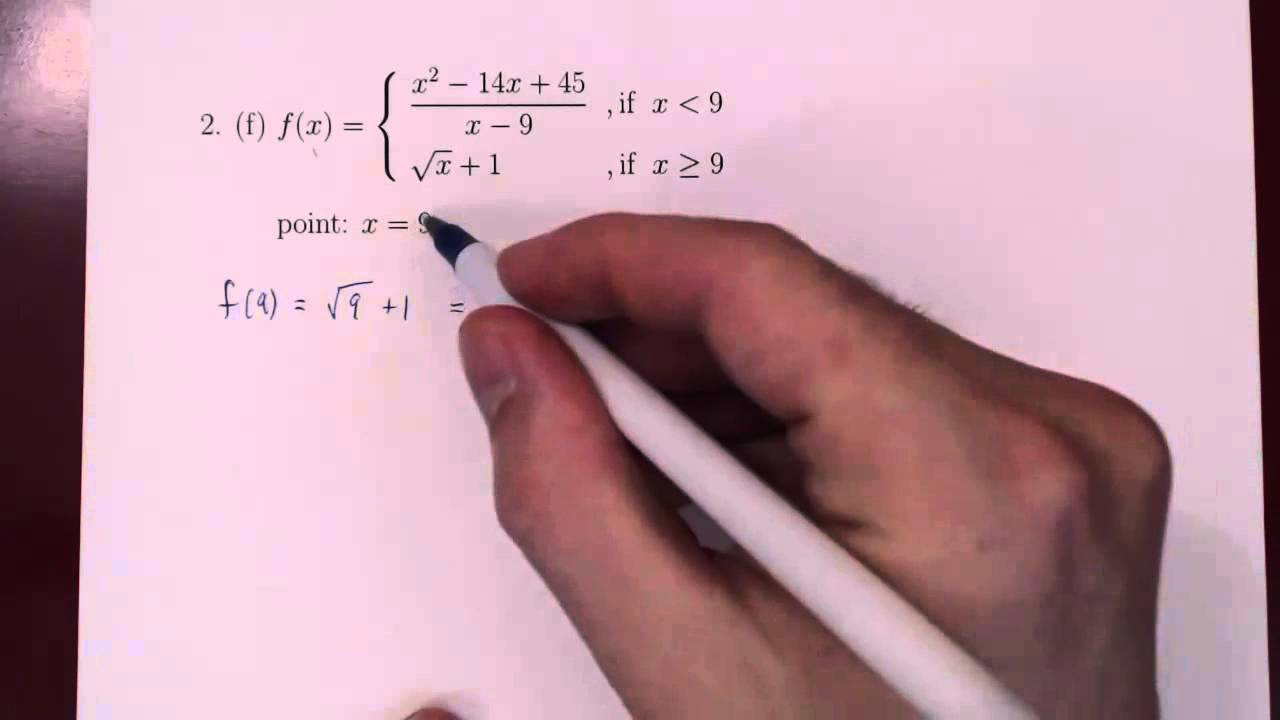GRAPH THE NIGHT M/V [Calculus Dua Lipa "Dance the Night" Parody]
TLDRThe transcript captures a student's struggle with calculus, emphasizing the concept of continuity and limits in functions. The student grapples with the idea of a function's behavior within a specific interval and the notion of limits as values approached by a function from both directions. The narrative is interspersed with moments of frustration and determination, highlighting the student's dedication to understanding derivatives, graphs, and other key calculus concepts despite the challenges and long study hours.
Takeaways
- 📚 The function is being discussed in a specific interval, not for all real numbers.
- 🔍 A function is continuous on an interval if it is contained within the function's domain and is continuous at every interior point.
- 🎵 The script mentions a song or rhythm that seems to be related to studying or the process of doing calculus.
- 🌙 The person is staying up late, possibly studying or working on calculus problems.
- 😓 The individual expresses frustration with calculus, specifically with limits and derivatives.
- 📉 The concept of a limit is emphasized, which is a fundamental part of calculus representing a value a function approaches.
- 🚫 The individual is determined not to cry or give up, showing a strong will to persevere through the challenges.
- 📌 The importance of understanding logarithms and taking the natural logarithum (Ln) is mentioned in the context of an upcoming midterm exam.
- 📈 The application of calculus in real-world scenarios, such as maximizing profits or analyzing population change, is hinted at.
- 🔧 The script touches on the use of calculus in solving problems involving rates of change, known as related rates.
- 🎓 The individual's dedication to studying is evident, as they express a willingness to graph and calculate all night to understand the material.
Q & A
What does the term 'continuous' mean in the context of a function?
-A function is considered continuous on an interval if it is defined at every point within that interval and there are no gaps or breaks in the graph of the function.
What is the significance of the domain of a function in relation to its continuity?
-The domain of a function is the set of all possible input values (x-values) for which the function is defined. A function is continuous on an interval only if that interval is contained within the function's domain.
What is an interior point of an interval?
-An interior point of an interval is any point within the interval that is not an endpoint. For a function to be continuous on an interval, it must be continuous at every interior point.
What does it mean for a function to have a limit at a certain point?
-A function has a limit at a certain point if the function values approach a specific value as the input (x) gets arbitrarily close to that point, both from the left and the right.
What is the relationship between a derivative and the rate at which a graph increases?
-The derivative of a function at a certain point represents the rate of change or the slope of the tangent line at that point on the graph. It can be used to determine how quickly the graph of the function is increasing or decreasing.
What is the main topic of the script?
-The main topic of the script is calculus, with a focus on concepts such as continuity, limits, and derivatives.
What is the significance of the phrase 'the night away' in the script?
-The phrase 'the night away' is used metaphorically to describe the speaker's dedication and struggle with studying and working on calculus problems late into the night.
What is the importance of understanding logarithms in calculus?
-Logarithms are important in calculus as they are used in solving equations, analyzing the behavior of functions, and working with exponential growth and decay. They are a key concept for solving problems in various fields of study.
How can the product rule, chain rule, and power rule help in calculus?
-These rules are essential for simplifying and differentiating more complex functions. The product rule is used for differentiating a product of two functions, the chain rule is for differentiating a composite function, and the power rule helps in differentiating functions of the form f(x) = x^n.
What is the significance of the term 'implicit differentiation' mentioned in the script?
-Implicit differentiation is a method used to find the derivative of a function that is not explicitly given in terms of the variable x. It is particularly useful when dealing with equations where the relationship between variables is not directly expressed as y = f(x).
What is the role of the limit in calculus?
-The concept of a limit is fundamental in calculus as it provides a way to understand the behavior of functions at certain points. Limits are used to define continuity, derivatives, and integrals, and they help in understanding the accumulation points and the convergence or divergence of sequences and series.
Outlines
📚 Understanding Continuous Functions
This paragraph discusses the concept of a function being continuous within a specific interval, highlighting that it must be contained within the domain of the function and that the function is continuous at every interior point of the interval. The speaker also touches on the idea of limits and derivatives, emphasizing their importance in calculus. The paragraph is interspersed with personal reflections on the challenges of studying calculus, such as staying up late, dealing with tiredness, and the pressure of upcoming exams. The speaker mentions specific topics such as logarithms, limits, derivatives, and the application of calculus in various problems, like maximizing profits and analyzing population change.
🎤 Technical Difficulties and Personal Struggles
In this paragraph, the speaker is addressing issues with their microphone and the surrounding noise, which is causing feedback and making it difficult to continue with the calculus discussion. The speaker expresses frustration and apologizes for the interruption, indicating a desire to overcome the technical difficulties. There is also a brief mention of the speaker's personal struggles, such as questioning life and dealing with dark circles under their eyes, which may be a result of the stress and effort put into studying.
Mindmap
Keywords
💡Function
💡Interval
💡Continuous
💡Limit
💡Derivative
💡Graph
💡Product Rule
💡Chain Rule
💡Implicit Differentiation
💡Logarithms
💡Radical Expressions
Highlights
The function doesn't continue after t=l 48, focusing only on the interval 0-48.
A function is continuous on an interval if it's contained within the domain and is continuous at every interior point.
The value of the function at the interval's end is the limit of the values of the function.
Limits are approached by functions from both left and right.
Every sequence is a function that eventually ends.
The concept of limits is essential for understanding the behavior of functions.
A function is continuous if it has no gaps or breaks.
Derivatives are used to determine the rate of change and the behavior of a graph.
The velocity can be shown through the graph of a function's derivative.
Logarithms and their properties are crucial for solving related calculus problems.
Midterms and exams in calculus require a deep understanding of limits and derivatives.
Product, chain, and power rules are essential for efficient problem-solving in calculus.
Implicit differentiation is a method used to differentiate expressions that do not explicitly show the variable.
The concept of limits is applied in various real-world scenarios such as maximizing profits or analyzing population change.
The natural logarithm, ln(x), is a fundamental concept in calculus.
The limit of a function as x approaches a is denoted as L'(f_x).
The importance of studying and practicing calculus to be able to graph and differentiate functions effectively.
The mention of using photo methods in MTH as an alternative to traditional study methods.
The struggle with distractions such as microphone feedback while studying.
The emphasis on the importance of a loud voice to overcome surrounding noise.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: