Displacement and distance EXAM questions: Motion in one dimension

Miss Martins Maths and Science
10 Sept 202310:45
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a detailed exploration of the concepts of distance and displacement, using various examples to illustrate the differences between the two. It begins with a cyclist traveling 400 meters east and then 700 meters west, calculating both the total distance (1100 meters) and the displacement (-300 meters to the west). The script then discusses how displacement can be calculated by choosing a positive direction and using the final and initial positions. Further examples include a runner named Aaron who runs around the perimeter of a rectangular field, calculating his total distance and displacement, and Chloe, who runs along the perimeter of a different field. The script also covers the use of Pythagoras' theorem to find the displacement when running diagonally across a rectangle. Finally, it discusses a scenario with a runner named Matthew who starts and ends at the same position, resulting in a displacement of zero. The video emphasizes the importance of understanding direction and the difference between scalar distance and vector displacement.

Takeaways
  • 📏 **Distance vs. Displacement**: Distance is the total path length traveled, regardless of direction, while displacement is the straight-line distance from the starting point to the ending point, with direction considered.
  • 🔄 **Calculating Distance**: To find the distance, sum all the individual lengths of the path traveled without considering direction.
  • ➡️ **Positive and Negative Directions**: Displacement can be calculated by choosing a positive direction and assigning the opposite direction a negative value, or vice versa.
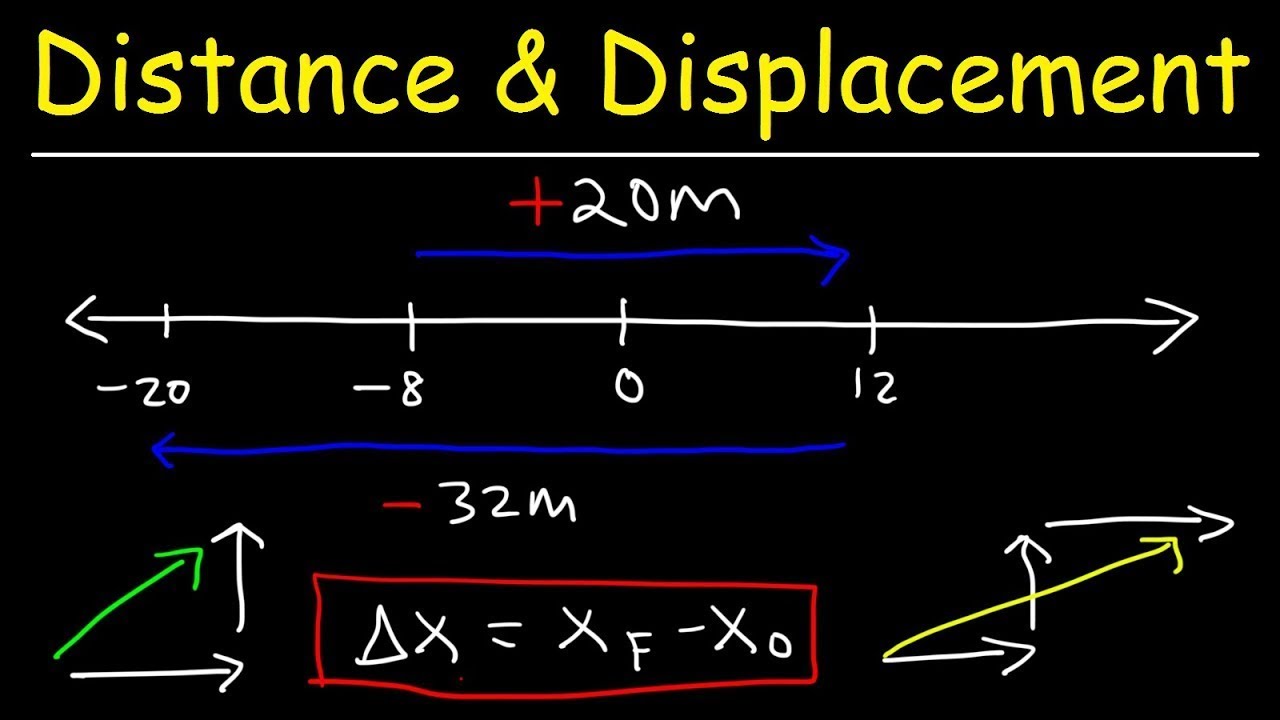
  • 🔀 **Cyclist's Example**: For the cyclist example, the total distance is the sum of 400 meters eastward and 700 meters westward, resulting in 1100 meters. The displacement is calculated as 400 meters east minus 700 meters west, resulting in -300 meters, indicating a net movement to the west.
  • 🏃 **Perimeter Running**: When running around the perimeter of a field, the total distance is the sum of all sides traversed, and displacement is the direct line from the starting to the ending point.
  • 🔵 **Rectangle Field Example**: In a rectangle, the displacement can be calculated using the Pythagorean theorem if the path forms a right-angled triangle with the sides of the rectangle.
  • 📐 **Pythagorean Theorem**: For the Chloe's run example, the displacement is found by using the Pythagorean theorem to determine the length of the diagonal from A to C.
  • 🔄 **Round Trip Displacement**: If a runner starts and ends at the same point, like Matthew in the script, the displacement is zero, even though a distance was covered.
  • 🔢 **Numerical Calculation**: Displacement involves both magnitude and direction, and can be represented as a vector from the initial to the final position.
  • 🧭 **Directional Consideration**: The direction of displacement is determined by the angle formed from the starting position to the final position, which can be described using compass directions or calculated more precisely.
  • 🔲 **Zero Displacement**: Displacement is zero when the starting and ending positions are the same, indicating no change in position despite the path taken.
  • 📚 **Further Learning**: The video script encourages viewers to check out more physics and chemistry videos for a deeper understanding of concepts like distance, displacement, and other scientific principles.
Q & A

  • What is the difference between distance and displacement?

    -Distance is the total path length traveled by an object, regardless of direction. Displacement, on the other hand, is the change in position of an object and is a vector quantity that has both magnitude and direction from the initial to the final position.

  • How do you calculate the distance traveled by the cyclist in the first example?

    -The distance is calculated by adding the lengths of the individual paths traveled. In the first example, the cyclist travels 400 meters east and then 700 meters west. The total distance is 400 meters + 700 meters = 1100 meters.

  • What is the displacement of the cyclist in the first example when considering east as the positive direction?

    -When east is considered the positive direction, the cyclist's displacement is calculated as 400 meters (eastward travel) minus 700 meters (westward travel), which equals -300 meters. The negative sign indicates the displacement is to the west.

  • How would the displacement calculation change if west is considered the positive direction instead?

    -If west is considered the positive direction, then the cyclist's displacement would be -400 meters (eastward travel, now negative) plus 700 meters (westward travel, positive), resulting in a displacement of +300 meters to the west.

  • What does the term 'perimeter' mean in the context of the second example with Aaron?

    -The term 'perimeter' refers to the outer boundary or the total length of the boundary lines of a shape. In Aaron's case, running around the perimeter means he is running along the outside edges of the field from point A to point D.

  • How is the total distance Aaron ran calculated?

    -Aaron's total distance is the sum of the lengths of each side of the rectangle he ran along. He ran 100 meters from A to B, 75 meters from B to C, and another 100 meters from C to D, making the total distance 100 + 75 + 100 = 275 meters.

  • What is the displacement of Aaron after running from point A to point D?

    -Aaron's displacement is the straight-line distance from his starting point A to his final position D, which is 75 meters directly down in the rectangle.

  • How do you calculate Chloe's displacement when she runs from point A to point C?

    -Chloe's displacement is calculated using the Pythagorean theorem because she runs along the diagonal of a rectangle. The displacement (hypotenuse) is found by taking the square root of the sum of the squares of the other two sides (250 meters and 150 meters), resulting in approximately 291.55 meters.

  • What is the total distance Matthew ran when he ran from point D to point B and back to point D?

    -Matthew's total distance is twice the length of the hypotenuse of the triangle DBC, which is calculated to be approximately 291.547559 meters. Therefore, his total distance is 291.547559 meters * 2 = 583.095118 meters.

  • What is the displacement of Matthew after running from point D to point B and back to point D?

    -Since Matthew starts and ends at the same point D, his displacement is zero meters.

  • How can one determine the direction of displacement in a more precise manner?

    -The direction of displacement can be determined more precisely by calculating the angle of the resultant vector using trigonometric functions or by using compass coordinates, which can describe the direction as a bearing (e.g., southeast).

  • What is the significance of understanding both distance and displacement in physics?

    -Understanding both distance and displacement is significant in physics as they are fundamental concepts that describe the motion of objects. Distance provides information about the total path traveled, while displacement gives information about the change in position, which is critical for analyzing the motion in terms of its start and end points.

Outlines
00:00
🚴 Understanding Distance and Displacement

This paragraph introduces the concepts of distance and displacement, emphasizing the difference between the two. It explains that distance is the total path length traveled without regard to direction, while displacement is the straight-line distance from the starting point to the final position, considering direction. The example of a cyclist traveling east and then west illustrates how to calculate both distance (1,100 meters) and displacement (-300 meters, indicating westward direction). The paragraph also clarifies the concept of choosing a positive direction for displacement and how it affects the final calculation.

05:03
🏃‍♂️ Calculating Distance and Displacement in Different Scenarios

The second paragraph delves into calculating distance and displacement in various scenarios, such as running around a field's perimeter and along the perimeter of a rectangle. It explains that distance is the sum of all traveled paths, while displacement is determined by the initial and final positions. The example of Aaron running around a rectangle's perimeter is used to calculate both his total distance (275 meters) and displacement (75 meters). The paragraph also discusses how to calculate displacement using Pythagoras' theorem in a right-angled triangle and emphasizes the need for direction in displacement calculations.

10:04
🏃‍♀️ Displacement with Zero Change in Position

The final paragraph addresses a scenario where a runner, Matthew, starts and ends at the same position, resulting in zero displacement. It calculates the total distance traveled by running from point D to B and back to D, using the hypotenuse of a triangle as the distance for the round trip. The paragraph reinforces the concept that displacement is the change in position from start to finish, which in Matthew's case is zero, despite the distance covered.

Mindmap
Keywords
💡Distance
Distance refers to the total length of the path traveled by an object, irrespective of its direction. In the video, the concept is used to calculate the total path length covered by the cyclist and Aaron as they move along their respective routes. For instance, the cyclist travels 400 meters east and then 700 meters west, resulting in a total distance of 1,100 meters.
💡Displacement
Displacement is the straight-line distance between the starting and ending points of an object's movement, with a direction indicated by its orientation from the start to the end point. The video explains that displacement is a vector quantity, calculated as the final position minus the initial position. For example, the cyclist's displacement is not the total distance traveled but rather the net movement to the west, which is 300 meters.
💡Direction
Direction indicates the orientation of movement or position relative to a chosen reference point. In the context of the video, direction is crucial for calculating displacement. The script demonstrates that choosing a positive direction (east or west) affects how displacement is calculated and interpreted. For example, if east is chosen as the positive direction, then westward movement is considered negative.
💡Perimeter
Perimeter refers to the outline or boundary line that surrounds a shape or space. In the video, Aaron runs around the perimeter of a field, which means he follows the outer edges of the field from point A to D. The perimeter is used to calculate the total distance covered by Aaron during his run.
💡Rectangle
A rectangle is a quadrilateral with four right angles, where opposite sides are equal in length. In the video, the field that Aaron runs around is a rectangle, which helps determine the distances and displacements by using the properties of rectangles and right-angled triangles within it.
💡Pythagorean Theorem
The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem is used in the video to calculate the diagonal distance (displacement) that Chloe runs from point A to C across the rectangle field.
💡Vector Quantity
A vector quantity is a physical quantity that has both magnitude and direction. Displacement is an example of a vector quantity, as it considers both how far an object has moved and in which direction. The video emphasizes that displacement is not just the straight-line distance but also includes the direction of movement.
💡Initial and Final Position
In the context of displacement, the initial position is the starting point of an object's movement, and the final position is the end point. The video explains that displacement is calculated by considering the change in position from the initial to the final position. This concept is used to determine the displacement of the cyclist and Chloe.
💡Hypotenuse
The hypotenuse is the longest side of a right-angled triangle, opposite the right angle. In the video, the hypotenuse is used to calculate the distance Matthew runs from point D to B and back to D, as well as the distance of the diagonal across the rectangle field that Chloe's displacement could theoretically follow.
💡Zero Displacement
Zero displacement occurs when an object returns to its starting position after its journey, resulting in no change in position. In the video, Matthew's run from D to B and back to D results in zero displacement because he ends at the same point where he started.
💡Compass Coordinates
Compass coordinates are directions based on the cardinal points (north, south, east, west) and their intermediates (northeast, southeast, etc.). The video mentions that one could use compass coordinates to describe the direction of Chloe's displacement from A to C, indicating the practical application of such coordinates in real-world scenarios.
Highlights

Explained the difference between distance and displacement.

Provided basic examples to calculate distance and displacement.

Distance is the total path length traveled, regardless of direction.

Displacement is calculated by choosing a positive direction and considering the change in position.

Showed how to calculate displacement with east as a positive direction.

Illustrated an alternative method of calculating displacement with west as a positive direction.

Highlighted that displacement can be negative, indicating the opposite direction of the chosen positive direction.

Discussed the concept of perimeter and its application in calculating distance.

Described how to calculate total distance run around a rectangular field.

Explained that displacement is a vector quantity pointing from the initial to the final position.

Used Pythagoras' theorem to calculate the displacement in a right-angled triangle.

Mentioned the use of compass coordinates to determine the direction of displacement.

Calculated the distance for a runner completing a round trip on a field.

Noted that if a runner starts and ends at the same position, the displacement is zero.

Emphasized the importance of interpreting negative results in displacement calculations.

Encouraged viewers to watch more physics and chemistry videos for further understanding.

Transcripts

Browse More Related Video

Displacement and Velocity - How is it different from Distance and Speed? | Physics

AP Physics Workbook 1.A Displacement

Worked example: distance and displacement from position-time graphs | AP Physics 1 | Khan Academy

Displacement vs Distance Grade 10 Science

Distance, Displacement, Average Speed, Average Velocity - Physics

Distance Versus Displacement

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Distance CalculationDisplacement AnalysisCyclist ExampleRunning ScenariosPhysics ConceptsVector QuantitiesDirection InterpretationPerimeter WalkRectangle GeometryPythagorean TheoremZero Displacement