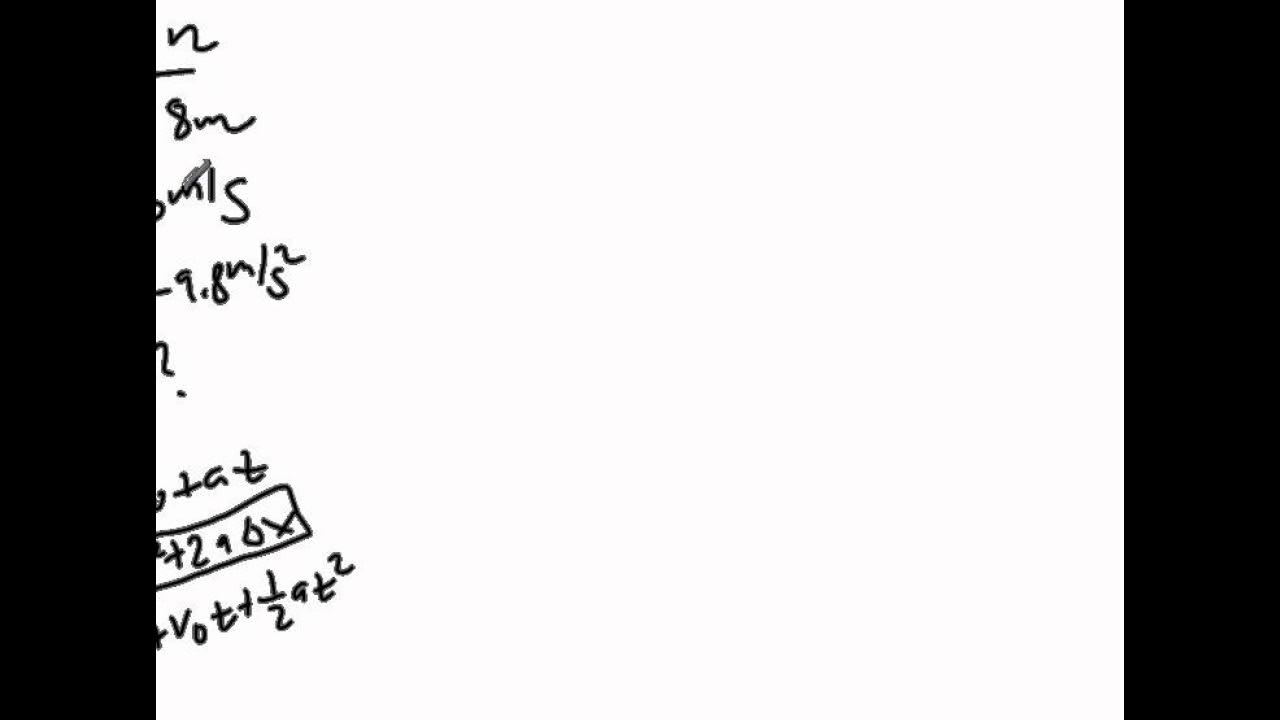Equations of Motion (Physics)
TLDRThis engaging video script explains the equations of motion through the practical example of tossing a ball, using slow-motion recording to observe the ball's upward and downward motion. The script simplifies the concept by breaking down the motion into two parts and using the three fundamental equations of motion: V = u + at, s = ut + 1/2at^2, and v^2 = u^2 + 2as. The video clarifies the difference between initial and final velocities, acceleration due to gravity, and the application of these equations to uniformly accelerated motion or uniform retardation. It also provides a hands-on approach to calculate final velocity and displacement using the given equations, with a focus on the role of gravity in freefall. The script concludes with an interactive challenge for viewers to solve test-oriented questions and contemplate the hypothetical scenario of no gravity, encouraging active participation and deeper understanding of the concepts.
Takeaways
- 📚 **Understanding Motion**: The video focuses on learning the equations of motion by observing the motion of a ball in slow motion, utilizing smartphones' slow motion recording feature.
- 🤝 **Collaboration**: It's suggested to involve a friend or family member to help record the ball's motion, as handling the ball and the recording simultaneously can be challenging.
- 📉 **Initial and Final Velocities**: The video explains the concepts of initial velocity (starting speed) and final velocity (ending speed), emphasizing that the ball starts from rest and gains speed due to gravity.
- 🔢 **Equations of Motion**: Three key equations of motion are introduced: V = u + at, s = ut + 0.5*at^2, and v^2 = u^2 + 2as, where V is final velocity, u is initial velocity, a is acceleration, t is time, and s is displacement.
- 🧲 **Acceleration Due to Gravity**: The video clarifies that the acceleration due to gravity is approximately 10 m/s^2 and is the same for all objects in free fall, regardless of their mass.
- ⏱️ **Time Measurement**: The time taken for the ball's motion can be measured with a stopwatch, which is an essential parameter in the equations of motion.
- 📈 **Uniform Acceleration and Retardation**: The equations are applicable to uniformly accelerated motion or uniform retardation, meaning the speed increases or decreases at a constant rate.
- 🚀 **Upward and Downward Motion**: The video distinguishes between the upward motion (with initial velocity greater than zero and final velocity zero) and downward motion (with initial velocity zero and final velocity non-zero), with different signs of acceleration for each.
- 📐 **Displacement**: Displacement is the distance covered by the ball during its motion and is a key variable in the equations, often confused with speed but distinct in terms of scalar versus vector quantities.
- 🔁 **Retardation in Upward Motion**: During upward motion, the ball experiences negative acceleration (retardation), which is represented as -10 m/s^2 in the equations.
- 🌌 **No Gravity Scenario**: The video humorously explores the hypothetical scenario of no gravity, suggesting that a ball would continue in a straight line indefinitely, illustrating Newton's first law of motion.
Q & A
What is the initial speed of the ball when it is dropped?
-The initial speed of the ball when it is dropped is zero, as it starts from rest.
What is the term used to describe the speed of the ball at the end of its motion?
-The speed of the ball at the end of its motion is referred to as the final speed or final velocity.
What are the three equations of motion discussed in the script?
-The three equations of motion discussed are: V = u + at, s = ut + (1/2)at^2, and v^2 = u^2 + 2as.
What does the symbol 'a' represent in the equations of motion?
-In the equations of motion, 'a' represents the acceleration of the ball, which is the rate of increase of velocity.
What is the typical acceleration due to gravity on Earth?
-The typical acceleration due to gravity on Earth is 10 meters per second squared.
What is the initial velocity of the ball during its upward motion?
-The initial velocity of the ball during its upward motion is greater than zero because a force is applied to it, giving it speed.
What is the final velocity of the ball at the peak of its upward motion?
-The final velocity of the ball at the peak of its upward motion is zero, as it momentarily stops before falling back down.
What is the acceleration of the ball during its upward motion?
-The acceleration of the ball during its upward motion is negative, specifically -10 meters per second squared, indicating a deceleration or retardation.
What is the displacement of the ball after one second of free fall?
-The displacement of the ball after one second of free fall is 5 meters, calculated using the equation s = ut + (1/2)at^2 with u = 0, a = 10 m/s^2, and t = 1 second.
How can you calculate the initial velocity when a ball is thrown upwards?
-You can calculate the initial velocity using the first equation of motion, V = u + at, where V is the final velocity (which is zero at the peak), a is the acceleration due to gravity (-10 m/s^2 for upward motion), and t is the time taken to reach the peak.
What happens to the ball's velocity as it travels upwards?
-The ball's velocity decreases as it travels upwards due to the negative acceleration (retardation) acting on it, which is caused by gravity.
What is the difference between displacement and distance in the context of the script?
-In the context of the script, displacement refers to the straight-line distance between the initial and final positions of the ball, taking into account the direction of motion. Distance, while often used interchangeably with displacement in the script, technically refers to the total path length traveled by the ball, without regard to direction.
Outlines
🏐 Understanding Motion Through Ball Toss Experiment
This paragraph introduces the concept of motion through a practical experiment of tossing a ball and observing its motion in slow motion using a smartphone's recording feature. The video aims to simplify the equations of motion and demonstrates the difference between upward and downward motion. The initial and final velocities of the ball are discussed, with the initial velocity being zero at the start of the downward motion and the final velocity being non-zero as the ball gains speed. The equations of motion are introduced: V = u + at, s = ut + 1/2at^2, and v^2 = u^2 + 2as, where V is the final velocity, u is the initial velocity, a is the acceleration, t is the time, and s is the displacement. The importance of understanding the difference between speed and velocity, as well as distance and displacement, is highlighted.
📐 Applying Equations of Motion to Uniform Acceleration and Retardation
The second paragraph delves into the application of the equations of motion, clarifying that they are applicable to uniformly accelerated motion or uniform retardation. It explains that uniform acceleration means the object's speed increases at a constant rate, while uniform retardation means the object's speed decreases at a constant rate. The video provides examples and shows how to calculate the final velocity and displacement of a ball after one second using the equations of motion, taking into account the acceleration due to gravity. The paragraph emphasizes that during free fall, all objects accelerate at the same rate, regardless of their mass.
⏫ Analyzing Upward and Downward Motion with the Equations of Motion
This paragraph focuses on the analysis of upward motion by throwing the ball upwards. It discusses the initial and final velocities during the upward motion, noting that the initial velocity is greater than zero due to the applied force, while the final velocity at the top is zero as the ball momentarily stops. The concept of retardation or negative acceleration is introduced, with the acceleration value for upward motion being -10 m/s^2. The video demonstrates how to calculate the initial velocity given a time of one second to reach the maximum height and how to find the final velocity after the ball has traveled a certain distance. The differences between downward and upward motion in terms of initial and final velocities and acceleration are summarized.
🤔 Interactive Learning and Hypothetical Scenario Without Gravity
The final paragraph encourages an interactive approach to learning by inviting viewers to answer test-oriented questions in the comments section and to ask doubts or provide feedback. It poses a hypothetical scenario where the ball is thrown in a no-gravity environment, illustrating the concept of motion without the influence of Earth's gravity. The video concludes with a call to action for viewers to like, comment, share, and subscribe to the channel.
Mindmap
Keywords
💡Equations of Motion
💡Slow Motion
💡Initial Velocity
💡Final Velocity
💡Acceleration
💡Displacement
💡Uniform Acceleration
💡Free Fall
💡Retardation
💡Scalar and Vector Quantities
💡Test-Oriented Questions
Highlights
The video demonstrates the equations of motion by tossing a ball and observing its motion in slow motion.
Smartphones with slow motion recording capabilities can be used to capture and analyze the motion of the ball.
The motion of the ball is split into upward and downward parts for separate analysis.
The initial velocity of the ball at the start of its downward motion is zero.
The final velocity of the ball at the bottom is greater than zero, indicating acceleration due to gravity.
The three fundamental equations of motion are introduced: V = u + at, s = ut + 1/2at^2, and v^2 = u^2 + 2as.
The symbols in the equations represent initial velocity (u), final velocity (v), time (t), acceleration (a), and displacement (s).
An important exam tip is that speed and velocity, as well as distance and displacement, are often used interchangeably in problems.
The equations of motion are applicable to uniformly accelerated motion or uniform retardation.
For constant speed or velocity, simple equations such as distance = speed × time can be used instead.
The acceleration due to gravity is approximately 10 meters per second squared during freefall.
The final velocity of the ball after one second of freefall can be calculated using the first equation of motion.
The displacement of the ball after one second is five meters, calculated using the second equation of motion.
For upward motion, the initial velocity is greater than zero, and the final velocity at the top is zero, indicating retardation.
The value of acceleration for upward motion is minus ten meters per second squared, indicating deceleration.
The initial velocity for an upward thrown ball can be calculated using the first equation of motion with the final velocity as zero.
The final velocity of a ball thrown upwards with an initial velocity of 5 m/s after traveling a distance of 1 meter is approximately 2.24 m/s.
A comparison between downward and upward motion is summarized, highlighting differences in initial and final velocities, acceleration, and displacement.
The video concludes with interactive questions for the audience to solve, encouraging engagement and application of the concepts learned.
A thought experiment is presented, speculating on what would happen if a ball were thrown in a no-gravity environment.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: