Calculating Residuals and MSE for Regression by hand

Katie Ann Jager
13 Nov 201605:17
EducationalLearning
32 Likes 10 Comments

TLDRThis video script demonstrates the process of calculating residuals and estimating Sigma squared for a least squares regression line. It uses a simple dataset and the equation Y hat = 1.5 + 1.5x to predict values and determine the differences between observed and predicted Y values. The script then explains how to compute the mean squared error (MSE), also known as Sigma squared, by summing the squares of the residuals and dividing by the appropriate denominator. The example illustrates the foundational concepts of regression analysis in an accessible manner.

Takeaways
  • 📊 The script explains the process of calculating residuals and estimating Sigma squared in the context of least squares regression.
  • 🔢 Residuals are the differences between the observed values (Y) and the predicted values (Y-hat) for the same X value.
  • 📈 The least squares regression line is given as Y-hat = 1.5 + 1.5X, which is used to predict Y values based on X values.
  • 🧮 For the first observation (X=1), the predicted value (Y-hat) is calculated as 3, using the given regression line.
  • 📊 For the second observation (X=2), the predicted value (Y-hat) is 4.5, following the same calculation method.
  • 📈 The predicted value for the last observation (X=3) is 6, as derived from the regression equation.
  • 🤔 Residuals for each observation are calculated by subtracting the predicted values from the actual observed values.
  • 📊 The script provides an example calculation of residuals: 0 for the first, 0.5 for the second, and 0 for the third observation.
  • 🧠 Estimating Sigma squared (Σ²) involves summing the squared residuals and dividing by (n - k + 1), where n is the number of observations and k is the number of explanatory variables.
  • 🔢 In this case, Sigma squared is estimated to be 0.25, calculated by squaring the residuals and dividing by 2 (since n=4 and k=1).
  • 📝 The estimated Sigma squared represents the mean squared error (MSE) and is an indicator of the true variation in the population or sample data.
  • 💡 The process demonstrated in the script can be automated using software, especially for larger datasets.
Q & A

  • What is the main purpose of calculating residuals in a least squares regression analysis?

    -The main purpose of calculating residuals is to determine the difference between the observed values (Y) and the predicted values (Y-hat) for the same value of X. This helps in assessing the accuracy and fit of the regression model to the data.

  • Given the least squares regression line Y-hat = 1.5 + 1.5X, how do you calculate the predicted value for the first observation when X is equal to 1?

    -For the first observation where X is equal to 1, you substitute the value of X into the regression equation. So, Y-hat = 1.5 + 1.5(1), which simplifies to Y-hat = 3.

  • What is the predicted value of Y when X is 2 in the given example?

    -When X is 2, the predicted value of Y (Y-hat) is calculated as 1.5 + 1.5(2), which equals 4.5.

  • How do you calculate the residual for the second observation in the data set?

    -The residual for the second observation is calculated by subtracting the predicted value (Y-hat) from the actual observed value (Y). If Y is 4.5 for the observed value when X is 2, then the residual is 4.5 - 4.5, which equals 0.

  • What is the formula for calculating the estimate of Sigma squared (Σ²) in the context of least squares regression?

    -The estimate of Sigma squared (Σ²), also known as the mean squared error (MSE), is calculated using the formula Σ(Y - Y-hat)² / (N - k), where N is the number of observations, k is the number of parameters in the model (including the intercept), and the sum is taken over all observations.

  • In the provided script, what is the value of k in the calculation of Sigma squared?

    -In the provided script, k is equal to 1 because there is only one explanatory variable (X) in the model.

  • How many residuals were calculated in the example provided in the script?

    -Three residuals were calculated in the example, one for each observation in the data set.

  • What does the value of the estimated Sigma squared indicate in a regression analysis?

    -The estimated Sigma squared represents the average squared deviation of the residuals from the predicted values. It is an estimate of the true variation in the population or sample, providing a measure of the model's accuracy and the degree of dispersion around the regression line.

  • What is the estimated Sigma squared for the small data set in the script?

    -The estimated Sigma squared for the small data set in the script is 0.25.

  • How can software be utilized in calculating residuals and Sigma squared for larger data sets?

    -Software can automate the calculations of residuals and Sigma squared, making the process more efficient and less prone to human error. It can handle large amounts of data and perform the necessary computations quickly and accurately.

  • What is the significance of calculating residuals and Sigma squared in the context of model validation?

    -Calculating residuals and Sigma squared is crucial for model validation as it allows us to assess the model's performance and fit to the data. It helps in identifying patterns in the residuals that might indicate issues with the model, such as non-linearity or the presence of outliers, and provides a quantitative measure of the model's predictive accuracy.

Outlines
00:00
📊 Calculating Residuals and Estimating Sigma Squared

This paragraph explains the process of calculating residuals and estimating Sigma squared (σ^2) using the least squares regression line, Y hat = 1.5 + 1.5x, for a given small data set. It details the steps to find the predicted values (Y hat) for different X values, and then how to compute the residuals (Y - Y hat) as the difference between observed and predicted Y values. The calculation involves plugging in X values into the regression equation and finding the discrepancies for each observation. The paragraph also describes how to estimate the mean squared error (MSE), which is equivalent to σ^2, by summing the squared residuals and dividing by (n - k + 1), where n is the number of data points and k is the number of explanatory variables. The example uses a data set with 4 observations and 1 explanatory variable (X), leading to a denominator of (4 - 1 + 1) for the MSE calculation. The result is an estimated σ^2 value of 0.25, representing the true variation in the population or sample.

05:02
📱 Using Software for Large Data Sets

The second paragraph briefly discusses the practicality of using software for calculating residuals and estimating Sigma squared for larger data sets. It suggests that while the manual calculation demonstrated in the previous paragraph is feasible for small data sets, it is more efficient and likely to be employed when dealing with a larger volume of data. The paragraph implies that software can automate the process, reducing the potential for human error and saving time, without going into specifics about the software or the automation process.

Mindmap
Keywords
💡residuals
Residuals refer to the differences between the observed values and the predicted values in a regression analysis. In the context of the video, they are calculated by subtracting the predicted y-values (y-hat) from the actual observed y-values for each data point. This helps in assessing the accuracy of the regression model and identifying any patterns in the data that the model may not be capturing.
💡least squares regression line
The least squares regression line, also known as the line of best fit, is a直线 that best represents the data in a scatter plot. It is calculated by minimizing the sum of the squares of the residuals. In the video, the given regression line is Y-hat = 1.5 + 1.5x, which indicates that for every one-unit increase in x, the predicted y-value increases by 1.5 units.
💡Sigma squared (Σ²)
Sigma squared (Σ²) is an estimate of the variance, which measures the spread of the residuals around the regression line. It is calculated as the mean of the squared residuals and provides insight into the overall variability or dispersion of the data points in relation to the model's predictions.
💡predicted value (y-hat)
The predicted value, often denoted as y-hat (ŷ), is the value of the dependent variable that a regression model estimates for a given set of independent variable(s). It is calculated using the coefficients from the regression equation and the values of the independent variables.
💡observed value (y)
The observed value (y) is the actual data point or measurement that is collected for the dependent variable in an experiment or dataset. It is used in comparison to the predicted value (y-hat) to assess the accuracy and fit of a statistical model.
💡mean squared error (MSE)
Mean Squared Error (MSE) is a measure of the average squared difference between the predicted values and the actual observed values. It is used to quantify the performance of a regression model, with a lower MSE indicating a better fit to the data.
💡regression analysis
Regression analysis is a statistical method used to examine the relationship between one or more independent variables and a dependent variable. It helps in identifying trends, predicting outcomes, and determining the strength and direction of the relationships between variables.
💡coefficients
Coefficients are the numerical values in a regression equation that represent the relationship between the independent and dependent variables. They quantify the change in the dependent variable for each unit change in the independent variable.
💡variance
Variance is a statistical measure that quantifies the spread or dispersion of a set of data points. It is calculated as the average of the squared differences from the mean and provides an understanding of how data points are distributed relative to the mean.
💡data points
Data points are individual values or observations within a dataset that represent the intersection of specific values of variables. In the context of a scatter plot, each data point is represented as a coordinate on a graph, with one value on the x-axis and another on the y-axis.
💡model accuracy
Model accuracy refers to how well a statistical model represents the data it is intended to describe. It is often assessed using various metrics such as residuals, mean squared error, and other goodness-of-fit measures.
Highlights

Calculation of residuals using the least squares regression line formula Y hat = 1.5 + 1.5x

Explanation of residuals as the difference between observed and predicted values for the same x value

Step-by-step calculation of predicted y-values for given x-values in the data set

Use of the first observation (X=1) to demonstrate the calculation of the predicted value (Y hat = 3)

Application of the regression line formula to find the predicted value for X=2 (Y hat = 4.5)

Computation of the predicted value for the last observation with X=3 (Y hat = 6)

Derivation of residuals for each data point by subtracting the predicted values from the observed values

Example calculation of residuals showing 0.5 and 0 for the first two observations

Description of the process to calculate the estimate for Sigma squared (MSE) using residuals

Explanation of the formula for Sigma squared calculation as the sum of squared residuals divided by (N - K + 1)

Use of the given data set to calculate the value of Sigma squared (0.25) using the residuals and the formula

Clarification that Sigma squared represents the true variation in the population or the mean squared error in a sample

Suggestion that the calculations can be performed using software for larger data sets

Demonstration of the entire process from calculating predicted values to estimating Sigma squared for a small data set

The importance of understanding the relationship between observed and predicted values in regression analysis

The role of residuals in assessing the fit of the regression model to the data

The significance of Sigma squared in determining the variability and accuracy of the regression model

Transcripts

Browse More Related Video

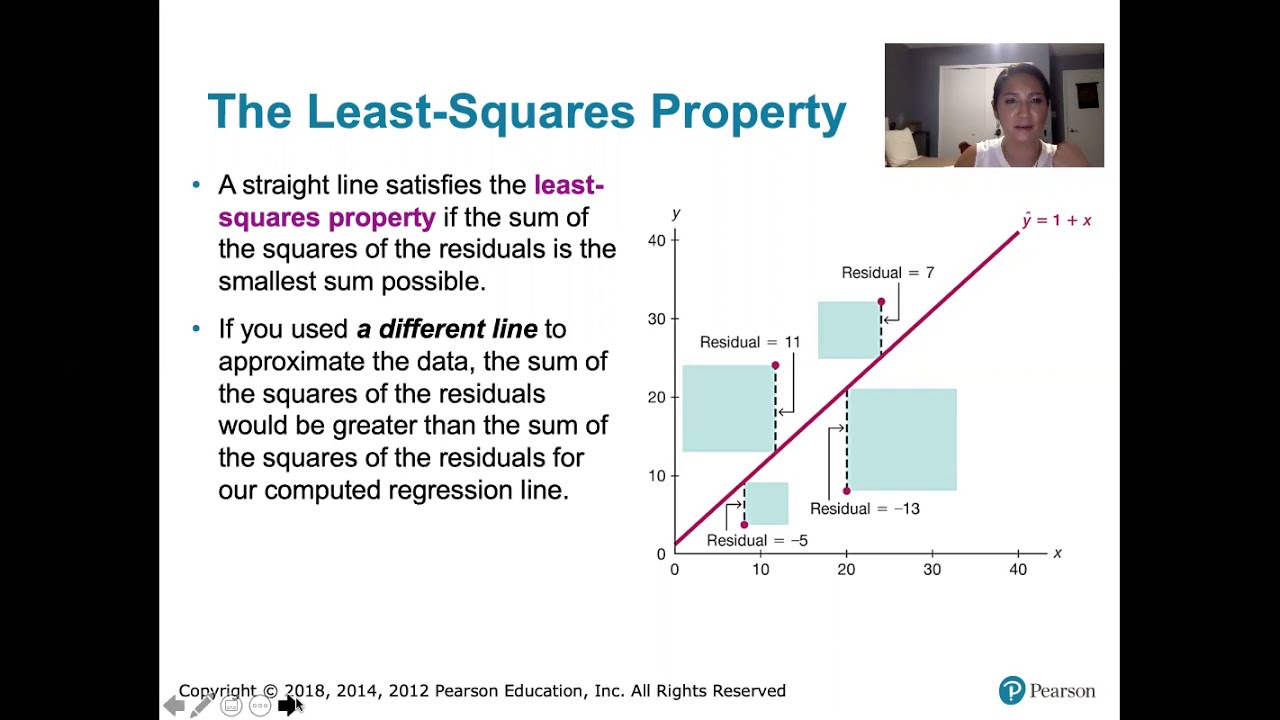
10.2.5 Regression - Residuals and the Least-Squares Property

Residuals and Residual Plots

Introduction to residuals and least squares regression

The Main Ideas of Fitting a Line to Data (The Main Ideas of Least Squares and Linear Regression.)

How to Calculate the Residual

Introduction to REGRESSION! | SSE, SSR, SST | R-squared | Errors (ε vs. e)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Regression AnalysisStatistical LearningData InterpretationPredictive ModelingMath TutorialLeast Squares MethodResidual CalculationSigma EstimationError Analysis