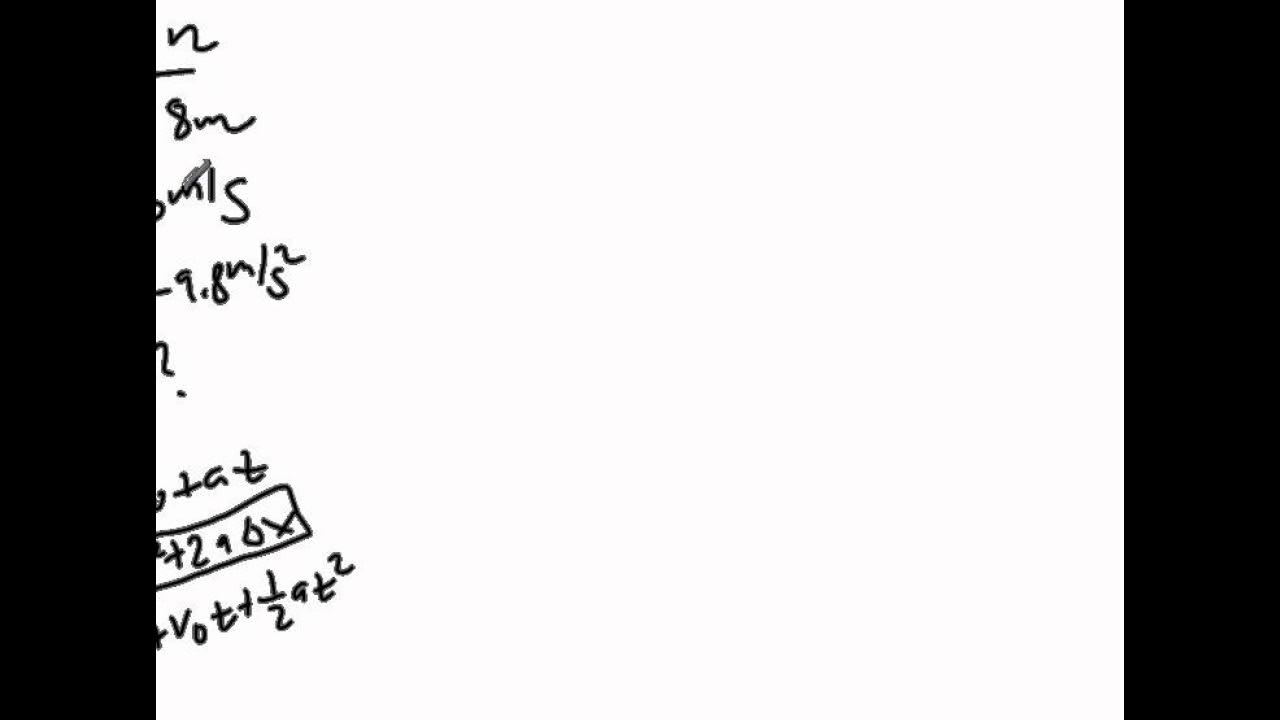AP Physics B Kinematics Presentation #31

The New Jersey Center for Teaching and Learning
26 Jun 201203:19
EducationalLearning
32 Likes 10 Comments

TLDRThe video script demonstrates how to calculate acceleration using the kinematic equation \( v^2 = v_0^2 + 2a\Delta x \). Starting with initial and final velocities of 20 m/s and 60 m/s, respectively, and a distance traveled of 200 meters, the script guides through the steps of isolating acceleration 'a'. By substituting the given values, the script concludes with an acceleration of 8 meters per second squared, showcasing a clear and methodical approach to solving physics problems.

Takeaways
  • 🚀 The problem involves calculating acceleration over a given distance with known initial and final velocities.
  • ⏱ The initial velocity given is 20 meters per second, and the final velocity is 60 meters per second.
  • 📏 The distance traveled during the acceleration is 200 meters.
  • 🔍 Three kinematic equations are presented: v = v₀ + at, v² = v₀² + 2ad, and x = x₀ + v₀t + 1/2at².
  • 📘 The chosen equation for solving the problem is v² = v₀² + 2ad, as it relates initial and final velocities and displacement.
  • 📝 The process involves isolating 'a' (acceleration) by manipulating the equation to a = (v² - v₀²) / (2d).
  • 🔢 The calculation steps include subtracting v₀² from both sides and then dividing by 2d.
  • 📉 Squaring the final and initial velocities gives 3600 m/s² and 400 m/s² respectively.
  • 📈 The acceleration is found by dividing the difference of these squared velocities (3200 m²/s²) by twice the distance (400 m).
  • 🔑 The result of the division simplifies to 32/4, which equals 8 m/s², representing the acceleration.
  • 📚 The units of acceleration are correctly identified as meters per second squared.
Q & A

  • What is the initial velocity mentioned in the script?

    -The initial velocity mentioned in the script is 20 meters per second.

  • What is the final velocity in the given scenario?

    -The final velocity is 60 meters per second.

  • What is the total distance traveled in the problem described?

    -The total distance traveled is 200 meters.

  • Which kinematic equation is chosen to solve for acceleration in the script?

    -The kinematic equation chosen to solve for acceleration is \( v^2 = v_0^2 + 2a\Delta x \).

  • What is the first step in solving for acceleration according to the script?

    -The first step is to subtract \( v_0^2 \) from both sides of the equation to isolate the term with acceleration.

  • What is the result of the equation after subtracting \( v_0^2 \) from both sides?

    -The result is \( 2a\Delta x = v^2 - v_0^2 \).

  • How is the acceleration 'a' isolated in the equation?

    -The acceleration 'a' is isolated by dividing both sides of the equation by \( 2\Delta x \).

  • What is the formula for acceleration after isolating 'a'?

    -The formula for acceleration is \( a = \frac{v^2 - v_0^2}{2\Delta x} \).

  • What are the values substituted into the formula for the final and initial velocities?

    -The values substituted are 60 m/s for the final velocity and 20 m/s for the initial velocity.

  • What is the calculated acceleration in meters per second squared?

    -The calculated acceleration is 8 meters per second squared.

  • How does the script ensure the units are correct for acceleration?

    -The script ensures the units are correct by showing the cancellation of meters squared in the numerator and denominator, leaving meters per second squared.

Outlines
00:00
🚀 Calculating Acceleration Using Kinematic Equations

This paragraph explains the process of calculating acceleration given initial and final velocities and the distance traveled. The initial velocity is 20 m/s, the final velocity is 60 m/s, and the distance covered is 200 meters. The speaker chooses the kinematic equation \( v^2 = v_0^2 + 2a\Delta x \) to solve for acceleration 'a'. By rearranging the equation to isolate 'a', the formula becomes \( a = \frac{v^2 - v_0^2}{2\Delta x} \). Plugging in the given values, the calculation yields an acceleration of 8 m/s², which is the final result after simplifying the expression.

Mindmap
Keywords
💡initial velocity
Initial velocity is the speed at which an object starts moving. In the context of the video, the initial velocity is given as 20 meters per second. This term is crucial for calculating acceleration, as it represents the starting point of the object's motion before any acceleration occurs.
💡final velocity
Final velocity is the speed at which an object is moving at the end of a period of acceleration. In the video, the final velocity is 60 meters per second. This term helps determine the change in speed and is essential for calculating acceleration.
💡distance
Distance refers to the total length of the path traveled by the object. In the video, the object travels a distance of 200 meters. This value is used in the kinematic equation to find the acceleration.
💡acceleration
Acceleration is the rate of change of velocity of an object. It is the primary variable being solved for in the video, calculated using the kinematic equation and given values. The video's problem-solving approach revolves around determining this value.
💡kinematic equations
Kinematic equations are formulas used to describe the motion of objects under constant acceleration. The video mentions three specific equations and chooses the one most appropriate for the given problem. These equations relate variables such as velocity, acceleration, and distance.
💡v squared equals v naught squared plus 2a delta x
This kinematic equation relates the final velocity, initial velocity, acceleration, and distance. It is selected in the video to solve for acceleration because the initial velocity, final velocity, and distance are known. This equation simplifies the process of finding acceleration.
💡solve for a
Solving for 'a' means isolating the acceleration variable in the equation. In the video, the steps to rearrange the chosen kinematic equation to solve for acceleration are shown in detail. This process includes algebraic manipulation to isolate and calculate the value of acceleration.
💡v squared minus v naught squared
This expression represents the change in the square of velocities. In the video, it's calculated as part of solving the kinematic equation for acceleration. The difference between the squares of the final and initial velocities is key to finding the acceleration.
💡200 meters
This is the given distance traveled by the object. It is a critical value in the calculation of acceleration, used in the denominator when applying the kinematic equation. The distance helps determine how much the velocity changes over the given path.
💡8 meters per second squared
This is the calculated value of acceleration, showing how quickly the velocity changes. The final step in the video involves confirming this result, ensuring the correct units and value for acceleration are obtained from the given data and calculations.
Highlights

Initial velocity given as 20 meters per second.

Final velocity is 60 meters per second.

The distance traveled is 200 meters.

The objective is to calculate acceleration.

Three kinematic equations are presented.

The chosen equation is v^2 = v₀^2 + 2aΔx.

The equation is rearranged to solve for acceleration.

Subtracting v₀^2 from both sides isolates the acceleration term.

Dividing by 2Δx gives the formula for acceleration.

Plugging in the given values to find acceleration.

Final velocity squared is calculated as 3600 m/s².

Initial velocity squared is 400 m/s².

The acceleration formula is simplified to a = (v² - v₀²) / (2Δx).

The calculated acceleration is 32 m/s² divided by 4.

The final acceleration result is 8 m/s².

The units of acceleration are confirmed as meters per second squared.

The process checks for the correct value and units of acceleration.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #32

AP Physics B Kinematics Presentation #03

Physics Lecture - 4 - Calculating Distance Traveled

Solving Three Acceleration Problems

AP Physics B Kinematics Presentation #34

Projectile Motion and Conservation of Energy - College Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsAccelerationKinematicsVelocitySpeedMotionProblem SolvingEducationalScienceMath