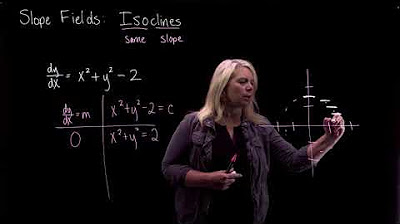Monday Night Calculus: Slope fields and differential equations
TLDRIn this engaging Monday Night Calculus session, hosts Curtis Brown and Tom Dick delve into the concept of slope fields and their application in understanding differential equations. The session is enriched by Steve Kakoska's insights, as they explore the relationship between the slope field of a differential equation and its corresponding solution curves. The presenters utilize a variety of examples to demonstrate how slope fields can provide a visual representation of the solutions to differential equations, offering strategies for sketching these fields and interpreting the behavior of the solutions. The session also touches on the use of technology in visualizing slope fields and emphasizes the importance of understanding the underlying mathematical concepts, rather than relying solely on computational tools. The interactive format encourages audience participation, fostering a deeper understanding of the material.
Takeaways
- 📚 The video is a part of a series called 'Monday Night Calculus' hosted by Curtis Brown, aimed at calculus students and teachers.
- 👥 The host is joined by Steve Kakoska and Tom Dick, who contribute their time and energy to prepare content for these sessions.
- 📝 The ti.edu website has a bulletin board post with previous recordings, a YouTube playlist, unique problem sets, and solutions for educators and students.
- 🎥 The session discusses slope fields, differential equations, and their applications, with a focus on visualizing solutions through slope fields.
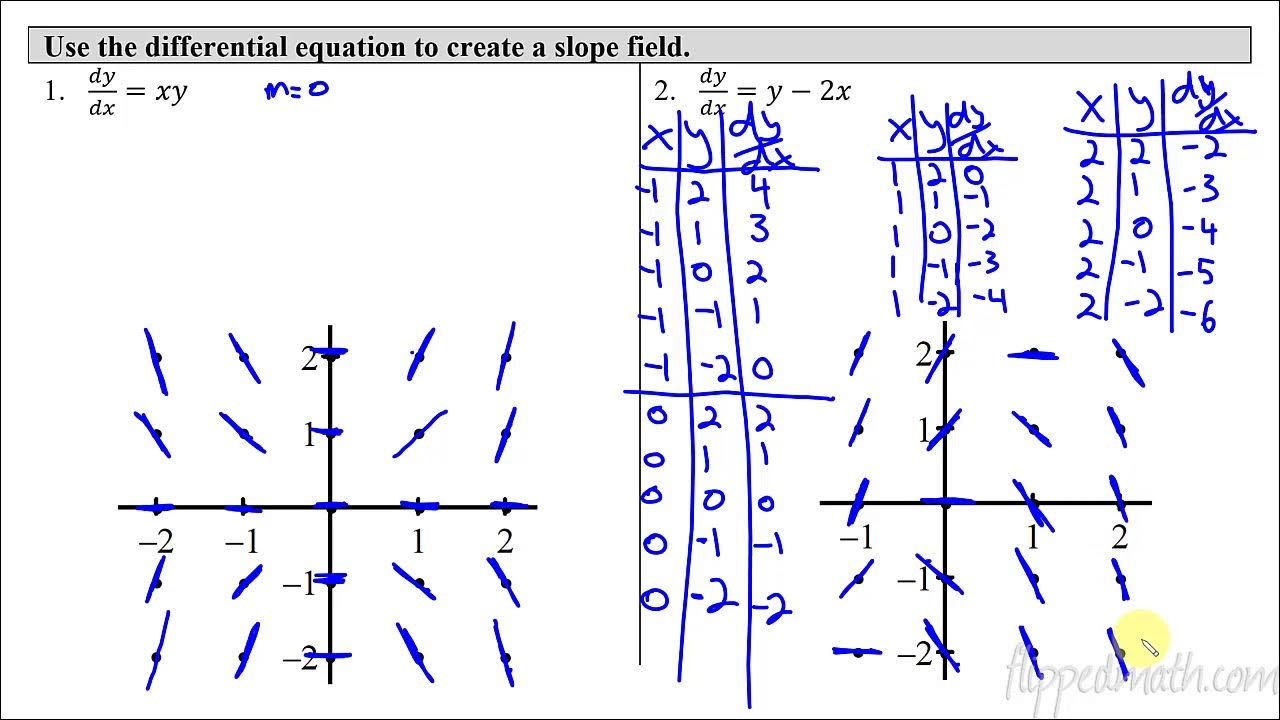
- 🌐 Slope fields provide a graphical display that shows the flow of tangent lines of solution curves, helping to visualize the general shape of these curves.
- 📱 The use of technology, such as the TI-Inspire, is encouraged for drawing slope fields, but it's also important to understand how to create them manually.
- 🔍 The video emphasizes the importance of understanding the context of a problem, especially when dealing with asymptotes and undefined values in differential equations.
- 📝 The session also covers how to solve first-order differential equations,分离变量法, and the introduction of constants of integration.
- 🤔 The concept of isoclines in slope fields is introduced as a tool for gaining insights into the structure of differential equations.
- 🌟 The video concludes with an exploration of how the arbitrary constant can manifest in different forms (horizontal shift, vertical shift, multiplicative factor) depending on the differential equation.
- 📅 The next 'Monday Night Calculus' session is scheduled to take place in two weeks, and both teachers and students are encouraged to participate.
Q & A
What is the main topic of the Monday Night Calculus video?
-The main topic of the Monday Night Calculus video is the exploration of slope fields and their relation to differential equations, including the discussion of how to sketch slope fields and solve differential equations.
Who are the hosts and guests in the video?
-The host of the video is Curtis Brown, and the guests are Steve Kakoska and Tom Dick.
What resource is mentioned for finding previous recordings of the calculus series?
-The resource mentioned for finding previous recordings is the TI Education website, specifically the bulletin board post on education.ti.com.
What type of problems are discussed in the video?
-The video discusses problems from a unique problem set created by Steve and Tom, which are designed for calculus students and teachers.
How does the concept of a slope field help in understanding differential equations?
-A slope field helps in understanding differential equations by providing a graphical representation that shows the flow of tangent lines of the solution curves, giving an idea of the general shape and nature of the solutions.
What is the significance of the arbitrary constant in the general solution of a differential equation?
-The arbitrary constant in the general solution of a differential equation represents the fact that there are infinitely many solutions to a given differential equation, and the constant allows for the specification of a unique solution when additional conditions, such as initial values, are provided.
How can the slope field be used to estimate the solution curve of a differential equation?
-The slope field can be used to estimate the solution curve by examining the slope of the tangent lines at various points on the graph, which gives an idea of the direction and shape of the solution curve.
What is an isocline and how does it help in analyzing a slope field?
-An isocline is a curve in a slope field where all the line segments have the same slope. It helps in analyzing a slope field by providing clues about the relationship between the variables in the differential equation and potentially simplifying the equation along these lines.
What is the role of technology in the teaching and understanding of slope fields?
-Technology plays a significant role in the teaching and understanding of slope fields by providing tools to visualize and interact with slope fields, making it easier to explore and analyze differential equations and their solutions.
What is Euler's method and how does it relate to slope fields?
-Euler's method is a numerical technique used to approximate solutions to differential equations. It relates to slope fields as it can be used to generate a sequence of points that approximate the solution curve, following the flow of the slope field.
Outlines
🎓 Introduction to Monday Night Calculus
The video begins with Curtis Brown, the host, welcoming viewers to another session of Monday Night Calculus. He expresses excitement about continuing the series of videos aimed at calculus students and teachers. Curtis introduces his guests, Steve Kakoska and Tom Dick, and appreciates their efforts in preparing content and problem sets for the session. He also mentions a bulletin board post on the TI Education website where viewers can access previous recordings, assignments, and unique problem sets with solutions. Curtis encourages viewers to participate by asking and answering questions in the chat. The session then transitions to addressing a question about slope fields and Euler's method, with Steve and Tom taking the lead in the discussion.
📚 Understanding Differential Equations and Slope Fields
Steve Kakoska takes over the presentation, clarifying that they will not be covering Euler's method that night but focusing on slope fields and differential equations. He explains that a differential equation is an equation containing an unknown function and its derivatives. Steve provides examples of differential equations and explains the concept of the order of a differential equation. He then discusses the idea of a solution to a differential equation, which is a function that satisfies the equation. Steve shares anecdotes from his graduate school days, highlighting the complexity of solving differential equations and the lack of a systematic method to solve all types. He introduces the concept of slope fields, which provide a graphical representation of the solutions to differential equations, allowing for a rough sketch of the solution curves. Tom Dick joins in, expressing his delight in seeing both teachers and students tuning in, and encourages viewers to ask questions.
📈 Visualizing Slope Fields and Solution Curves
Steve delves deeper into the concept of slope fields, explaining how they can be used to visualize the solution curves of differential equations. He uses the example of a first-order differential equation and explains how to sketch the graph of a solution curve using the slope field. Steve demonstrates how to interpret the differential equation and determine the slope of the tangent line at any point on the solution curve. He then creates a slope field for the given differential equation and uses it to estimate the solution curve. Tom contributes by discussing the introduction of slope fields into the AP Calculus curriculum and the initial anxiety it caused among teachers and students. He emphasizes that slope fields are not as complicated as they seem and that they can be a useful tool for visualizing the behavior of solutions.
🤔 Addressing Questions on Solution Curves and Slope Fields
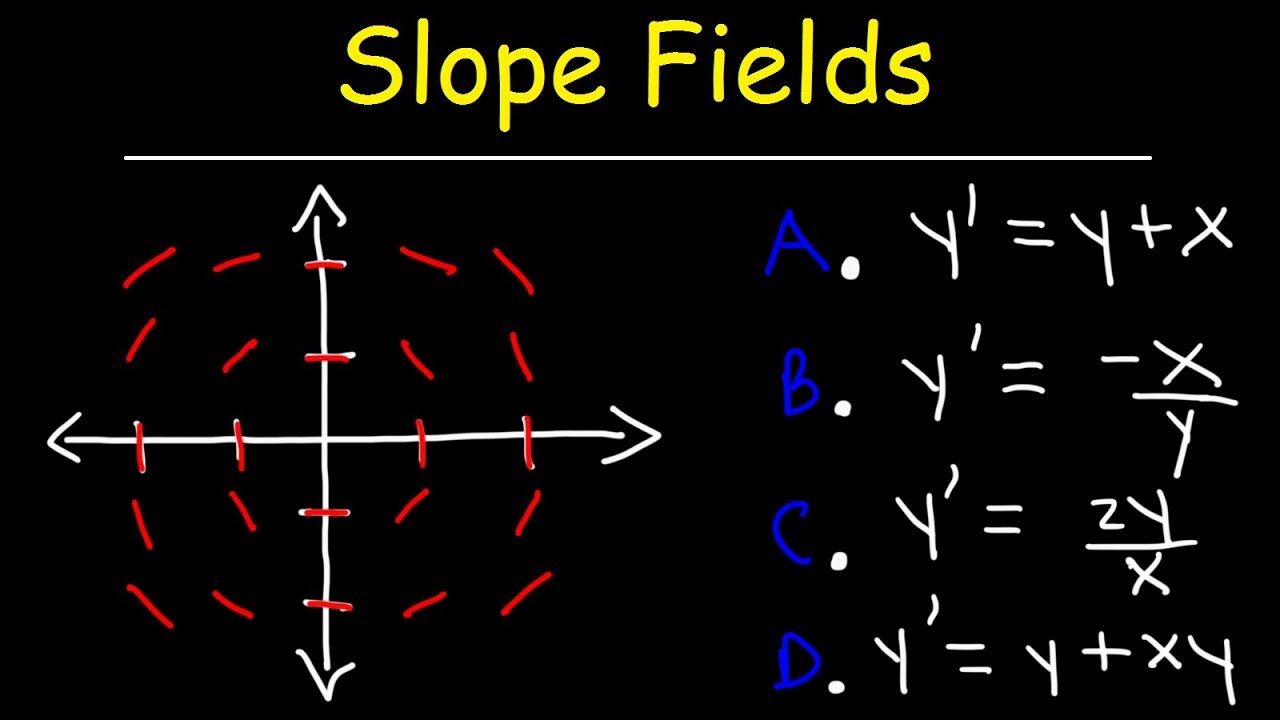
The discussion continues with Steve and Tom addressing questions about solution curves and slope fields. They talk about the possibility of solution curves crossing horizontal or vertical lines in the slope field and the implications of such intersections. Steve admits that they don't have a definitive answer to this question but suggests that the context of the problem is crucial in determining the behavior of the solution curve. Tom introduces the concept of isoclines in slope fields, which can provide additional insights into the nature of the solutions. They also discuss the process of matching slope fields to their corresponding differential equations and the importance of understanding the underlying trends in the slope field.
🧠 Strategies for Solving Differential Equations
Steve shares strategies for solving first-order differential equations, emphasizing the importance of recognizing trends in the slope field. He explains how to use these trends to infer the relationship between x and y in the differential equation. Steve provides a step-by-step approach to solving a differential equation, including separating variables, finding the antiderivative of both sides, and introducing a constant of integration. He also highlights the significance of using the initial condition effectively to find the particular solution. Tom adds his insights, discussing the role of technology in teaching calculus and the benefits of introducing slope fields early in the curriculum. He also talks about the impact of technology on the teaching and understanding of differential equations.
📊 Exploring Technology in Calculus Education
Tom takes the lead to discuss the role of technology in calculus education, particularly in the context of slope fields. He explains that while technology can be used to plot slope fields, the AP Calculus exam assesses students' understanding of slope fields through non-technology-based questions. Tom emphasizes the importance of understanding how slope fields are created and encourages teachers to introduce slope fields when teaching antiderivatives. He also shares his experience of using slope fields to explore the relationship between derivatives and original functions. Steve and Tom continue to discuss the nuances of differential equations, including the different roles the arbitrary constant can play in solutions.
🔧实操: 使用 TI-Nspire 绘制斜率场
Tom 展示如何在 TI-Nspire 上绘制斜率场,首先进入添加图形菜单,选择微分方程选项。他解释了如何输入微分方程(y1'=f(x,y1))并强调了在输入时需要注意 y 函数的具体命名(如 y1)。Tom 演示了如何调整斜率场的参数,例如场分辨率,以获得更精细的斜率场图形。他还提到了如何使用 TI-Nspire 绘制特定解的曲线,并通过调整参数来探索不同的解。此外,Tom 和 Steve 讨论了如何通过改变微分方程中的参数来观察斜率场的变化,以及如何使用滑块变量来影响微分方程的解。
🌐 结束语与鼓励参与
视频接近尾声时,Curtis 感谢 Steve 和 Tom 的精彩讨论,并鼓励观众参与进来。他提到观众可以通过聊天功能提问,并强调了学生参与的重要性。Curtis 提醒观众,未来还会有更多的 Monday Night Calculus 活动,并鼓励老师让学生参与进来。他还提到了 TI-Nspire 上的斜率场功能,并指出 TI-84 Plus CE 同样可以绘制斜率场,鼓励观众探索这一功能。最后,Curtis 以积极的态度结束了当晚的讨论,并期待下一次的见面。
Mindmap
Keywords
💡Calculus
💡Differential Equations
💡Slope Fields
💡Steve Kakoska
💡Tom Dick
💡Euler's Method
💡AP Calculus
💡Bulletin Board
💡Mark Corali
💡Technology in Education
Highlights
Introduction to Monday Night Calculus and the hosts Curtis Brown, Steve Kakoska, and Tom Dick.
Discussion on the bulletin board post on the TI Education website containing previous recordings, problem sets, and solutions.
Explanation of how to access the YouTube playlist with previous Monday Night Calculus recordings.
Introduction to the concept of slope fields and their importance in understanding differential equations.
Discussion on the anxiety surrounding the introduction of slope fields in the AP Calculus curriculum.
Explanation of differential equations, their order, and the challenges in finding solutions.
Illustration of how to sketch a solution curve using a slope field for a given differential equation.
Discussion on the process of solving a first-order differential equation with an initial value.
Demonstration of how to use the slope field to estimate the solution curve and its behavior.
Explanation of how the arbitrary constant in a general solution can lead to different types of solutions.
Discussion on the use of technology, specifically the TI-Nspire, in visualizing and understanding slope fields.
Presentation of a method to match a given slope field with its corresponding differential equation.
Discussion on the concept of isoclines in slope fields and how they can provide clues to the form of the differential equation.
Explanation of how to solve a first-order differential equation with an initial condition and the importance of using the initial condition correctly.
Discussion on the implications of the solution curve crossing horizontal or vertical lines in the slope field.
Conclusion and summary of the key points discussed during the Monday Night Calculus session.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: