2-D Vector Position & Velocity in Physics (Projectile Motion) - [1-4-1]
TLDRThis lesson delves into the concept of position and velocity in two and three dimensions, emphasizing the importance of understanding vector components for grasping motion along curved paths. By exploring the parabolic trajectory of a baseball and employing graphical illustrations, the instructor explains how to calculate average and instantaneous velocity, highlighting their vector nature and directional significance. The lesson builds a foundation for more advanced topics in physics, such as projectile motion and tensor analysis, and underscores the relevance of vector decomposition in comprehending motion dynamics.
Takeaways
- 📌 The concept of position and velocity in two dimensions is an extension of one-dimensional motion, essential for understanding more complex motion such as that of a baseball following a parabolic path.
- 📈 The average velocity in two dimensions is calculated as the change in position (vector) divided by the change in time (delta r / delta t), similar to one-dimensional motion but with vector components.
- 🎯 The instantaneous velocity is the limit of the average velocity as the time interval approaches zero, representing the velocity at a specific point in time and can be thought of as having x and y components.
- 🔄 The instantaneous velocity vector is always tangent to the path at the point of interest, indicating the direction of motion at that instant.
- 📐 The magnitude of the velocity vector (speed) can be found using the Pythagorean theorem (sqrt(v_x^2 + v_y^2)), and the direction is given by the inverse tangent of the y component divided by the x component.
- 🔢 The components of velocity can be calculated by considering the displacement in the x and y directions separately and dividing by the time interval.
- 🌐 The principles of position, velocity, and their components extend to three-dimensional space, with the addition of a z component to the position vector.
- 💡 Understanding the vector nature of position and velocity is crucial for grasping more advanced topics in physics, such as tensors and tensor analysis in relativity theory.
- 🚀 The motion of an object can be broken down into its components along different axes, which can then be analyzed separately to understand the overall motion.
- 📚 The lesson emphasizes the importance of not skipping over the theory, as it provides a solid foundation for understanding the equations and their applications in problem-solving.
Q & A
What is the main focus of this lesson?
-The main focus of this lesson is to understand position and velocity in two-dimensional and three-dimensional spaces, and how to calculate them using vectors.
How does the motion along a straight line differ from motion along a curve path?
-Motion along a straight line is simple and can be described by one-dimensional motion, while motion along a curve path, like a parabolic trajectory of a thrown baseball, involves two or three dimensions of motion and requires vector analysis to understand the position and velocity changes.
What is the significance of understanding vectors in physics?
-Understanding vectors is crucial in physics because they allow us to break down complex motions into simpler components, analyze them separately, and then combine them to understand the overall motion. This is essential for studying everything from projectile motion to planetary movements.
What is the difference between average velocity and instantaneous velocity?
-Average velocity is the overall speed of an object over a certain distance or time period, considering the start and end points. Instantaneous velocity, on the other hand, is the speed and direction of an object at a specific moment or point in its path.
How is the position vector used to represent the position of a point in two-dimensional space?
-A position vector is a straight line drawn from the origin to the point in question, with an arrowhead at the tip representing the location of the point. The length and direction of the vector represent the distance and angle from the origin to the point, respectively.
What is the Pythagorean theorem used for in the context of this lesson?
-The Pythagorean theorem is used to calculate the magnitude of a position vector, which represents the distance of a point from the origin in two-dimensional space. It is calculated by taking the square root of the sum of the squares of the x and y coordinates.
How can we find the average velocity of a point moving between two points in two-dimensional space?
-To find the average velocity, we subtract the initial position vector from the final position vector and then divide the resulting displacement vector by the time interval elapsed. This gives us a vector that represents the average velocity in both magnitude and direction.
What happens to the instantaneous velocity as the time interval approaches zero?
-As the time interval approaches zero, the displacement becomes infinitesimally small, but the time does as well, resulting in the instantaneous velocity at a specific point. This velocity is the limit of the displacement vector divided by the time interval as the interval approaches zero.
How can we describe the instantaneous velocity in terms of its components?
-The instantaneous velocity can be described in terms of its x and y components, which represent the horizontal and vertical velocities, respectively. These components can be found by considering the changes in the x and y coordinates over the time interval and dividing by the time interval.
What is the significance of the instantaneous velocity vector being tangent to the path at a point?
-The instantaneous velocity vector being tangent to the path at a point indicates the exact direction and speed of the object at that specific moment in time. It is the direction the object would continue to move in if all external forces were suddenly removed.
Outlines
📚 Introduction to Position and Velocity in 2D and 3D
The lesson begins with an introduction to the concepts of position and velocity in two and three dimensions, emphasizing the importance of understanding these concepts for grasping more complex topics like acceleration and projectile motion. The instructor shares a personal story to highlight the significance of comprehending the underlying principles rather than just memorizing equations.
📈 Understanding Average Velocity and Instantaneous Velocity
This section delves into the difference between average velocity, which considers the total displacement over a time interval, and instantaneous velocity, which examines the velocity at a specific point in time. The concept of breaking down motion into its components along the x and y axes is introduced, providing a foundation for analyzing curved paths such as a baseball's trajectory.
📊 Position Vectors and 2D Space
The lesson continues with a discussion on position vectors in two-dimensional space. The instructor explains how to represent a point's position with a vector arrow pointing to the origin and how the tip of this arrow indicates the coordinates of the point. The Pythagorean theorem is used to calculate the magnitude of the position vector, providing insight into the distance of the point from the origin and its direction.
🚀 Tracking Motion with Vectors
This part of the lesson focuses on using vectors to track the motion of an object, such as a baseball, over time. The instructor describes how the position vector changes as the object moves, with its length indicating distance and its angle indicating direction. The concept of a displacement vector is introduced, showing the change in position from the initial to the final point.
🌐 Components of Velocity
The instructor breaks down the concept of velocity into its horizontal and vertical components, explaining how these components can be calculated separately for any motion in two-dimensional space. The idea of a composite average velocity is also introduced, which is the combination of the individual x and y components, providing a complete picture of the object's motion.
🔄 Instantaneous Velocity and the Concept of Limits
The concept of instantaneous velocity is explored in detail, with the instructor explaining how it represents the velocity of an object at a specific instant in time. The idea of taking the limit as the time interval approaches zero is introduced, which is a fundamental concept in calculus and is used to find the instantaneous velocity at any given point.
📐 Graphical Representation of Instantaneous Velocity
The lesson concludes with a graphical demonstration of how to calculate instantaneous velocity. The instructor illustrates how to graphically subtract vectors to find the average velocity between two points and then refine this to find the instantaneous velocity as the time interval shrinks. The importance of understanding the direction and components of instantaneous velocity is emphasized, as it is always tangent to the path of the object.
Mindmap
Keywords
💡Position and Velocity
💡Two Dimensions
💡Acceleration
💡Vectors
💡Parabolic Path
💡Instantaneous Velocity
💡Projectile Motion
💡Tensors and Tensor Analysis
💡Average Velocity
💡Displacement Vector
Highlights
The lesson introduces the concept of position and velocity in two and three dimensions, moving beyond one-dimensional motion.
The parabolic path of a thrown baseball is discussed as an example of two-dimensional motion.
The importance of understanding vectors and their role in physics is emphasized for a comprehensive grasp of motion.
The lesson stresses the significance of not skipping the theory part even though equations are tempting to focus on.
The concept of average velocity in one dimension is reviewed as a foundation for understanding two-dimensional motion.
Instantaneous velocity is introduced as the limit of average velocity as time intervals approach zero.
The position vector is defined and its role in representing an object's position in space is discussed.
The method for calculating average velocity in two dimensions using vectors is explained through graphical representation.
The concept of vector components for x and y directions is introduced to break down complex motion into simpler parts.
The instantaneous velocity is described as being tangent to the path of motion at any given point.
The calculation of instantaneous velocity involves the concept of limits, which is foundational to calculus.
The lesson explains how to determine the x and y components of both average and instantaneous velocity.
The speed of an object is defined as the magnitude of the velocity vector, derived from the Pythagorean theorem.
The angle of the velocity vector is determined using the inverse tangent of the y component over the x component.
The lesson extends the discussion to three-dimensional space, explaining how position and velocity vectors work with x, y, and z components.
The importance of understanding the vector nature of motion is emphasized for solving complex physics problems.
The lesson concludes with an encouragement to review the material multiple times for better understanding and application.
Transcripts
Browse More Related Video
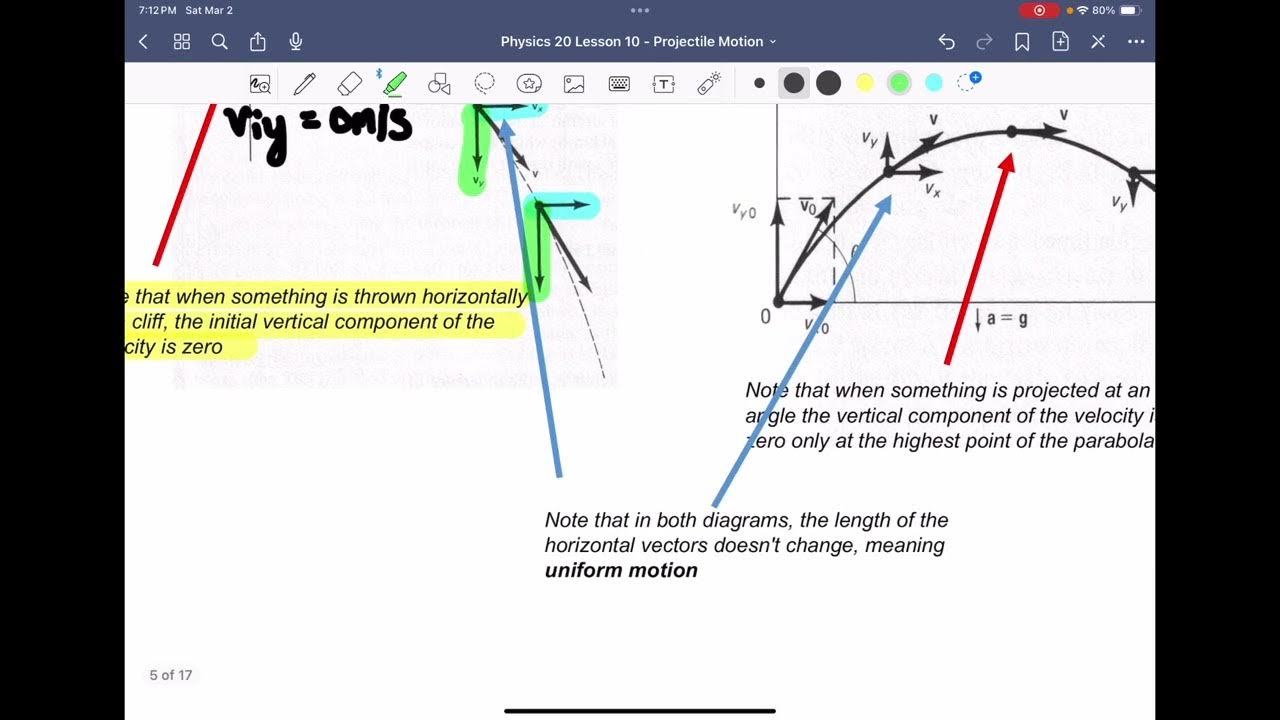
Physics 20 Unit A Lesson 10: Projectile Motion

17 - Calculating Vector Components in Physics, Part 1 (Component form of a Vector)
2. Vectors in Multiple Dimensions
Instantaneous Velocity in Physics - Formula, Definition & Examples - [1-2-5]

Calculus 3 Lecture 12.4: Velocity and Acceleration of Vector Functions

College Physics 1: Lecture 5 - Describing Motion
5.0 / 5 (0 votes)
Thanks for rating: