Instantaneous Velocity in Physics - Formula, Definition & Examples - [1-2-5]
TLDRThe lesson delves into the concept of instantaneous velocity and speed, differentiating them from average velocity. It explains how instantaneous velocity can be visualized and calculated using calculus, specifically derivatives and limits. The importance of understanding velocity as the derivative of position is emphasized, and the lesson illustrates this with examples, including a particle's motion described by a parabolic function. The relationship between the slope of the position function's tangent line and the velocity is clarified, providing a foundation for further physics and engineering studies.
Takeaways
- 🌟 The concept of instantaneous velocity is introduced as a vital part of understanding motion in physics, distinct from average velocity.
- 🚀 Instantaneous velocity can be thought of as the velocity of an object at a specific moment in time, as opposed to the average velocity over a period of time.
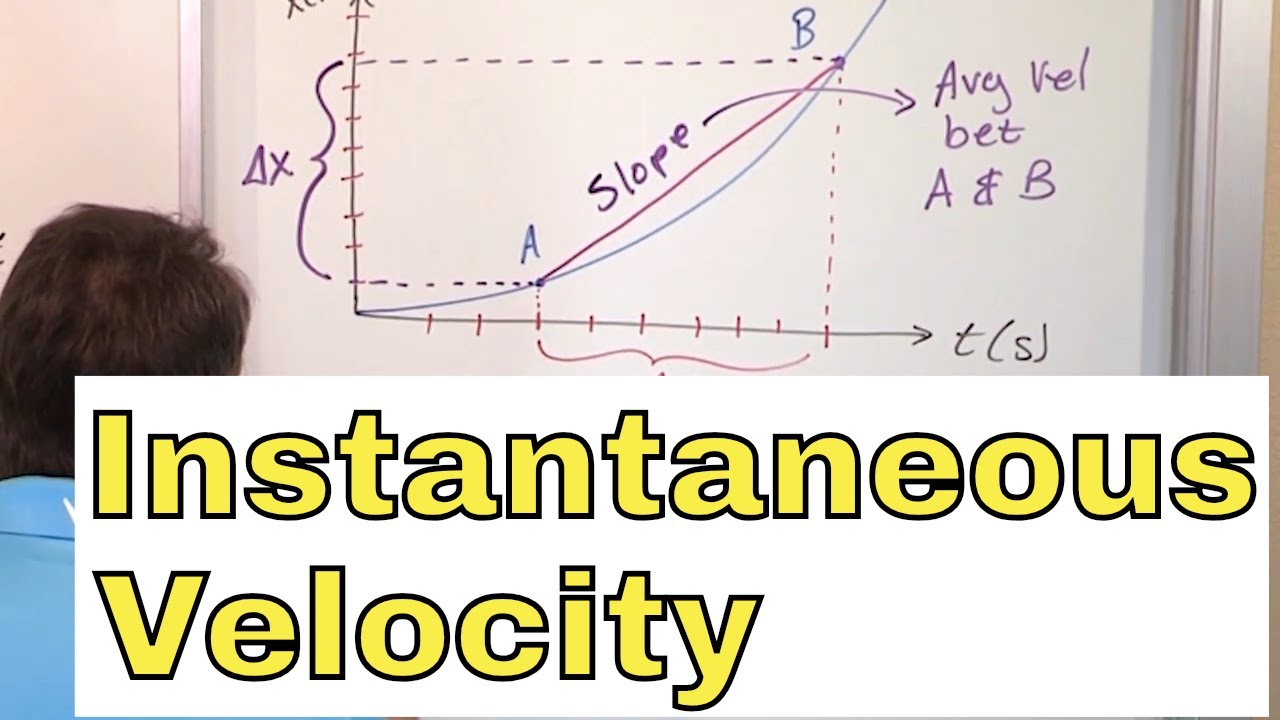
- 📈 The mathematical representation of instantaneous velocity is given by the limit of the ratio of change in position (Δx) to the change in time (Δt) as Δd approaches zero, denoted as v = lim(Δt->0) [Δx/Δt].
- 🛤️ The instantaneous velocity is visualized on a graph by finding the slope of the tangent line to the position-time curve at a particular point, which represents the velocity at that instant.
- 📚 The process of finding the instantaneous velocity involves taking the derivative of the position function with respect to time, which yields the velocity function.
- 🔄 The concept of limits and derivatives in calculus is fundamental to calculating instantaneous velocity, as it allows us to find the rate of change of position with respect to time.
- 🎯 The velocity of a particle is the derivative of its position with respect to time, a principle that is universally applicable in physics, engineering, and mathematics.
- 🛤️ The average velocity between two points on a graph is the slope of the line connecting those points, while the instantaneous velocity is the limit of this slope as the time interval shrinks to zero.
- 📊 The direction of the velocity (positive or negative) is determined by the sign of the slope of the tangent line at a point on the position-time graph, indicating whether the object is moving towards a positive or negative direction.
- 🔢 The instantaneous speed is the magnitude of the instantaneous velocity, which is the absolute value of the velocity and does not include directional information.
Q & A
What is instantaneous velocity and how is it different from average velocity?
-Instantaneous velocity is the velocity of an object at a specific moment in time, unlike average velocity which calculates the rate of change in position over a defined interval of time. Instantaneous velocity considers the limit as the time interval approaches zero, effectively capturing the velocity at a precise instant.
How is instantaneous velocity calculated using calculus?
-Instantaneous velocity is calculated as the limit of the change in position (delta x) over the change in time (delta t) as delta t approaches zero. Mathematically, it's the derivative of the position function with respect to time, represented as dx/dt.
Why is the concept of instantaneous velocity important in physics?
-Instantaneous velocity is crucial in physics because it provides a precise measurement of an object's velocity at any given moment, allowing for the analysis of dynamic systems where speed and direction may change over time. This concept is fundamental for understanding motion and applying the principles of mechanics accurately.
What does the process of finding the instantaneous velocity involve?
-Finding instantaneous velocity involves taking two points on the curve of an object's motion path, bringing these points infinitesimally close together, and calculating the slope of the tangent line at this point. This process utilizes the limit concept in calculus, effectively determining the object's velocity at a specific instant.
How can one visualize instantaneous velocity on a graph?
-On a graph, instantaneous velocity can be visualized as the slope of the tangent line to the curve at a specific point. This line represents the rate of change of position at that precise moment, providing a graphical representation of an object's instantaneous speed and direction.
What is the significance of the derivative in the context of instantaneous velocity?
-The derivative, in the context of instantaneous velocity, signifies the rate of change of position with respect to time. It mathematically represents the concept of instantaneous velocity, allowing us to calculate the velocity at any given point along an object's path of motion.
What does the notation dx/dt represent in physics?
-In physics, the notation dx/dt represents the derivative of position (x) with respect to time (t), indicating the instantaneous velocity of an object. It signifies the infinitesimally small change in position over an infinitesimally small interval of time.
How does one differentiate between velocity and speed in the context of instantaneous measurements?
-In the context of instantaneous measurements, velocity is a vector quantity that includes both magnitude and direction, while speed is a scalar quantity that represents only the magnitude. Instantaneous speed is the absolute value of instantaneous velocity, indicating how fast an object is moving regardless of its direction.
Why is it necessary to bring two points 'infinitesimally close' to each other when calculating instantaneous velocity?
-Bringing two points 'infinitesimally close' is necessary to calculate instantaneous velocity because it allows for the measurement of velocity at a specific instant, rather than over an interval. This method uses calculus to approximate the points as nearly overlapping, facilitating the calculation of the slope of the tangent line at a precise point on the curve.
Can the concept of instantaneous velocity be applied to any type of motion?
-Yes, the concept of instantaneous velocity can be applied to any type of motion, whether linear, circular, or any other path. It provides a detailed understanding of how an object's velocity changes at each moment, essential for analyzing complex movements in physics.
Outlines
🌟 Introduction to Instantaneous Velocity
The video begins with an introduction to the concept of instantaneous velocity and speed, emphasizing its importance in physics. The instructor explains that instantaneous velocity differs from average velocity as it represents the velocity of an object at a specific instant in time, rather than over a period. The lesson aims to build upon the understanding of average velocity from previous lessons and introduce the mathematical tools of calculus, specifically derivatives and limits, to calculate instantaneous velocity. The goal is to not only define instantaneous velocity but also to visualize it on a graph and calculate it using calculus.
📈 Derivation of Instantaneous Velocity
This paragraph delves into the mathematical derivation of instantaneous velocity. The instructor explains that instantaneous velocity is found by taking the limit of the change in position (delta x) divided by the change in time (delta t) as the time interval approaches zero. This process is visually demonstrated by shrinking the time intervals on a graph until two points coincide, effectively finding the slope of the tangent line at a single point on the position-time graph. The instructor emphasizes that this slope represents the instantaneous velocity and introduces the concept of the derivative of position with respect to time, which is the fundamental idea of the lesson.
🚀 Understanding Velocity through Examples
The instructor uses the example of a rocket launch to illustrate the concept of instantaneous velocity. The discussion covers how the velocity of the rocket changes over time, from being almost zero at the launch pad to increasing rapidly as it ascends. The idea of bringing two points on the graph closer together to find the velocity at a precise instant is further explained. The paragraph concludes with a graphical representation of how the velocity changes throughout the rocket's trajectory, emphasizing the importance of understanding the derivative of position with respect to time as the key to calculating instantaneous velocity.
📊 Graphical Representation and Calculation
The instructor provides a detailed explanation of how to graphically represent and calculate instantaneous velocity. Using the position-time graph, the concept of the slope of the line connecting two points and how it relates to average velocity is discussed. The process of bringing a second point closer to the first to find a better approximation of instantaneous velocity is demonstrated. The concept of a tangent line, which touches the curve at a single point, is introduced as the method to find the instantaneous velocity. The paragraph concludes with the mathematical representation of instantaneous velocity as the limit of delta x over delta t as delta t approaches zero, and the renaming of this process in calculus as dx/dt.
🔄 Velocity and Direction
This paragraph focuses on the direction of velocity and introduces the concept of instantaneous speed. The instructor explains that velocity is a vector quantity, meaning it has both magnitude and direction, while speed is the magnitude of velocity without regard to direction. The discussion includes how to determine the sign of velocity based on the slope of the tangent line at a point on the position-time graph. The paragraph also covers how to calculate instantaneous speed by taking the absolute value of the velocity. The importance of understanding the sign of velocity in determining the direction of motion is emphasized.
🧠 Practical Application: Calculating Instantaneous Velocity
The instructor presents a practical example of calculating instantaneous velocity using a given position function. The example involves a particle moving along a parabolic path, and the position function is given as x = t^2. The derivative of this function with respect to time is calculated to find the velocity function, which is 2t. The velocity at various time intervals is then determined and tabulated. The paragraph concludes with a discussion on how the velocity increases over time and how this is reflected in the graph of the velocity function, showing a constant rate of acceleration.
🎯 Summary and Future Applications
The final paragraph summarizes the key points of the lesson, reinforcing the understanding of instantaneous velocity as the derivative of the position function with respect to time. The process of finding instantaneous velocity by taking the limit of delta x over delta t as the time interval becomes infinitesimally small is reiterated. The paragraph also reviews the concepts of average velocity, the graphical representation of velocity through the slope of the tangent line, and the distinction between velocity and speed. The instructor encourages further practice and application of these concepts in future lessons to solidify understanding and apply them to problems in physics.
Mindmap
Keywords
💡Instantaneous Velocity
💡Average Velocity
💡Derivative
💡Limit
💡Position Function
💡Slope
💡Acceleration
💡Tangent Line
💡Physics
💡Calculus
Highlights
Introduction to instantaneous velocity and speed, merging calculus with physics concepts.
Average velocity defined as the distance traveled over time, setting the groundwork for instantaneous velocity.
Instantaneous velocity introduced as a key concept in physics, described through the imagery of a rocket's acceleration.
Mathematical formulation of instantaneous velocity using limits, making calculus applicable to physics.
Visualization of average vs. instantaneous velocity using slopes of secant and tangent lines on a graph.
Conceptual transition from average to instantaneous velocity, emphasizing the limit process in calculus.
The derivative as a fundamental tool for calculating instantaneous velocity, linking mathematics closely with physics.
Velocity as the derivative of position, a pivotal idea in both physics and calculus.
Practical application of calculating instantaneous velocity through a series of graphical examples.
Detailed exploration of motion using position-time graphs to intuitively understand velocity changes.
Differentiating between velocity and speed, and introducing the concept of instantaneous speed.
Velocity's dependency on the direction of motion, with speed representing the magnitude of velocity.
Concrete example demonstrating the application of calculus to determine a particle's velocity from its position function.
Reiteration of the importance of the derivative for finding velocity, emphasizing continuous learning in calculus.
Final summary underscoring the lesson's goal to elucidate the concept of instantaneous velocity and its calculation.
Transcripts
Browse More Related Video
07 - What is Instantaneous Velocity?, Part 1 (Instantaneous Velocity Formula & Definition)

Average/Instantaneous Rates of Changes

AP Daily: AP Calculus BC (1.1)

College Physics 1: Lecture 7 - Instantaneous Velocity

8.01x - Lect 2 - 1D Kinematics - Speed, Velocity, Acceleration

Intro to Derivatives, Limits & Tangent Lines in Calculus | Step-by-Step
5.0 / 5 (0 votes)
Thanks for rating: