Range Equation Derivation

Olga Andreeva
26 Jan 201507:44
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delivers a clear and methodical explanation of how to derive the range equation from the horizontal and vertical components of motion equations. It begins by decomposing the initial velocity into its x and y components, then utilizes the horizontal and vertical motion equations to solve for the range. The derivation cleverly employs trigonometric identities, particularly sine 2θ, to arrive at the final form of the range equation, demonstrating the relationship between initial velocity, gravity, and the angle of projection.

Takeaways
  • 📚 The range equation is derived from the horizontal and vertical components of motion equations.
  • 🚀 Initial velocity is broken down into its x (vx) and y (vy) components using sine and cosine of the launch angle (theta).
  • 🧭 The horizontal equation is delta x equals v_initial times delta t, while the vertical equation includes acceleration (gravity) in its calculation.
  • 🔄 The range equation only works when there is no change in height, meaning the projectile does not gain or lose altitude.
  • 🌐 The vertical component (vy) is calculated as v_initial times sine of theta, and the horizontal component (vx) as v_initial times cosine of theta.
  • 🔢 By solving the vertical equation for delta t and substituting into the horizontal equation, we can express range (delta x) in terms of the initial velocity and launch angle.
  • 📈 The derived range equation is delta x equals v_initial squared times sine 2 theta over the acceleration due to gravity.
  • 🌟 A trigonometric property simplifies the equation, where cosine theta times sine theta times 2 equals sine 2 theta.
  • 🎯 In projectile motion problems, the acceleration is considered as gravity, which always acts downwards towards the ground.
  • 📊 The final simplified range equation is delta x equals v_initial squared times sine 2 theta over gravitational acceleration, which is fundamental for analyzing projectile motion.
Q & A

  • What is the formula for range in the context of projectile motion?

    -The formula for range (delta x) in the context of projectile motion is given by: delta x = (v_initial^2 * sin(2 * theta)) / gravity.

  • How is the initial velocity broken down in the analysis of projectile motion?

    -The initial velocity is broken down into its horizontal (vx) and vertical (vy) components. vx = v_initial * cos(theta) and vy = v_initial * sin(theta), where theta is the launch angle.

  • What are the standard horizontal and vertical motion equations used in the derivation of the range equation?

    -The standard horizontal motion equation is delta x = v_initial * delta t, and the vertical motion equation is delta y1 = v_initial * delta t + (1/2) * acceleration * (delta t)^2.

  • Why is the change in height (delta y) set to zero in the derivation of the range equation?

    -The change in height (delta y) is set to zero because the range equation only works when there is no change in height, which means the projectile is launched from and returns to the same height.

  • How does the direction of gravity affect the acceleration term in the vertical motion equation?

    -The direction of gravity affects the acceleration term as a negative value because gravity acts downwards, which is considered the negative direction when 'up' is defined as positive.

  • What is the significance of the trigonometric identity used in simplifying the range equation?

    -The trigonometric identity cos(theta) * sin(theta) * 2 equals sin(2 * theta) is used to simplify the range equation, making it more concise and easier to understand.

  • Why is acceleration considered as gravity in the context of projectile motion problems?

    -In projectile motion problems, the only acceleration acting on the object is due to gravity, which is always directed downwards towards the ground. Hence, acceleration is considered equal to the acceleration due to gravity.

  • How does the horizontal component of velocity (vx) affect the range of the projectile?

    -The horizontal component of velocity (vx) directly influences the range as it is multiplied by the time of flight (delta t) in the range equation. A larger horizontal velocity component results in a longer time of flight and thus a greater range.

  • What is the role of the launch angle (theta) in determining the range of a projectile?

    -The launch angle (theta) is crucial in determining the range as it affects both the horizontal and vertical components of the initial velocity. The range is directly proportional to the sine of twice the launch angle, meaning that certain angles (like 45 degrees or pi/4 radians) will maximize the range.

  • How does the initial velocity (v_initial) impact the range of the projectile?

    -The initial velocity (v_initial) has a significant impact on the range as it appears in the numerator of the range equation. An increase in the initial velocity will result in an increase in the range, assuming other factors such as gravity and the launch angle remain constant.

  • What is the relationship between the horizontal and vertical components of velocity in the context of projectile motion?

    -The horizontal and vertical components of velocity are related through the launch angle and the initial velocity. They are derived from the initial velocity using trigonometric functions, with the horizontal component (vx) being the product of the initial velocity and the cosine of the launch angle, and the vertical component (vy) being the product of the initial velocity and the sine of the launch angle.

Outlines
00:00
🔢 Deriving the Range Equation

This section explains the process of deriving the range equation used in projectile motion problems by breaking down the initial velocity into its horizontal and vertical components. The narrator begins by introducing the known range equation, Δx = v_initial^2 * sin(2θ) / g, and proceeds to explain how to derive it from basic principles. This involves decomposing the initial velocity (v_initial) into its x (vx) and y (vy) components using trigonometric functions, specifically sine and cosine in relation to the angle θ. The equations for horizontal and vertical motion are then employed to express the range (Δx) in terms of time (Δt) and acceleration due to gravity. An error in variable naming is corrected, emphasizing the importance of distinguishing between the components of velocity (vx and vy) when applying these equations. The narrator clarifies the conditions under which the range equation applies, specifically when there is no change in vertical position (Δy = 0), and how to manipulate the equations to solve for the time variable, which is then used to derive the final form of the range equation.

05:04
📐 Simplifying the Range Equation

In this part, the video script continues with the simplification of the derived range equation. The narrator explains how to integrate the previously determined components of velocity and time into the formula for range (Δx). By substiting vx and Δt into the range equation, they show the mathematical process that leads to the simplification of the equation, using trigonometric identities to further condense the formula. This process results in the final simplified range equation, Δx = v_initial^2 * sin(2θ) / g, which mirrors the initially presented range equation but is arrived at through a comprehensive derivation process. The narrator emphasizes the applicability of this equation to projectile motion problems where gravity is the sole acceleration, reinforcing the concept that this formula is specifically tailored for scenarios where the projectile's vertical position does not change.

Mindmap
Keywords
💡Range Equation
The Range Equation is a fundamental formula used in physics to calculate the horizontal distance (range) that a projectile will travel before landing. In the context of the video, it is derived from the horizontal and vertical components of motion equations, and it is represented as delta x equals initial velocity squared times sine of 2 times theta, divided by gravity. This equation is crucial for understanding projectile motion and how it can be applied to various real-world scenarios, such as launching a ball or a missile.
💡Horizontal and Vertical Components
In projectile motion analysis, the initial velocity is decomposed into horizontal (vx) and vertical (vy) components. This decomposition allows for the separate study of the motion in each direction, considering factors such as gravity's effect on the vertical motion and the absence of resistance in the horizontal motion. In the video, these components are used to derive the Range Equation, with vx calculated as the initial velocity times cosine of theta and vy as the initial velocity times sine of theta.
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. In the context of the video, trigonometric functions like sine and cosine are used to break down the initial velocity into its horizontal and vertical components, which are essential for deriving the Range Equation. The script also mentions the trigonometric property that cosine times sine of two times an angle is equal to sine of that angle, which simplifies the final equation.
💡Projectile Motion
Projectile Motion refers to the motion of an object that is launched into the air and moves under the influence of gravity and air resistance (if considered). It is a type of motion that has both horizontal and vertical components, which can be analyzed separately due to the absence of forces in the horizontal direction (ignoring air resistance). The video focuses on deriving the Range Equation, which is a key formula in the study of projectile motion, and explains how the motion can be broken down into horizontal and vertical components for analysis.
💡Acceleration
In physics, acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity that has both magnitude and direction. In the context of the video, acceleration, particularly gravitational acceleration, is considered as the constant acceleration due to gravity that acts vertically downwards. This acceleration is a key factor in the vertical motion of a projectile and is used in the equations to derive the Range Equation.
💡Initial Velocity
Initial Velocity is the speed at which an object begins its motion. In the context of projectile motion, it is the velocity with which the object is launched or thrown. The initial velocity is a crucial parameter in the analysis of projectile motion as it determines the speed and direction of the object at the beginning of its trajectory. The video script explains how the initial velocity is broken down into its horizontal and vertical components to derive the Range Equation.
💡Delta X (Range)
Delta X, often referred to as the Range, is the horizontal distance that a projectile travels from its point of launch to the point where it lands. It is the primary focus of the Range Equation and is calculated using the initial velocity, the angle of projection, and the acceleration due to gravity. The video script provides a detailed derivation of how Delta X is calculated using the horizontal and vertical components of motion.
💡Sine and Cosine
Sine and cosine are two of the six trigonometric functions that relate the angles and sides of a right-angled triangle. In the context of the video, sine and cosine are used to calculate the vertical (vy) and horizontal (vx) components of the initial velocity, respectively. These functions are essential in the derivation of the Range Equation and the analysis of projectile motion.
💡Derivation
In mathematics, derivation refers to the process of obtaining a result or a formula from a set of known principles or assumptions through logical reasoning and mathematical manipulation. The video script focuses on the derivation of the Range Equation from the basic principles of projectile motion, using trigonometry and the equations of motion.
💡Equations of Motion
Equations of Motion are mathematical formulas that describe the motion of an object under the influence of various forces. In the context of the video, the horizontal and vertical equations of motion are used to analyze the motion of a projectile, with the horizontal equation relating Delta X to the initial velocity and time, and the vertical equation relating Delta Y to the initial velocity, time, and acceleration. These equations are crucial for deriving the Range Equation and understanding the behavior of projectiles.
💡Gravitational Acceleration
Gravitational Acceleration, often denoted by 'g', is the acceleration experienced by objects due to the gravitational pull of the Earth. Its value is approximately 9.81 m/s^2 near the Earth's surface. In the context of the video, gravitational acceleration is the constant acceleration that affects the vertical motion of a projectile and is used in the equations to derive the Range Equation.
Highlights

Derivation of the range equation from horizontal and vertical motion equations.

Breaking down initial velocity into x and y components using sine and cosine of theta.

The horizontal equation: delta x equals v initial times delta t.

The vertical equation: delta y1 is v initial times delta t plus one half acceleration times delta t squared.

Rewriting the vertical equation to solve for delta t in terms of delta y and acceleration.

Simplifying the equation by dividing by one half acceleration and expressing delta t in terms of initial velocity and sine of theta.

Using the horizontal equation to express delta x in terms of vx, which is cosine theta times v initial.

Substituting the derived expression for delta t into the horizontal equation to find delta x.

Simplifying the range equation by canceling out the common factor of initial velocity.

Utilizing the trigonometric identity of cosine theta times sine theta times two equals sine two theta to further simplify the range equation.

The final form of the range equation: delta x equals initial velocity squared times sine 2 theta over acceleration (gravity).

The importance of the reference point in determining the positive or negative sign of acceleration in the equations.

The condition for the range equation to be valid: no change in height (delta y must be zero).

The practical application of the range equation in projectile motion problems where gravity acts downwards.

The method for deriving the range equation is applicable to various projectile motion scenarios.

The significance of understanding both horizontal and vertical components of motion to accurately derive and apply the range equation.

Transcripts

Browse More Related Video

Where Does The Range Equation Come From?

Deriving the Range Equation of Projectile Motion

AP Physics B Kinematics Presentation #74

Why Does 45º Launch Angle Give Maximum Range? // HSC Physics

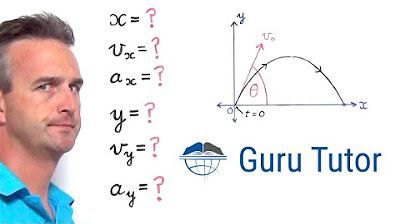
Deriving the 6 Basic Projectile Motion Equations

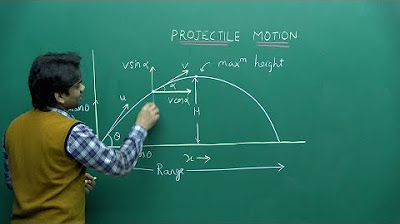
NEET Physics | Projectile Motion | Theory & Problem-Solving | In English | Misostudy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysics EducationEquation DerivationTrigonometryKinematicsMechanicsHorizontal RangeTeaching AidScience LearningMathematical Analysis