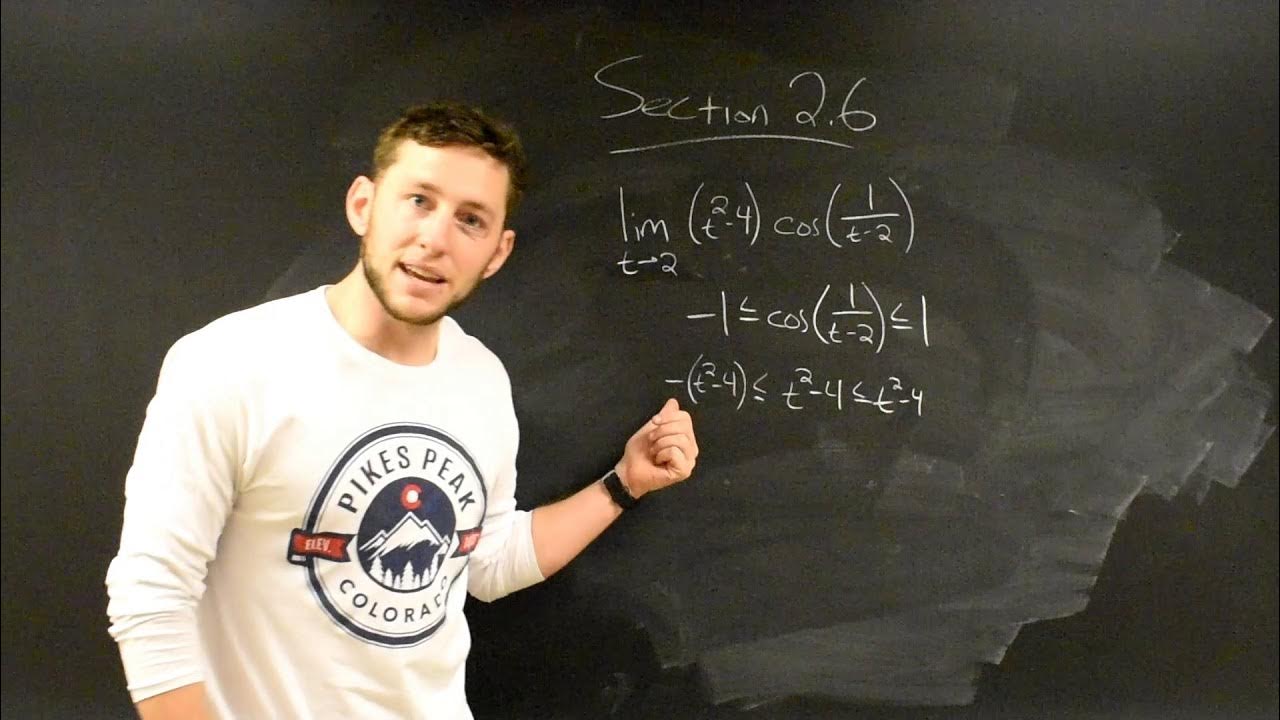Limits and Continuity
TLDRThe video script presents a series of mathematical problems involving limits, focusing on various techniques such as direct substitution, factoring, and the use of trigonometric identities. It covers the evaluation of limits for rational functions, complex fractions, and the application of the intermediate value theorem. The video also explains how to find horizontal asymptotes and apply the squeeze theorem. Each problem is methodically solved, leading to the correct answer choice, which is then cross-referenced with provided options, enhancing the viewer's understanding of limit concepts and problem-solving strategies in calculus.
Takeaways
- 📝 Direct substitution can be used to evaluate limits when the substitution does not result in a zero in the denominator.
- 🔍 Factoring is essential when direct substitution results in a zero in the denominator, allowing for cancellation and simplification.
- 🌟 Complex fractions are simplified by multiplying both the numerator and the denominator by the common denominator.
- 📊 Rational functions with square roots in the numerator can be simplified by multiplying both the numerator and the denominator by the conjugate of the numerator.
- 🚫 Limits that result in an indeterminate form require checking the left and right-sided limits for their values.
- 📈 Trigonometric limits can be found by simplifying the expression and applying known limit formulas, such as the limit of sine divided by its argument as it approaches zero.
- 🏞 Horizontal asymptotes are determined by evaluating the limit as x approaches infinity, identifying the dominant terms in the expression.
- 📉 The Squeeze Theorem is a powerful tool for determining limits when a function is bounded between two others that approach the same limit.
- 🔄 The Intermediate Value Theorem ensures the existence of a root within a closed interval if the function is continuous and the function values at the interval endpoints are different.
- 🔧 To make a function continuous at a specific point, the limits from both sides of the point must be equal to the function value at that point.
Q & A
What method is suggested for solving the first problem in the video quiz?
-Direct substitution is suggested for the first problem since plugging in the value of 2 avoids a zero in the denominator of the fraction.
What is the correct answer for the first problem based on the video quiz?
-The correct answer for the first problem is answer choice B, as the limit value is found to be 6.
Why can't direct substitution be used for the second problem in the video quiz?
-Direct substitution cannot be used for the second problem because it results in a zero in the denominator, which is undefined.
How is the second problem's limit evaluated in the video quiz?
-The second problem's limit is evaluated by factoring the numerator and denominator, canceling out common terms, and then substituting the value of x to find the simplified quotient.
What is the correct answer for the second problem according to the video quiz?
-The correct answer for the second problem is answer choice D, as the simplified limit expression results in 4/3.
How does the video quiz approach the calculation of the third problem's limit?
-The third problem's limit is calculated by multiplying the numerator and denominator by the common denominator, simplifying the expression, and then evaluating the limit as x approaches the given value.
What is the final answer for the third problem in the video quiz?
-The final answer for the third problem is answer choice C, which is -1/16, obtained through direct substitution after simplifying the expression.
What technique is used in the video quiz to find the value of the limit for the rational function with a square root in the numerator?
-The technique used is multiplying the numerator and denominator by the conjugate of the numerator, simplifying the expression, and then canceling out terms to find the limit as x approaches the given value.
What is the correct answer for the fourth problem in the video quiz?
-The correct answer for the fourth problem is answer choice A, as the limit simplifies to 1/8 after applying the technique described.
How does the video quiz address the indeterminate form in the fifth problem?
-The video quiz addresses the indeterminate form by checking both the left-sided and right-sided limits. Since they do not match, the limit does not exist, leading to the selection of answer choice E.
What trigonometric identity is used to simplify the sixth problem in the video quiz?
-The identity used to simplify the sixth problem is the limit of sine y divided by y as y approaches zero, which is equal to 1. This is used to find the limit of the given trigonometric function.
What is the correct answer for the sixth problem, and why is it chosen?
-The correct answer for the sixth problem is answer choice B, which is 3/5. It is chosen because the limit of the trigonometric function simplifies to this value using the mentioned identity.
How does the video quiz determine the horizontal asymptote for the function in the seventh problem?
-The horizontal asymptote is determined by evaluating the limit as x approaches infinity, considering the dominating terms in the numerator and denominator, and simplifying to find the constant ratio.
What is the equation of the horizontal asymptote for the function in the seventh problem?
-The equation of the horizontal asymptote is y equals nine, as the limit simplifies to the constant value nine when x approaches infinity.
How does the video quiz apply the Squeeze Theorem in the eighth problem?
-The Squeeze Theorem is applied by showing that the function f(x) = sin(1/x) is between negative x and positive x as x approaches zero, and since the limits of h(x) = -x and g(x) = x as x approaches zero are both zero, it is concluded that the limit of f(x) must also be zero by the theorem.
What is the correct answer for the eighth problem based on the Squeeze Theorem?
-The correct answer for the eighth problem is answer choice B, as the Squeeze Theorem confirms that the limit of the function as x approaches zero must be zero.
What conditions must be met for the Intermediate Value Theorem to apply, as discussed in the ninth problem?
-For the Intermediate Value Theorem to apply, the function f must be continuous on the closed interval a to b, and f(a) must not equal f(b). There must exist a number k between f(a) and f(b) such that f(c) equals k, and c must be in the interval of a and b.
What value of c is found using the Intermediate Value Theorem for the ninth problem?
-Using the Intermediate Value Theorem, the value of c is found to be 1, since it's the value in the interval [0, 2] for which f(c) equals the k value of zero, as per the theorem's conditions.
How is the value of c determined to make the function continuous at x equals two in the tenth problem?
-The value of c is determined by setting the two given functions equal to each other at x equals two, simplifying the resulting equation, and solving for c, which is found to be 3.
What is the correct answer for the tenth problem, and what is the value of c?
-The correct answer for the tenth problem is answer choice C, with the value of c being 3, which makes the function continuous at x equals two.
Outlines
📝 Solving Limits through Direct Substitution and Factoring
This paragraph introduces a video quiz focused on solving limit problems. The first problem involves direct substitution to find the limit as x approaches 2, where the function is 2 squared plus 7 times 2 plus 6 divided by 2 plus 2. By calculating the numerator and denominator separately and dividing, the limit is found to be 6. The second problem requires factoring to avoid division by zero. The numerator factors to (x + 5)(x - 3), and the denominator factors to (x + 3)(x - 3), with the limit evaluated as x approaches 3, resulting in 4/3. The third problem involves simplifying a complex fraction by multiplying the numerator and denominator by the common denominator, 4x, and canceling terms to find the limit as x approaches 4, which is -1/16. The fourth problem deals with a rational function involving a square root, where the limit is found by multiplying the numerator and denominator by the conjugate of the numerator and simplifying, yielding 1/8.
🔢 Evaluating Limits with Trigonometric Functions and Asymptotes
The second paragraph continues the video quiz with more limit problems. The fifth problem involves evaluating a limit where direct substitution is not possible due to an indeterminate form. By examining the left and right limits as x approaches 7, it is determined that the limit does not exist. The sixth problem focuses on a trigonometric function, where the limit is found to be 3/5 by replacing tangent with sine divided by cosine and simplifying. The seventh problem discusses finding the horizontal asymptote of a function by evaluating the limit as x approaches infinity, which in this case is y equals nine. The eighth problem examines the behavior of the sine function as x approaches zero, using the squeeze theorem to determine that the limit of sine(1/x) as x approaches zero is zero.
📈 Applying the Intermediate Value Theorem and Ensuring Continuity
The third paragraph covers the intermediate value theorem and the continuity of functions. The ninth problem applies the theorem to a function that is continuous on the interval from 0 to 2, where the function values at the endpoints are negative five and positive seven, respectively. The theorem guarantees the existence of a root within this interval, and by setting the function equal to zero, the value of c is found to be 1. The tenth problem addresses making a function continuous at x equals two by equating two different functions and solving for the value of c. After simplifying and solving the equation, c is found to be 3, ensuring the function's continuity at the given point.
Mindmap
Keywords
💡Limit
💡Direct Substitution
💡Factoring
💡Complex Fractions
💡Rational Functions
💡Trigonometric Functions
💡Horizontal Asymptote
💡Squeeze Theorem
💡Intermediate Value Theorem
💡Continuity
Highlights
The video quiz introduces methods for solving limits of functions, emphasizing the importance of understanding different techniques for various types of problems.
Direct substitution is a straightforward method for finding the limit of a function when it doesn't result in an undefined value.
When direct substitution leads to a zero in the denominator, factoring can be used to simplify the expression and find the limit.
Complex fractions can be simplified by multiplying both the numerator and denominator by the common denominator to find the limit.
The concept of rational functions and how to handle them when they involve square roots is explained, demonstrating the process of simplifying before evaluating the limit.
The video quiz addresses the challenge of evaluating limits when the function results in an indeterminate form, such as zero over zero, by checking the left and right-sided limits.
Trigonometric functions and their limits are discussed, with a focus on the behavior of the tangent function and how to simplify it using sine and cosine.
The horizontal asymptote of a function is determined using limits, highlighting the behavior of the function as the variable approaches infinity.
The squeeze theorem is introduced as a method for finding the limit of a function when the function is squeezed between two other functions with known limits.
The intermediate value theorem is explained, detailing its requirements and how it guarantees the existence of a root within a specified interval.
The process of making a function continuous at a specific point is demonstrated, showing how to find the value of a constant that achieves this goal.
The video quiz provides a comprehensive overview of various techniques for evaluating limits, showcasing the importance of adaptability and critical thinking in problem-solving.
Each problem in the video quiz is approached with a step-by-step explanation, making it easier for viewers to understand and apply the concepts.
The video quiz emphasizes the practical application of mathematical theories, such as limits and asymptotes, in solving real-world problems.
The transcript serves as a valuable resource for students and educators looking to enhance their understanding of limits and related mathematical concepts.
The video quiz's approach to teaching limits is both systematic and thorough, ensuring that viewers can confidently tackle a variety of problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: