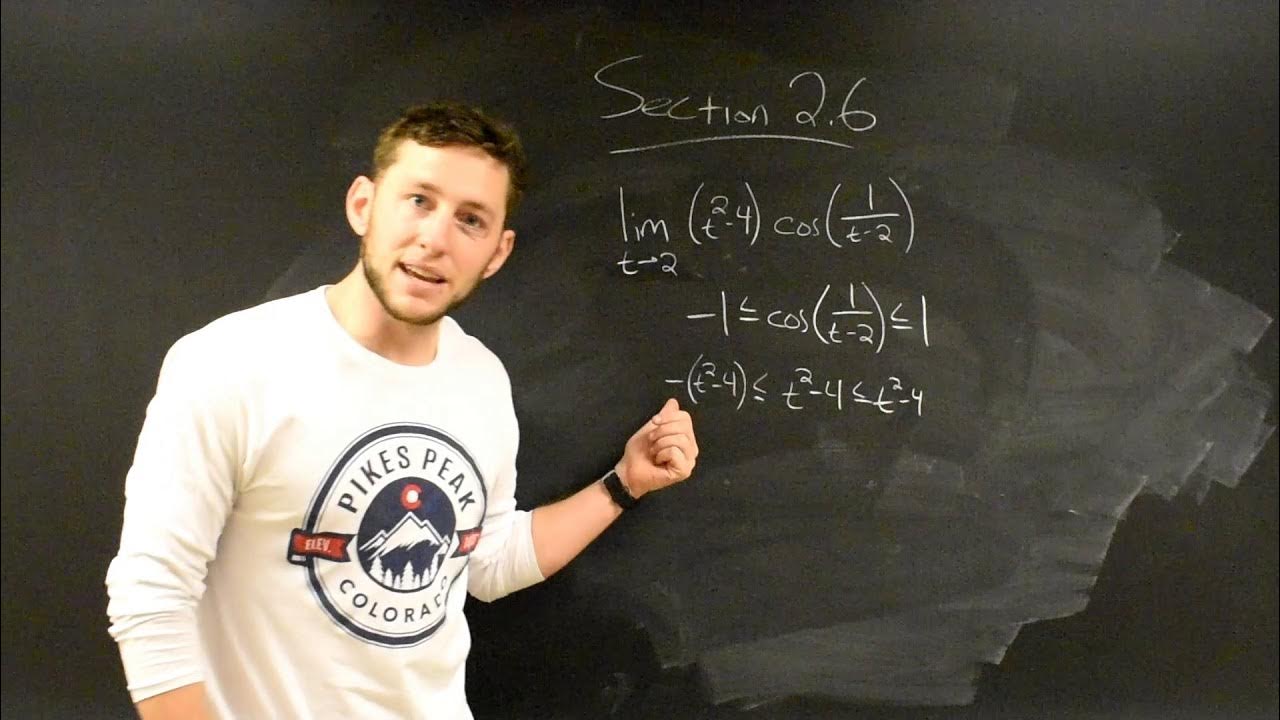Calculus Math 133 Worksheet 1
TLDRThe video script is an in-depth walkthrough of solving various limit problems in calculus. It covers a range of topics including the competition of limits, factoring techniques, and the application of the squeeze theorem. The presenter demonstrates how to approach limits by substitution, factoring, and using conjugates for square root functions. The script also discusses vertical asymptotes and how to identify them through limit analysis. Several multiple-choice questions (McQs) are addressed, with detailed solutions provided for each. The presenter concludes with essay questions, where limits are evaluated using graphical analysis and algebraic manipulation. The video is an excellent resource for learners seeking to enhance their understanding of limits and their applications in calculus.
Takeaways
- 📚 The worksheet covers solutions related to sections 2.2 and 2.3, focusing on limit computations and vertical asymptotes.
- ✅ For MCQ 1, the limit of a rational function as x approaches -5 is found by substitution, factoring, and simplification, resulting in the answer C.
- 🔍 MCQ 2 involves computing the limit of a function as T approaches 3, using the conjugate method for the square root in the denominator, leading to the answer A.
- 🚫 In MCQ 3, the vertical asymptotes of a rational function are determined by finding where the denominator equals zero, with x = 3 being the only vertical asymptote, corresponding to answer B.
- 🧮 MCQ 4 applies the squeeze theorem to evaluate the limit of a function involving cosine as x approaches 1, concluding the limit to be 0, which is answer D.
- 📈 The essay questions involve using graphs to evaluate limits, understanding continuity and discontinuity, and applying algebraic techniques to find limits and values of variables.
- 🔢 For essay question 2, the value of 'c' is determined to be 7.9 by equating the left and right limits as T approaches 2, ensuring the limit exists.
- 💡 Essay question 3 demonstrates that the value of 'K' is -5 to ensure the limit exists as X approaches 2, showcasing the use of factoring to simplify expressions.
- 📌 In essay question 4, the limit as X approaches -2 is found by ensuring the denominator does not equal zero, leading to the value of 'a' being 15 for the limit to exist.
- 📘 The final essay question uses the squeeze theorem to find the limit of a function defined by a double inequality, without explicit knowledge of the function's expression.
- ✨ The worksheet emphasizes the importance of factoring, the use of conjugates, and the squeeze theorem in calculating limits and understanding the behavior of functions.
Q & A
What is the first step in solving the limit problem for the rational function x^2 - 25 / (x^2 + 2x - 50) as x approaches -5?
-The first step is to substitute the value of x with the limit point, which is -5, to see the situation of the limit.
What is the term used to describe a limit that initially results in 0/0 after substitution?
-The term used is 'indeterminate form', which means that the limit cannot be concluded yet and further manipulation of the function is required.
How does one factor the numerator x^2 - 25 in the given limit problem?
-The numerator x^2 - 25 can be factored as (x - 5)(x + 5) because it is a difference of squares.
What is the final answer to the limit problem for the first multiple-choice question?
-The final answer to the limit problem is C, which is 5/4 after simplification.
What is the conjugate of the expression under the square root in the second limit problem, and how is it used?
-The conjugate of the expression under the square root is obtained by changing the sign between the two terms. It is used to simplify the expression and avoid the indeterminate form 0/0.
What is the conclusion for the vertical asymptote of the function f(x) = (x^2 - 5x + 6) / (x^2 - 3x + 2)?
-The only vertical asymptote is at x = 3, as the limit approaches positive or negative infinity depending on the direction of approach.
How does the Squeeze Theorem apply to the limit problem involving cosine in the range of -1 to 1?
-The Squeeze Theorem is applied by placing the function between two other functions whose limits are known as x approaches 1. Since the cosine function is bounded between -1 and 1, the limit of the function must approach 0 as x approaches 1.
What is the condition for the limit to exist as T approaches 2 in the second essay question?
-The condition for the limit to exist as T approaches 2 is that the two one-sided limits (approaching from the left and right) must be equal.
How does one find the value of K for which the limit exists as X approaches 2 in the third essay question?
-To find the value of K, one must solve the equation that results from setting the denominator to zero, which gives the vertical asymptotes. The value of K is found such that it eliminates the vertical asymptote at x = 2.
What is the method to factor the numerator of the function in the third essay question?
-The method to factor the numerator is to first find the roots of the quadratic equation, which can be done by solving the quadratic equation or by using the quadratic formula. Once the roots are found, the factored form is obtained by multiplying (x - root1)(x - root2).
What is the conclusion of the limit as X approaches 1 from the left in the fourth essay question using the Squeeze Theorem?
-The conclusion of the limit as X approaches 1 from the left is -1, which is determined by the bounds given by the functions on either side of the function f(x).
Outlines
📚 Worksheet Solutions: Limits and Rational Functions
The video script begins with an introduction to solving worksheet number one, focusing on sections 2.2 and 2.3. It addresses multiple-choice question (McQ) number one, which involves calculating the limit of a rational function as x approaches -5. The presenter uses substitution to simplify the expression and encounters an indeterminate form. To resolve this, the numerator and denominator are factored, leading to a determinate limit of 5/4. The explanation continues with McQ number two, which involves computing limits as a function of time (T) approaches 3, with a focus on square root functions.
🔍 Indeterminate Forms and Conjugates in Limit Calculations
In this paragraph, the presenter tackles an indeterminate form (0/0) that arises when computing the limit of a function as T approaches 3. The solution involves using the conjugate of the square root expression in the denominator to simplify the function. The conjugate method changes the sign between the two terms in the square root, allowing the limit to be determined as T approaches 3. The detailed process of applying the conjugate and simplifying the expression is explained, emphasizing the importance of keeping the function's form consistent during the transformation.
📐 Identifying Vertical Asymptotes through Limit Analysis
The presenter discusses the concept of vertical asymptotes and how to identify them by examining limits as x approaches specific values. The term 'vertical asymptote' is defined, and the conditions under which x = a can be considered a vertical asymptote are outlined. The focus then shifts to finding the equation of vertical asymptotes for a given rational function. Candidates for vertical asymptotes are identified by setting the denominator equal to zero and solving for x. The limits at these points are computed to confirm whether they are indeed vertical asymptotes. The process is illustrated with an example involving factoring and limit computation.
🧮 Evaluating Limits Using Factoring and Simplification
The script continues with a detailed explanation of evaluating limits by factoring and simplifying rational functions. The presenter demonstrates how to factor both the numerator and the denominator to simplify the expression before substituting the value for which the limit is being sought. The process is shown for two different limits: as x approaches 3 and as x approaches 2. The results of these computations help determine whether the points are vertical asymptotes or removable discontinuities. The presenter emphasizes the importance of verifying the factoring process to ensure accuracy.
🔢 Squeeze Theorem and Limit Evaluations
The presenter evaluates limits using the Squeeze theorem, which involves bounding a function between two others whose limits are known as x approaches a certain value. The range of the cosine function is used to establish the bounds, and the limits are computed as x approaches 1. The Squeeze theorem is then applied to show that the limit of the function must be zero. The explanation is followed by an essay question that requires evaluating limits using a graph, where the left and right limits are considered to determine the existence of a limit at a given point.
🏞️ Limit Existence and Function Continuity
The script discusses the conditions for the existence of limits as a function approaches a certain value. It explores the concept of continuity and discontinuity, emphasizing the need to compute both left and right limits to determine if a limit exists. The presenter provides a method to ensure the existence of a limit by equating the left and right limits at a point. This is illustrated with an example involving the function G of t, which is defined by two different expressions on either side of the point in question.
🧵 Factoring Quadratic Equations for Limit Computation
The presenter offers an alternative method for factoring quadratic equations when direct factoring is challenging. This involves solving the quadratic equation for its roots using the quadratic formula and then using these roots to factor the quadratic expression. The process is demonstrated with an example, showing how to find the roots and subsequently factor the expression. The factored form is then used to simplify the limit computation as the variable approaches a specific value.
🎯 Applying Squeeze Theorem with Unknown Function Bounds
The final paragraph deals with the application of the Squeeze theorem when the function's expression is unknown, but bounds are provided in the form of a double inequality. The presenter shows how to find the limit of such a function as x approaches 1 minus, using the bounds to apply the Squeeze theorem. The limits of the bounding functions are computed, and it is concluded that the limit of the function f of x as x approaches 1 minus is minus one, without needing to know the explicit form of the function.
Mindmap
Keywords
💡Limit
💡Rational Function
💡Indeterminate Form
💡Factoring
💡Conjugate
💡Vertical Asymptote
💡Squeeze Theorem
💡Continuity and Discontinuity
💡Quadratic Equation
💡Double Inequality
💡Substitution
Highlights
The transcript begins with a discussion on solving limits using substitution and factoring techniques for rational functions.
An indeterminate form of 0/0 is encountered and resolved by factoring the numerator and denominator of the function.
The concept of the squeeze theorem is introduced and applied to evaluate limits where the function is bounded between two other functions.
The use of conjugates is explained to simplify expressions involving square roots, which is crucial for determining limits in certain functions.
The procedure to find vertical asymptotes is detailed, emphasizing the importance of setting the denominator equal to zero and solving for x.
The transcript illustrates how to handle removable discontinuities by computing limits at the points of interest.
The concept of continuity and discontinuity in functions is briefly mentioned, setting the stage for further discussion in subsequent sections.
The use of graph analysis to evaluate limits is demonstrated, showing how to determine limits by approaching a point from the left and right.
The transcript provides an example of how to find the limit of a function as x approaches a specific value using algebraic manipulation.
The process of factoring quadratic expressions is shown as a method to simplify functions and find their limits more easily.
The application of the squeeze theorem to find limits without explicit knowledge of the function's expression is demonstrated.
The transcript highlights the use of linear equations to find values of variables that make the limit of a function exist.
A detailed walkthrough of solving a limit using factoring and substitution techniques is provided, emphasizing the step-by-step process.
The concept of limits at infinity is briefly touched upon when discussing vertical asymptotes and their impact on function behavior.
The transcript concludes with a summary of the methods used to evaluate limits, reinforcing the importance of factoring and the squeeze theorem.
Throughout the transcript, the importance of verifying factoring steps is emphasized to ensure the accuracy of limit calculations.
An alternative method using the solution of a quadratic equation is presented for cases where direct factoring is difficult.
The transcript ends with a comprehensive example applying the discussed concepts to find the limit of a function as it approaches a specific value.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: