Limit examples (part 2) | Limits | Differential Calculus | Khan Academy

Khan Academy
30 Sept 200706:58
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of limits in calculus, using the function f(x) = 1/x as a primary example. It explains how the value of the function changes as x approaches zero from both the positive and negative directions, highlighting the asymptotic behavior and the concept of infinity as a limit. The script also introduces the notation for one-sided limits and emphasizes the importance of limits in understanding mathematical functions.

Takeaways
  • 📈 When x approaches 0 from the negative side, the value of f(x) approaches negative infinity for the function 1/x.
  • 📊 As x gets closer to 0 from the positive side, the value of f(x) increases and approaches positive infinity for 1/x.
  • 🔄 For the function 1/x, the limit from the negative side is negative infinity, while from the positive side it is positive infinity, making the overall limit undefined.
  • 📈 For the function 1/x^2, as x approaches 0 from both the negative and positive sides, the value of the function approaches infinity.
  • 🔢 The value of 1/x^2 is always positive regardless of whether x is negative or positive, because the negative sign is negated by squaring the value of x.
  • 📊 The graph of 1/x^2 is symmetric on both sides of the y-axis and approaches infinity as x gets closer to 0 from either direction.
  • 🌐 Understanding limits is crucial in calculus as it helps in identifying behavior of functions, especially around points of discontinuity.
  • 🎓 The concept of infinity is a powerful tool in mathematics and is a legitimate answer when dealing with limits.
  • 🚀 The excitement of learning about limits and infinity can spark a deeper interest in mathematical concepts and their applications.
  • 📝 It is important to practice multiple limit problems to gain a solid understanding of the concept and its applications.
  • 📚 A formal, rigorous mathematical definition of limits will be provided in subsequent presentations, which will further solidify the understanding of this fundamental concept.
Q & A

  • What happens to the function f(x) as x approaches 0 from the negative side?

    -As x approaches 0 from the negative side, the value of f(x) becomes larger and larger negative numbers, or smaller and smaller negative values. For example, when x is -0.001, f(x) is -1,000,000.

  • What is the limit of 1/x as x approaches 0 from the positive direction?

    -The limit of 1/x as x approaches 0 from the positive direction is positive infinity.

  • What is the limit of 1/x as x approaches 0 from the negative direction?

    -The limit of 1/x as x approaches 0 from the negative direction is negative infinity.

  • Why is the limit of 1/x as x approaches 0 undefined?

    -The limit of 1/x as x approaches 0 is undefined because the value approaches different things from the positive and negative sides (positive infinity from the positive side and negative infinity from the negative side), and for a limit to be defined, these values must be equal.

  • What is the value of 1/x^2 when x is 0.1?

    -The value of 1/x^2 when x is 0.1 is 100, since 0.1 squared is 0.01 and 1 divided by 0.01 is 100.

  • Does the sign of x affect the value of 1/x^2?

    -No, the sign of x does not affect the value of 1/x^2 because squaring a number (whether positive or negative) always results in a positive value.

  • What is the limit of 1/x^2 as x approaches 0 from the negative side?

    -The limit of 1/x^2 as x approaches 0 from the negative side is positive infinity, as the value of the function increases without bound as x gets closer to 0.

  • What is the limit of 1/x^2 as x approaches 0 from the positive side?

    -The limit of 1/x^2 as x approaches 0 from the positive side is also positive infinity, for the same reason as from the negative side; the function value increases without bound.

  • What is the general limit of 1/x^2 as x approaches 0?

    -The general limit of 1/x^2 as x approaches 0 is positive infinity, as the function goes to infinity from both the positive and negative directions.

  • How does the concept of infinity as an answer in limit problems differ from other mathematical concepts?

    -Infinity as an answer in limit problems is different because it represents a value that the function approaches but never actually reaches. This is a legitimate mathematical concept that indicates the function's behavior as the input gets arbitrarily close to a certain point.

  • Why is it important to understand the behavior of functions as they approach certain values?

    -Understanding the behavior of functions as they approach certain values is crucial in calculus and mathematical analysis because it helps in predicting the long-term behavior of functions, solving equations, and gaining insights into the properties and applications of the functions.

Outlines
00:00
📈 Understanding Asymptotes and Limits: The Behavior of 1/x as x Approaches 0

This paragraph discusses the behavior of the function 1/x as it approaches 0 from both the negative and positive directions. It explains that as x gets closer to 0 from the negative side, the function values become increasingly negative, reaching negative infinity. Conversely, as x approaches 0 from the positive side, the function values increase and reach positive infinity. The speaker illustrates this with examples of function evaluations at specific points and describes the graph's behavior, noting that the limit from both sides does not equal the same value, rendering the overall limit undefined. The explanation is enriched with a visual description of the graph, emphasizing the asymptotic behavior and the concept of infinity in the context of limits.

05:01
🚀 Exploring the Limit of 1/x^2 as x Approaches 0: Infinity Emerges

The second paragraph delves into the limit of the function 1/x^2 as x approaches 0. It highlights that squaring x, whether it is positive or negative, always results in a positive value. The speaker provides examples of function evaluations at -0.1 and 0.1, demonstrating that the output is positive 100 in both cases. The graph of this function is described as symmetric, with both the negative and positive approaches to 0 leading to infinity. The speaker expresses excitement about the concept of infinity as a valid answer in the study of limits, indicating a deeper appreciation for the mathematical concepts being discussed. This paragraph emphasizes the importance of understanding how limits behave in different scenarios and the significance of infinity in those contexts.

Mindmap
Keywords
💡limit
In the context of the video, 'limit' refers to the value that a function approaches as the input (x) gets arbitrarily close to a certain point. It is a fundamental concept in calculus and mathematical analysis, used to describe the behavior of functions, especially at points where the function may not be defined or where there is a sharp change in the function's value. For example, the video discusses the limit of 1/x as x approaches 0 from the positive and negative directions, highlighting how the limit is not the same from both sides, leading to an undefined limit.
💡asymptote
An 'asymptote' is a line that a curve approaches but never actually intersects, no matter how far the curve extends. In the video, the concept is used to describe the behavior of the function 1/x as x approaches 0, where the function gets infinitely close to the x-axis (y = 0) but never actually reaches it, illustrating the vertical asymptote at x = 0.
💡infinity
The term 'infinity' represents a concept of unbounded quantity, something that is greater than any number and continues to increase without end. In the video, infinity is used to describe the limit of certain functions as their input values approach specific points. For instance, the limit of 1/x as x approaches 0 from either direction is infinity, indicating that the output values of the function become larger and larger without bound.
💡negative infinity
Negative infinity is a concept used to describe an infinitely large negative value. In the video, it is mentioned as the limit of the function 1/x as x approaches 0 from the negative side, meaning that the function values become extremely large in the negative direction without ever reaching a definite value.
💡positive infinity
Positive infinity is a concept representing an infinitely large positive value. In the video, the limit of the function 1/x as x approaches 0 from the positive side is described as positive infinity, indicating that the function values increase without bound as they get closer to zero from the right.
💡undefined
In mathematics, 'undefined' means that a particular operation or expression does not have a determined value. In the video, the limit of 1/x as x approaches 0 is said to be undefined because the function approaches different values (positive infinity and negative infinity) from the positive and negative sides of zero, which cannot be reconciled into a single value.
💡function
A 'function' is a mathematical relation that assigns a single output value to each input value. In the video, the functions 1/x and 1/x^2 are discussed, with a focus on their behavior as the input (x) approaches zero. Functions are a central concept in calculus and are used to model various relationships and processes in mathematics, science, and engineering.
💡evaluation
In mathematics, 'evaluation' refers to the process of determining the value of an expression by substituting specific values into the expression. In the video, the speaker asks the viewer to evaluate the function f(x) = 1/x at x = -0.001 to understand the behavior of the function as x approaches zero from the negative side.
💡graph
A 'graph' is a visual representation of the relationship between variables, typically used in mathematics to illustrate the behavior of functions. In the video, the speaker describes the graphs of the functions 1/x and 1/x^2 to help viewers visualize how the functions behave as they approach zero from both positive and negative directions.
💡squared
The term 'squared' refers to the mathematical operation of multiplying a number by itself. In the video, the function 1/x^2 is discussed, where squaring x results in the function always producing positive values regardless of whether x is positive or negative, as the negative sign is eliminated by squaring.
💡symmetry
In mathematics, 'symmetry' often refers to a property of a shape or function where one part is a mirror image of the other. In the video, the symmetry of the graph of 1/x^2 is mentioned, indicating that the behavior of the function as x approaches 0 from the positive side is a mirror image of its behavior from the negative side, both approaching infinity.
Highlights

The function f(x) approaches -1000 as x gets closer to 0 from the negative side.

As x approaches 0 from the negative direction, f(x) yields increasingly smaller negative numbers.

When x is 0.01, f(x) equals positive 100, demonstrating a consistent pattern of positive outcomes as x becomes more positive.

The graph of the function visually represents the behavior of the function as x approaches 0 from both the positive and negative directions.

The limit of 1/x as x approaches 0 from the positive side is positive infinity.

Similarly, the limit of 1/x as x approaches 0 from the negative side is negative infinity.

The limit of 1/x is undefined since the values from the positive and negative sides do not equal the same thing.

For the function 1/x^2, the outcome is always positive regardless of whether x is negative or positive.

Squaring x, whether it is negative or positive, results in a positive value, hence 1/x^2 is always positive.

The graph of 1/x^2 approaches infinity as x gets closer to 0 from both the negative and positive sides.

The limit of 1/x^2 as x approaches 0 from the negative side is infinity.

The limit of 1/x^2 as x approaches 0 from the positive side is also infinity.

The general limit of 1/x^2 as x approaches 0 is infinity, highlighting the legitimacy of infinity as a mathematical answer.

The concept of limits introduces a new level of understanding in mathematics, where infinity becomes a valid and exciting answer.

Further presentations will delve into more limit problems, emphasizing the importance of practice in understanding this mathematical concept.

Formal and rigorous mathematical definitions of limits will be provided in upcoming presentations.

Transcripts

Browse More Related Video

Limits at Infinity & Horizontal Asymptotes

Limits via Graphs!

Introduction to infinite limits | Limits and continuity | AP Calculus AB | Khan Academy

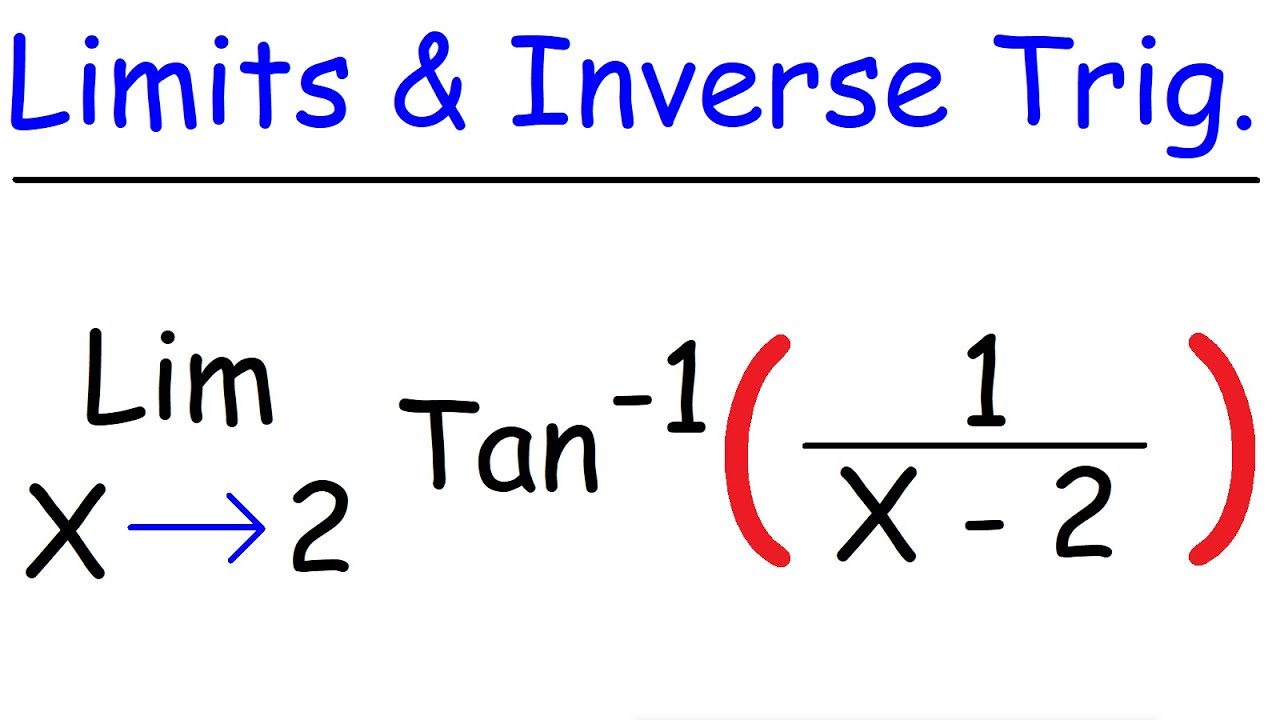
Limits of Inverse Trigonometric Functions | Calculus

A Tale of Three Functions | Intro to Limits Part II

Business Calculus - Math 1329 - Section 1.5 (and 1.6) - Limits and Continuity

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusLimitsFunctionsInfinityAsymptotesGraphingMathematicsEducationConcept ExplanationVisual Learning