Projectile Motion: Shooting a Basketball Problem
TLDRIn this engaging physics lesson, the speaker tackles a projectile motion problem involving a basketball shot. The problem is set up with the player standing 15 feet from the rim and shooting at a 45-degree angle. The speaker methodically calculates the required initial velocity for the ball to go through the hoop, determines the time it takes for the ball's trajectory, finds the maximum height reached by the ball, and finally computes the speed and angle at which the ball passes through the hoop. The solution involves using the principles of projectile motion, including the equations for horizontal and vertical displacement, and trigonometric relationships.
Takeaways
- 🏀 The problem involves projectile motion of a basketball shot from a player standing 15 feet away from the rim, with the ball initially 7 feet above the ground.
- 🎯 The basketball is launched at a 45-degree angle, but the initial velocity is unknown, which is the first question to solve.
- 🕒 The second question asks for the total time it takes for the basketball to travel its trajectory and reach the hoop.
- 📈 The third question seeks to find the maximum height reached by the basketball during its flight.
- 🏀 The final part of the problem asks for the speed and the angle of the basketball as it passes through the hoop.
- 📐 The physics ninja sets up the problem using the standard coordinate system and separates the motion into horizontal (x-direction) and vertical (y-direction) components.
- 📝 The initial velocity is calculated using the horizontal displacement (15 feet converted to meters) and the vertical displacement (3 feet converted to meters).
- 🕓 Time is determined by dividing the horizontal displacement by the horizontal component of the initial velocity.
- 🚀 The maximum height is found by setting the vertical velocity to zero at the peak of the trajectory and solving for the vertical displacement at that point.
- 📊 The speed at the hoop is calculated using the Pythagorean theorem to combine the horizontal and vertical components of the velocity.
- 🔢 The angle at which the basketball enters the rim is found using trigonometry, specifically the tangent function, based on the components of velocity at that point.
- 👍 The video encourages viewers to engage by leaving comments, subscribing to the channel, and liking the video if they found it helpful.
Q & A
What is the problem setup in the transcript?
-The problem involves a basketball player shooting a free throw. The player is 15 feet away from the rim and launches the ball at a 45-degree angle from a height of 7 feet above the ground. The goal is to find the initial velocity required for the ball to go through the basket, which is 10 feet above the ground.
How is the initial velocity calculated for projectile motion?
-The initial velocity (v_zero) is calculated by using the horizontal displacement (l) and the angle of projection (theta). The formula derived from the equations of motion is the square root of (g * l^2 / (l - h)), where g is the acceleration due to gravity and h is the vertical displacement.
What is the significance of the 45-degree angle in this problem?
-The 45-degree angle is the angle at which the basketball is launched. It is significant because it allows for the maximum range of the projectile motion, which is necessary for the ball to reach the basket.
How is the time of flight calculated for the basketball?
-The time of flight is calculated by dividing the horizontal displacement (l) by the initial horizontal velocity (v_zero * cos(theta)). This gives the time it takes for the ball to travel the 15 feet to the basket.
What is the maximum height reached by the basketball?
-The maximum height reached by the basketball is calculated by substituting the time it takes to reach the peak into the vertical motion equation. The result is one half of the square of the initial velocity times the sine squared of the angle, divided by the acceleration due to gravity (g).
How is the speed of the ball as it passes through the hoop determined?
-The speed of the ball as it passes through the hoop is determined by calculating the magnitude of the velocity vector at that point. This is done by using the horizontal and vertical components of the velocity and applying the Pythagorean theorem.
What is the angle of the ball as it passes through the hoop?
-The angle of the ball as it passes through the hoop is found by using the tangent function and the ratio of the vertical component of the velocity to the horizontal component at the time of passing through the hoop. The calculated angle is approximately 31 degrees with respect to the horizontal.
Why is it important to consider the vertical displacement in the problem?
-The vertical displacement is important because it accounts for the height difference between the player and the basket. This displacement must be accounted for in the projectile motion equations to accurately determine the required initial velocity and the time of flight.
How does the acceleration due to gravity affect the projectile motion?
-The acceleration due to gravity (g) affects the projectile motion by causing the ball to accelerate downwards. It is a key factor in the vertical motion equation and influences both the maximum height reached by the ball and the time it takes to reach the ground or the basket.
What units are used in the problem, and why are they important?
-The problem uses SI units because they provide a consistent and standardized system for calculations. The conversion from feet to meters is necessary to ensure that all measurements are in the same unit, which is crucial for accurate calculations and comparisons.
What is the role of trigonometry in solving this problem?
-Trigonometry plays a crucial role in solving this problem as it allows for the calculation of the initial velocity components, the determination of the angle of the ball as it passes through the hoop, and the simplification of the equations involving the angle of projection.
Outlines
🏀 Introduction to Projectile Motion Problem
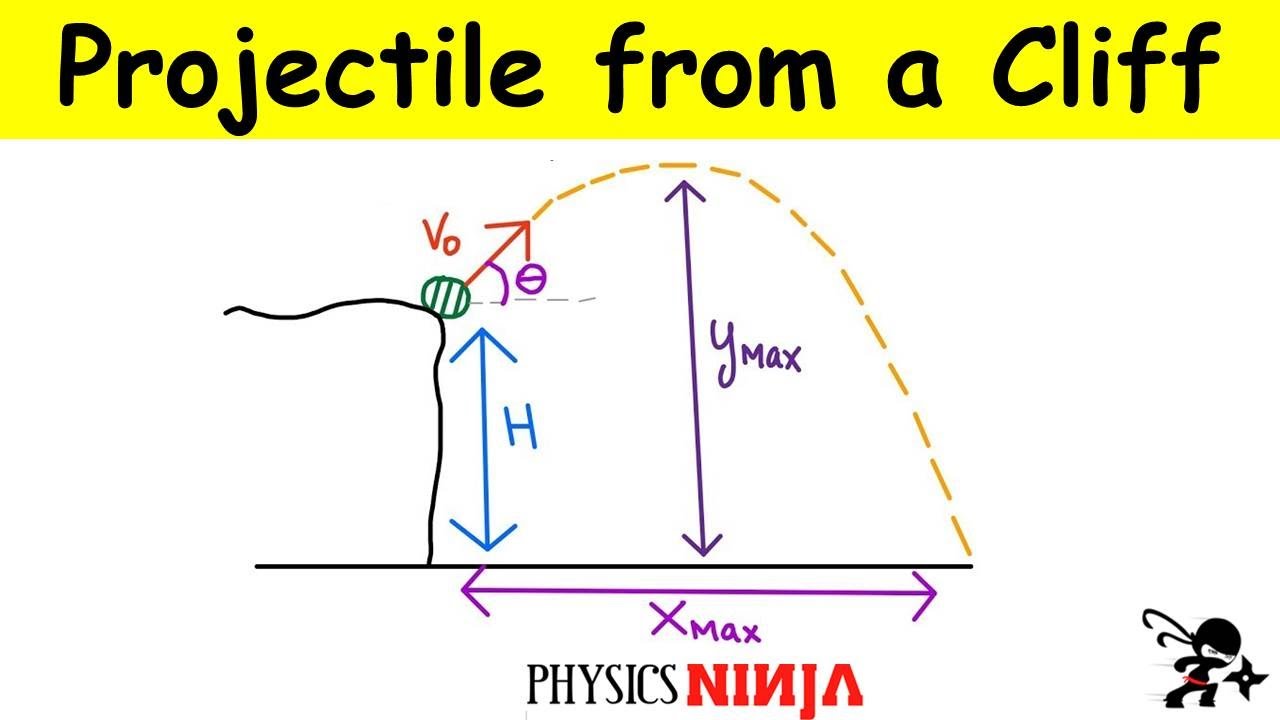
The paragraph introduces a physics problem involving projectile motion, specifically focusing on a basketball player shooting a free throw. The problem is set up with the player standing 15 feet away from the rim and launching the ball at a 45-degree angle from a height of 7 feet above the ground. The goal is to determine the initial velocity required for the ball to go through the basket, which is 10 feet above the ground. The problem is divided into four parts: calculating the initial velocity (v_zero), the time of flight, the maximum height reached by the ball, and the speed and angle of the ball as it passes through the hoop.
📐 Setting up the Equations for Projectile Motion
This paragraph delves into the process of setting up the equations necessary to solve the projectile motion problem. The speaker establishes a coordinate system and writes equations for both the horizontal (x-direction) and vertical (y-direction) motions of the basketball. The equations incorporate the initial velocity (v_naught), the angle of projection (45 degrees), and the acceleration due to gravity (g = 9.8 m/s^2). The speaker then breaks down the initial velocity into its horizontal (v_naught * cos(theta)) and vertical (v_naught * sin(theta)) components and substitutes these into the equations to simplify the process of solving for the unknowns: v_naught and time.
🧮 Solving for Initial Velocity and Time
The speaker proceeds to solve for the initial velocity (v_zero) by eliminating the time variable from the equations established in the previous paragraph. Through algebraic manipulation, the speaker isolates v_zero and calculates its value using the given horizontal displacement (l), vertical displacement (h), and the angle of projection (45 degrees). The speaker then uses the derived expression for time to calculate the time it takes for the ball to travel from the player's hands to the basket. This section provides a clear step-by-step approach to solving the first two parts of the projectile motion problem.
🔝 Determining the Maximum Height
In this paragraph, the focus shifts to finding the maximum height reached by the basketball during its trajectory. The speaker explains that at the maximum height, the vertical velocity is zero and uses this condition to calculate the time at which this occurs. The maximum height (h_max) is then found by substituting this time back into the vertical displacement equation. The speaker simplifies the equation and solves for h_max, providing the value relative to the launching point and also converting it to the height above the ground by adding the initial height of 7 feet.
🏀 Calculating Ball Speed and Entry Angle at the Rim
The final paragraph addresses the last part of the projectile motion problem, which involves calculating the speed and angle of the ball as it passes through the hoop. The speaker derives expressions for the horizontal (vx) and vertical (vy) components of the ball's velocity at the moment it enters the rim. Using the calculated components, the speaker applies the Pythagorean theorem to find the magnitude of the velocity. Additionally, the speaker uses trigonometry to determine the angle (alpha) at which the ball enters the rim, taking into account the horizontal direction and the vertical drop from the initial height. The paragraph concludes with a summary of the entire problem and its solution.
Mindmap
Keywords
💡Projectile Motion
💡Free Throw
💡Initial Velocity
💡Angle
💡Trajectory
💡Acceleration Due to Gravity
💡Horizontal Displacement
💡Vertical Displacement
💡Maximum Height
💡Speed and Angle at the Rim
💡Trigonometry
Highlights
The basketball player stands 15 feet away from the rim and launches the ball at a 45-degree angle.
The initial height of the ball above the ground is 7 feet.
The basketball hoop is 10 feet above the ground.
The goal is to calculate the required initial velocity for the ball to go through the basket.
The time taken for the ball to travel the full trajectory is a key question.
The maximum height reached by the ball during its trajectory is another problem to solve.
The speed and angle of the ball as it passes through the hoop are also to be determined.
The physics ninja uses the acceleration due to gravity as 9.8 m/s^2 in SI units.
Feet are converted to meters with 1 meter approximately equal to 3.28 feet.
The horizontal displacement (l) is 4.572 meters and the vertical displacement (h) is 0.9144 meters.
Equations for projectile motion in both x and y directions are set up and solved for the unknowns.
The initial velocity (v0) is calculated to be approximately 7.48 m/s.
The time it takes for the ball to pass through the rim is determined to be 0.864 seconds.
The maximum height achieved by the ball is calculated to be approximately 4.7 feet above the launch point.
The speed of the ball as it passes through the hoop is found to be 6.17 m/s.
The angle the ball makes as it goes through the rim is determined to be 31 degrees with respect to the horizontal.
The problem-solving approach involves simplifying the equations and substituting values to solve for the unknowns.
The use of trigonometry and algebraic manipulation is crucial in solving the projectile motion problems.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: