AP Physics Workbook 5.F Conservation of momentum in Elastic Collisions

Mr.S ClassRoom

12 May 202008:16

EducationalLearning

32 Likes 10 Comments

TLDRThis video script discusses the concept of momentum conservation, specifically focusing on a scenario where a toy car collides with a toy truck. It explains the initial and final momentum of the car and truck using a graphical representation, and how the total momentum before and after the collision remains constant. The script also introduces the concept of impulse, which is the product of force and time, and its relationship with changes in momentum. It concludes with a practical example of how to graph force versus time to determine the impulse in different collision scenarios, emphasizing the linear relationship that can be observed.

Takeaways

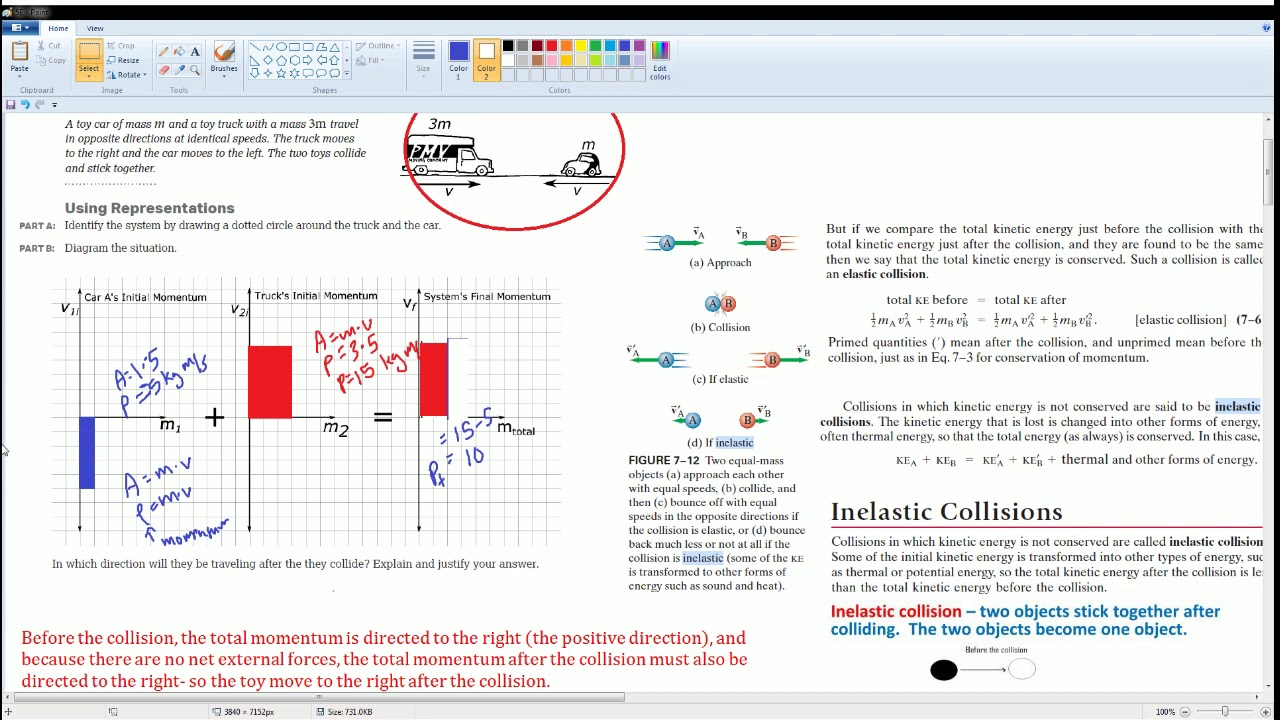
🚗 The problem scenario involves a toy car with initial velocity V colliding with a toy truck initially at rest, resulting in the car's final velocity becoming V/2.
📈 The conservation of momentum is a key principle, stating that the total initial momentum must equal the total final momentum in a closed system.
🔵 The car's initial momentum is represented as -4 times its mass (m1), and the final momentum is +2 times m1, indicating a change in direction and speed.
🚚 The truck's initial momentum is zero (since it's at rest), and its final momentum can be determined by the conservation of momentum principle.
🎨 A diagram can be used to visualize the momentum of the car, with the initial and final momentum vectors being key components.
🌟 The impulse, which is the change in momentum, is a product of the net force acting on an object and the time over which it acts (Impulse = F × Δt).
📊 When multiple trials are conducted with different surfaces (like foam, feathered clay, etc.), the change in momentum is consistent across trials.
📉 A graph of force vs. time (F vs. Δt) should yield a straight line if the change in momentum is constant, as the slope represents the impulse.
🔄 The impulse can be positive or negative, reflecting the change in the direction of momentum, and it's crucial for understanding collision effects.
📝 The final momentum of the car is the result of the impulse applied during the collision, which is a force acting over a specific time interval.

Q & A

What is the main topic of the video?
-The main topic of the video is the concept of momentum conservation in physics, specifically focusing on a scenario involving a toy car and a toy truck.
How does the toy car's initial momentum relate to its final momentum?
-The toy car's initial momentum is negative four times its mass, and its final momentum is positive two times its mass, which is half of the initial speed, in the opposite direction.
What is the initial momentum of the toy truck?
-The initial momentum of the toy truck is zero since it starts at rest.
What is the principle of momentum conservation as explained in the video?
-The principle of momentum conservation states that the total momentum of a closed system remains constant if no external forces act on it. In the video, this is demonstrated by the car and truck system where the sum of initial and final momenta must be equal.
How is the impulse related to the change in momentum?
-Impulse is the product of the net force acting on an object and the time over which it acts. It is directly related to the change in momentum, as the change in momentum (Δp) is equal to the impulse (I), which can be expressed as Δp = F * Δt.
What does the video suggest about graphing the force versus time for multiple trials of a bar dropped on different surfaces?
-The video suggests that if the momentum change is the same for each trial, graphing force (F) versus time (Δt) should result in a straight line, with the slope representing the change in momentum (impulse) and the y-intercept representing the net force.
What is the significance of the toy car's final momentum being positive?
-The toy car's final momentum being positive indicates that its direction of motion has changed; it is now moving in the opposite direction from its initial state.
How does the video demonstrate the calculation of the car's momentum at the final state?
-The video demonstrates the calculation by adding the car's initial momentum and the impulse (change in momentum) to find the final momentum, which is done by algebraic addition and subtraction, considering the direction of the velocities.
What is the role of the force sensor in the video scenario?
-The force sensor in the scenario is used to measure the average force exerted when the bar is dropped onto it from different surfaces, which is then used to analyze the change in momentum and graph the results.
How does the video use the concept of impulse to explain the interaction between the car and the truck?
-The video uses the concept of impulse to explain that the force interaction between the car and the truck results in a change in momentum for both vehicles, as the car's momentum decreases while the truck's momentum increases due to the impulse applied during the collision.
What is the practical application of understanding momentum conservation and impulse in the context of the video?
-Understanding momentum conservation and impulse is crucial in analyzing collisions and forces in real-world scenarios, such as vehicle accidents, sports impacts, and any situation where objects interact with a change in motion. The video provides a fundamental understanding of these concepts through a simple, relatable example.

Outlines

00:00

📚 Momentum Conservation in Physics

This paragraph discusses a scenario from the AP Physics workbook, focusing on the conservation of momentum, specifically section 5.5. The scenario involves a toy car being pushed towards a toy truck at a certain speed (V), then bouncing back at half the speed (V/2). The system under consideration is the car and the truck. The initial and final momenta of the car are calculated, with the initial momentum being negative (-4) and the final momentum being positive (+2). The truck's momentum change is also discussed, emphasizing the conservation of momentum principle. A diagram is sketched to illustrate the car's momentum before and after the collision, and the concept of impulse is introduced to explain the change in momentum. The paragraph concludes by showing how the algebra works to confirm the conservation of momentum.

05:00

📉 Graphing Impulse and Force

The second paragraph continues the physics theme by discussing an experiment where a bar is dropped onto a force sensor on a platform multiple times, hitting different surfaces like foam, feathered clay, etc. It explains how the momentum of the bar changes in each trial and how this change is equal to the impulse applied, which is the product of force and time (ΔP = FΔt). The paragraph then describes how to graph the results, with the change in momentum (ΔP) as the slope and the net force (F net) as the y-intercept. The linearity of the graph is attributed to the consistent change in momentum across trials. The paragraph concludes by reinforcing the concept that impulse, a force applied over time, results in a change in momentum.

Mindmap

Keywords

💡Momentum

Momentum is a fundamental concept in physics that represents the quantity of motion of an object, given by the product of the object's mass and velocity. In the video, the calculation and conservation of momentum are central to understanding the interactions between the toy car and truck during the collision. The initial and final momentum values are used to illustrate the changes in the system and to solve for unknown quantities.

💡Conservation of Momentum

The principle of conservation of momentum states that the total momentum of a closed system remains constant if no external forces act upon it. This law is crucial in the video as it allows the analysis of the collision between the car and the truck. By sketching the initial and final momentum values and ensuring their areas are equal, the conservation law helps to determine the changes in velocity and direction after the collision.

💡Impulse

Impulse is the change in momentum of an object when a force is applied over a period of time. It is a key concept in understanding how forces cause changes in motion. In the video, the impulse is calculated as the product of the force exerted during the collision and the time over which the force is applied. The impulse is used to find the force that the car experiences during the collision with the truck.

💡Collision

A collision is an event in which two or more objects interact with each other with forces that cannot be ignored, often resulting in a change of motion. In the video, the collision between the toy car and the truck is the central event that leads to the application of the conservation of momentum and impulse principles to analyze the outcome.

💡Velocity

Velocity is a vector quantity that describes the rate of change of an object's position with respect to time, and it has both magnitude and direction. In the context of the video, the initial and final velocities of the car and truck are critical in determining their momenta and the effects of the collision.

💡Force

Force is any action that, when unopposed, will change the motion of an object. It is a vector quantity that has both magnitude and direction. In the video, the force exerted during the collision is what causes the change in momentum of the car and the truck.

💡Mass

Mass is a measure of the amount of matter in an object, and it is an intrinsic property that is independent of the object's location, shape, or state. In the video, the masses of the car and the truck are essential in calculating their momenta and analyzing the collision effects.

💡Net Force

Net force is the vector sum of all the individual forces acting on an object. It is the force that results in an acceleration of the object according to Newton's second law of motion. In the video, the net force during the collision is what causes the change in momentum of the car and the truck.

💡Graph

A graph is a visual representation of data or mathematical functions, which can help in understanding patterns and relationships between variables. In the video, the concept of graphing is used to illustrate how the force and time (Δt) relationship can be represented to find the change in momentum (ΔP).

💡Worked Example

A worked example is a problem that is solved step by step, showing the process and calculations needed to reach the final answer. In the video, the scenario of the toy car and truck collision is a worked example that demonstrates the application of the principles of momentum and impulse.

💡Physics

Physics is the natural science that studies matter, its motion, and the forces that act on it. The video is an educational resource for learning about the principles of physics, specifically focusing on the concepts of momentum, impulse, and collision.

Highlights

The scenario involves a toy car and a toy truck, focusing on the conservation of momentum.

The toy car initially moves towards the toy truck at a speed V and then bounces back at half the speed.

The system considered includes both the car and the truck, emphasizing the conservation of momentum within the system.

The initial momentum of the car is negative four times its mass, and the final momentum is positive two times its mass.

The truck's initial momentum is zero, as it is at rest, and its final momentum is determined by the conservation of momentum principle.

A graphical representation of the car's momentum is provided, with the initial and final momenta depicted on a diagram.

The impulse experienced by the car is calculated by considering the change in momentum and the forces involved.

The conservation of momentum is further illustrated by comparing the total areas representing the initial and final momenta.

A separate diagram is provided for the car's momentum during the collision, showing the initial and final states.

The impulse-momentum theorem is applied, relating the change in momentum (impulse) to the force exerted over a period of time.

A method to graph the force and time relationship for a bar dropped on a force sensor is discussed, aiming for a straight line representation.

The graph should display force on the y-axis and time (Delta T) on the x-axis to exhibit the linear relationship.

The slope of the graph represents the change in momentum, which is also equivalent to the impulse.

The impulse is the product of the force and the time over which it is applied, resulting in a change in the car's momentum.

The final momentum of the car is the sum of its initial momentum and the impulse experienced during the collision.

The algebraic manipulation of the momentum values confirms the conservation of momentum principle.

The practical application of the concepts is demonstrated through the use of a force sensor and the calculation of force based on the impulse.

Transcripts

Browse More Related Video

High School Physics - Impulse-Momentum Theorem

AP Physics Workbook 5.E Conservation of momentum in Inelastic Collisions

AP Physics Workbook 5.C Impulse

2022 Live Review 5 | AP Physics 1 | Understanding Impulse and Momentum

Momentum | Forces & Motion | Physics | FuseSchool

2021 AP Physics 1 Free Response #3 (First Administration)

AP Physics Workbook 5.F Conservation of momentum in Elastic Collisions

Takeaways

Q & A

What is the main topic of the video?

How does the toy car's initial momentum relate to its final momentum?

What is the initial momentum of the toy truck?

What is the principle of momentum conservation as explained in the video?

How is the impulse related to the change in momentum?

What does the video suggest about graphing the force versus time for multiple trials of a bar dropped on different surfaces?

What is the significance of the toy car's final momentum being positive?

How does the video demonstrate the calculation of the car's momentum at the final state?

What is the role of the force sensor in the video scenario?

How does the video use the concept of impulse to explain the interaction between the car and the truck?

What is the practical application of understanding momentum conservation and impulse in the context of the video?