10 Calculator Tricks YOU NEED Before your Maths Exam | Save your Grades (AQA, Edexcel, OCR)

Brainstorm - Maths and Science
23 May 202308:32
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers 10 essential calculator tips for students preparing for their GCSE maths exam. It covers prime factorization, table functions for graphing, standard form conversions, fraction simplification, mixed number and improper fraction conversions, time conversion, digit separators for readability, ratio conversions, editing long expressions efficiently, and storing and recalling numbers for later use. These tips aim to maximize the use of calculator functions to simplify complex problems and improve exam performance.

Takeaways
  • ๐Ÿงฎ Use your calculator to find the product of prime factors of any number by using the 'fact' function after typing the number and pressing equals.
  • ๐Ÿ“Š Utilize the table function to graph equations by entering the equation, setting the 'start', 'end', and 'step' values, and the calculator will display the corresponding 'f(x)' values.
  • ๐Ÿ”ข Convert numbers into standard form and vice versa using the 'times 10x' button and the 'Eng' button, which simplifies large or scientific notation numbers.
  • ๐Ÿ“ˆ Simplify fractions and convert mixed numbers to improper fractions using the calculator's fraction functions, simplifying calculations and reducing complexity.
  • โฐ Easily convert decimal hours to hours, minutes, and seconds using a specific function on the calculator, simplifying time-related calculations.
  • ๐Ÿ” Adjust the display settings of your calculator to include a digit separator for large numbers, making them more readable and easier to interpret.
  • โš–๏ธ Convert ratios in various forms, such as 1 to n, using the calculator's ratio function, which can simplify solving ratio problems.
  • ๐Ÿ“ Edit long expressions without deleting and rewriting the entire line by using the fraction button in conjunction with brackets to insert fractions where needed.
  • ๐Ÿ’ก Store numbers in your calculator's memory for later use during calculations by using the 'sto' or 'store' button, saving time and space.
  • ๐Ÿงน Clear the calculator's memory history before an exam to ensure noไฝœๅผŠ (cheating) can occur, by using the 'shift' + 'reset' function and confirming with 'yes'.
  • ๐Ÿ€ These calculator tips are designed to help you use your calculator effectively during your GCSE math exam, potentially improving your performance and confidence.
Q & A

  • How can you find the product of prime factors of a number using a calculator?

    -To find the product of prime factors of a number, type the number into the calculator, press equals, then press the 'fact' button, which is usually accessed by holding down the shift key and pressing the button designated for factorials.

  • What is the process for using a calculator to graph a linear equation?

    -To graph a linear equation, go to the 'table' function on your calculator by pressing the menu button, selecting the table function, and entering the equation (e.g., 2x - 3). After inputting the equation, set the 'start', 'end', and 'step' values to iterate through the desired range of x-values. The calculator will then display the corresponding y-values (f(x)), which you can plot to create the graph.

  • How can you convert a decimal number into standard form using a calculator?

    -To convert a decimal number into standard form, type the number, press the 'times 10x' button the appropriate number of times to match the decimal place, and then press equals. For negative powers, use the 'Eng' button after typing the number and pressing equals.

  • What is the function of the 'Eng' button on a calculator?

    -The 'Eng' button stands for 'Engineering' mode. It is used to convert large numbers into a more manageable format by expressing them in terms of 'times 10 to the power of'. For example, pressing the 'Eng' button after entering 6,500,000 will display 6.5 times 10 to the 6.

  • How can a calculator simplify a fraction?

    -To simplify a fraction using a calculator, type the fraction, press equals, and the calculator will provide the simplified form. For example, entering 90/160 and pressing equals will yield 9/16.

  • How do you convert a mixed number to an improper fraction on a calculator?

    -To convert a mixed number to an improper fraction, enter the whole number part, press the 'shift' key and the 'S to D' (shift to divide) button, then enter the fractional part. For example, entering 54 and pressing 'shift' and 'S to D' followed by 5/7 will result in 47/7 as an improper fraction.

  • What is the purpose of the time conversion button on a calculator?

    -The time conversion button on a calculator is used to convert decimal hours into hours, minutes, and seconds. For instance, entering 6.55 and pressing the time conversion button will display the time as 6 hours and 33 minutes.

  • How can you make numbers easier to read on a calculator?

    -To make numbers easier to read, you can enable the digit separator feature on your calculator by going to 'shift' and 'menu', navigating to 'setup', and selecting the 'number one' option for digit separator.

  • How do you convert ratios in the form of 1 to n using a calculator?

    -To convert a ratio in the form of 1 to n, go to the 'menu', select the 'ratio' function, and press the button corresponding to the '1 to n' option (usually button number 2). Then, input the ratio (e.g., 90 to 40), and the calculator will provide the simplified form (e.g., 4 to 9).

  • What is a useful calculator trick for editing long expressions?

    -If you need to insert a fraction into a long expression, you can use the fraction button after typing the part of the expression that precedes the fraction. This will only capture that part, allowing you to insert the fraction without having to retype the entire expression.

  • How do you store and recall numbers in a calculator for later use?

    -To store a number, press the 'sto' (store) button, usually found above the number 7 on the calculator, and then press a letter key to save the number under that letter. To recall the number, press the 'Alpha' version of the same letter. Before an exam, ensure you clear the memory by pressing 'shift', 'reset', selecting 'memory', pressing 2 for clearing memory, and confirming with 'yes'.

Outlines
00:00
๐Ÿ“š Prime Factorization and Calculator Functions

This paragraph introduces the use of calculators for finding the product of prime factors of a number, utilizing the 'fact' function. It explains how to input a number, press 'equals', and then use the 'shift' plus a specific button to find the prime factors. The example given is 550, which factors into 2 times 5 squared times 11. Additionally, the paragraph covers using the 'table' function to graph equations like 2x - 3, inputting values for 'start', 'end', and 'step', and obtaining corresponding f(x) values. It also touches on converting between standard form and normal numbers, simplifying fractions, and converting mixed numbers to improper fractions and vice versa.

05:00
๐Ÿ“ˆ Graphing Equations and Storing Numbers

The second paragraph discusses advanced calculator functions such as graphing equations, converting ratios, handling long expressions, and storing numbers. It explains how to use the 'menu' button to access the 'table' function for graphing, setting parameters for 'start', 'end', and 'step' to generate a series of values for the function f(x). The paragraph also covers converting ratios in the form of 1 to n, simplifying long expressions by inserting fractions without retyping the entire expression, and storing numbers using the 'sto' button for easy recall during calculations. The importance of clearing the calculator's memory before an exam is also highlighted to maintain academic integrity.

Mindmap
Keywords
๐Ÿ’กPrime Factors
Prime factors are the prime numbers that divide a given number exactly, without leaving a remainder. In the context of the video, the process of finding the product of prime factors for a number like 550 is demonstrated, which involves breaking it down into 2 times 5 squared times 11. This is a fundamental skill for students preparing for their GCSE maths exam, as it helps in understanding the properties and structure of numbers.
๐Ÿ’กTable Function
The table function on a calculator is a feature that allows users to calculate and display values of a function for a range of inputs. In the video, the table function is used to calculate the values of the function f(x) = 2x - 3 for x values ranging from -2 to 2 in increments of 1. This helps in understanding the behavior of functions and can be particularly useful for graphing and analyzing linear equations.
๐Ÿ’กStandard Form
Standard form is a way of expressing numbers as a product of a number between 1 and 10 and a power of 10. For example, 3.26 can be written in standard form as 3.26 ร— 10^0. This format is useful for simplifying the representation of very large or very small numbers and is a common requirement in scientific notation. The video explains how to convert both normal numbers into standard form and vice versa, which is an essential skill for students dealing with scientific calculations.
๐Ÿ’กSimplifying Fractions
Simplifying fractions involves reducing a fraction to its simplest form, where the numerator and the denominator have no common factors other than 1. This process makes calculations easier and is a fundamental skill in arithmetic and algebra. In the video, the calculator is shown to be a useful tool for simplifying fractions like 90/160 to 9/16, which saves time and effort during calculations.
๐Ÿ’กConverting Mixed Numbers
Mixed numbers are numbers that contain both a whole number and a fraction. Converting mixed numbers to improper fractions involves multiplying the whole number by the denominator of the fraction and then adding the numerator to get a new fraction that is greater than or equal to 1. The video explains how to use the calculator to convert mixed numbers like 5 4/5 to improper fractions, which is a valuable skill for students learning to work with fractions.
๐Ÿ’กTime Conversion
Time conversion refers to the process of converting decimal hours into a more readable format such as hours, minutes, and seconds. This is particularly useful in problems involving speed, distance, and time, where time is often given in decimal form. The video demonstrates how to use the calculator to convert 6.55 hours into 6 hours and 33 minutes, making it easier to interpret and work with in calculations.
๐Ÿ’กDigit Separator
A digit separator is a symbol or character used to separate groups of digits in large numbers for easier readability. In many calculators and number formatting systems, the comma (,) is often used as a digit separator. The video explains how to enable the digit separator feature on a calculator, which helps in making large numbers like 4.5 million more readable by spacing out the digits (e.g., 4,500,000).
๐Ÿ’กRatio Conversion
Ratio conversion refers to the process of transforming a given ratio into different forms, such as 1 to n or n to 1. This is useful for understanding and solving problems that involve proportions and rates. The video demonstrates how to use the calculator's ratio function to convert a ratio like 90 to 40 into the form of 1 to n, where n is the value that makes the ratio equivalent (in this case, 4 to 9).
๐Ÿ’กExpression Simplification
Expression simplification is the process of making a mathematical expression more straightforward by reducing or eliminating complex parts. This can involve simplifying within parentheses or handling fractions within an expression. The video explains a technique for simplifying expressions without having to rewrite the entire expression, such as when a fraction needs to be added to an existing expression involving square roots.
๐Ÿ’กStoring Numbers
Storing numbers on a calculator refers to saving calculated values for later use. This can be particularly helpful when dealing with long calculations or when the same value is needed multiple times throughout a problem. The video demonstrates how to use the calculator's storage function to save a complex calculation like the cube root of 65 multiplied by the tangent of 60, and then recall the stored value later in the calculation process.
๐Ÿ’กClearing History
Clearing history on a calculator involves removing all stored values and previous calculations to ensure there is no carryover of data from one problem to another. This is an important step before starting a new set of calculations or before an exam to ensure that no unintentional data is used. The video emphasizes the importance of clearing the calculator's memory before an exam to maintain the integrity of the testing environment.
Highlights

Using a calculator to find the product of prime factors of a number, e.g., 550 = 2 * 5^2 * 11.

Accessing the 'fact' button on a calculator to compute prime factors, typically by pressing shift and a specific button.

Utilizing the table function on a calculator to compute values for a given equation, such as f(x) = 2x - 3.

Entering the equation and range (start, end, step) in the table function to generate a series of values and corresponding y-coordinates for graphing.

Converting numbers between standard form and normal numbers using calculator functions, such as 3.26 * 10^9.

Adjusting standard form values in multiples of three (e.g., 10^3, 10^6) for precise scientific notation.

Simplifying fractions using calculator functions, for example, 90/160 simplifies to 9/16.

Converting mixed numbers to improper fractions and vice versa with calculator buttons like S to D (Shift + D).

Transforming decimal hours into hours, minutes, and seconds for easier interpretation and calculation.

Activating digit separators on a calculator to enhance readability of large numbers.

Converting ratios from one form to another, such as 90:40 to 1:x and finding the value of x.

Editing long expressions on a calculator by inserting fractions without deleting and rewriting the entire expression.

Storing numbers in a calculator's memory for later use during calculations, using the 'sto' or store button.

Recalling stored values in a calculator using the 'recall' function for efficient problem-solving.

Clearing calculator memory history before an exam to ensure academic integrity.

Top 10 calculator tips for effective use in GCSE maths exams, aiming to enhance students' performance.

Transcripts

Browse More Related Video

5 Essential GCSE Maths Calculator Skills You Need To Know! | Casio Calculator

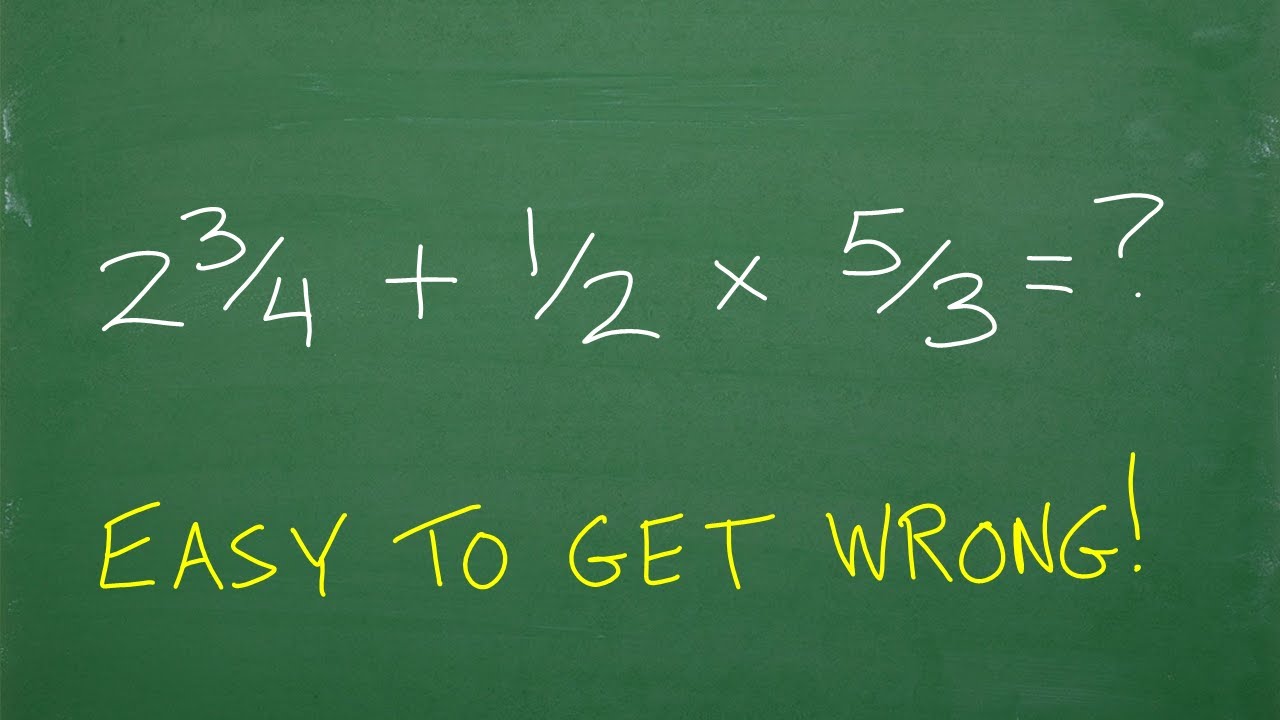
(2 and 3/4) plus 1/2 times 5/3 = ? Whatโ€™s the first thing you should be thinking in this problem?

TI-84 Plus Calculator Basic Features - Lesson 1

Ti-84 Calculator: Downloading Programs

Casio FX-991ES Plus and FX-115ES Plus 2nd Edition, Learn All Features

Calculator Techniques FOR BOARD EXAM - Evaluating Functions and Simplifying Expressions 10 EXAMPLES

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
GCSE MathsCalculator TipsPrime FactorizationGraphing FunctionsStandard FormFractions & DecimalsMixed NumbersTime ConversionRatios & ProportionsExpression SimplificationMemory Functions