How to Find the Standard Deviation, Variance, and Mean of a Sample and a Population - Easy Tutorial

PreMath
28 Oct 202011:06
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial effectively explains the process of calculating the mean, variance, and standard deviation for both a population and a sample dataset. It begins by defining the mean and demonstrates its calculation using the provided data set, resulting in a mean of 32 for both the sample and population. The video then illustrates the computation of population variance, using the data to find a value of 34.8. Following this, the sample variance is calculated, yielding a result of 43.5. Finally, the tutorial computes the population and sample standard deviations, with the population's being 5.9 and the sample's 6.6. The step-by-step breakdown is clear and informative, making it easy for viewers to understand these statistical concepts.

Takeaways
  • 📊 The mean (average) is calculated by summing all data values and dividing by the total number of values.
  • 📈 Both the sample mean (x̄) and population mean (μ) are found using the same formula, and in this case, they both equal 32.
  • 📝 Variance is a measure of how much the data deviates from the mean, and the population variance (σ²) is calculated using the formula Σ(x - μ)² divided by the population size (N).
  • 🔢 For the given dataset, the calculated population variance (σ²) is 34.8.
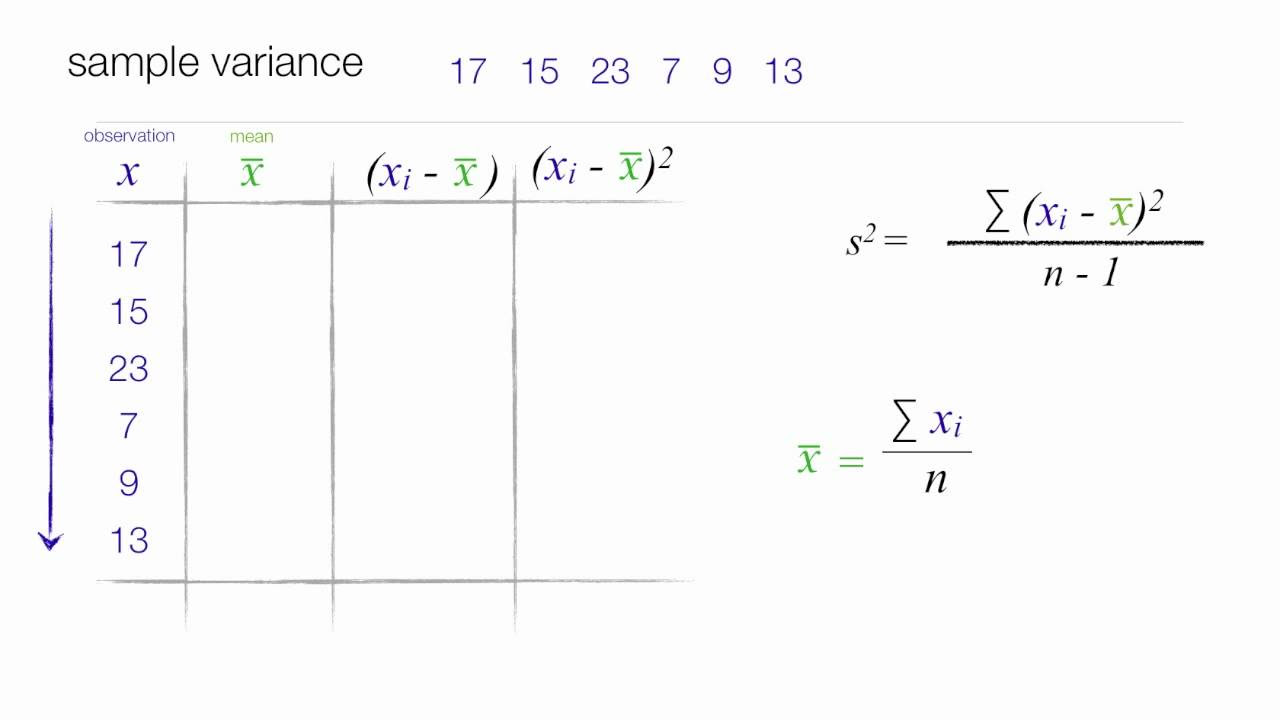
  • 🌟 The sample variance (s²) differs from the population variance by using (n-1) in the denominator, which accounts for the smaller sample size and yields a more accurate estimate for the population variance.
  • 🔄 The sample variance in this case is calculated as 174 divided by 4, resulting in 43.5.
  • 📉 Standard deviation is the square root of variance and provides a measure of dispersion in the same units as the data.
  • 🌐 The population standard deviation (σ) is found by taking the square root of the population variance (σ²), which is 5.9 for the given data.
  • 📐 Similarly, the sample standard deviation (s) is the square root of the sample variance (s²), resulting in 6.6.
  • 📋 The process of calculating mean, variance, and standard deviation is essential for understanding data distribution and making statistical inferences.
  • 🎓 Understanding these statistical concepts is crucial for analyzing data in various fields, including science, business, and social sciences.
Q & A

  • What is the main formula used to calculate the mean?

    -The main formula for calculating the mean is the sum of all data values divided by the total number of values.

  • How is the sample mean represented in the script?

    -In the script, the sample mean is represented by the symbol x bar.

  • What is the relationship between the sample mean and the population mean in the given data set?

    -In the given data set, both the sample mean and the population mean are the same, which is 32.

  • How is the population variance calculated?

    -The population variance is calculated by summing the squares of the differences between each data value and the mean (x - x bar) and then dividing by the population size (n).

  • What is the sample variance formula?

    -The sample variance formula is s square equals to the sum of the squares of the differences between each data value and the mean (x - x bar) divided by the sample size minus 1 (n - 1).

  • How does the population standard deviation relate to the population variance?

    -The population standard deviation is the square root of the population variance.

  • What is the difference between the sample variance and the population variance in terms of the divisor?

    -The sample variance is calculated using the sample size minus 1 (n - 1) as the divisor, while the population variance uses the total population size (n) as the divisor.

  • How is the sample standard deviation represented in the script?

    -In the script, the sample standard deviation is represented by the symbol s.

  • What is the purpose of calculating standard deviation?

    -The purpose of calculating standard deviation is to measure the amount of variation or dispersion in a set of values.

  • What is the significance of the sigma notation (∑) used in the script?

    -The sigma notation (∑) is used to represent the sum or addition of a series of terms, in this case, the squared differences between each data value and the mean.

  • How does the script demonstrate the calculation of the population variance and standard deviation?

    -The script demonstrates the calculation of the population variance and standard deviation by first calculating the sum of the squared differences from the mean, then dividing by the population size for variance, and finally taking the square root of the variance to obtain the standard deviation.

  • What is the final calculated value for the sample standard deviation in the script?

    -The final calculated value for the sample standard deviation in the script is 6.6.

Outlines
00:00
📊 Introduction to Finding Mean, Variance, and Standard Deviation

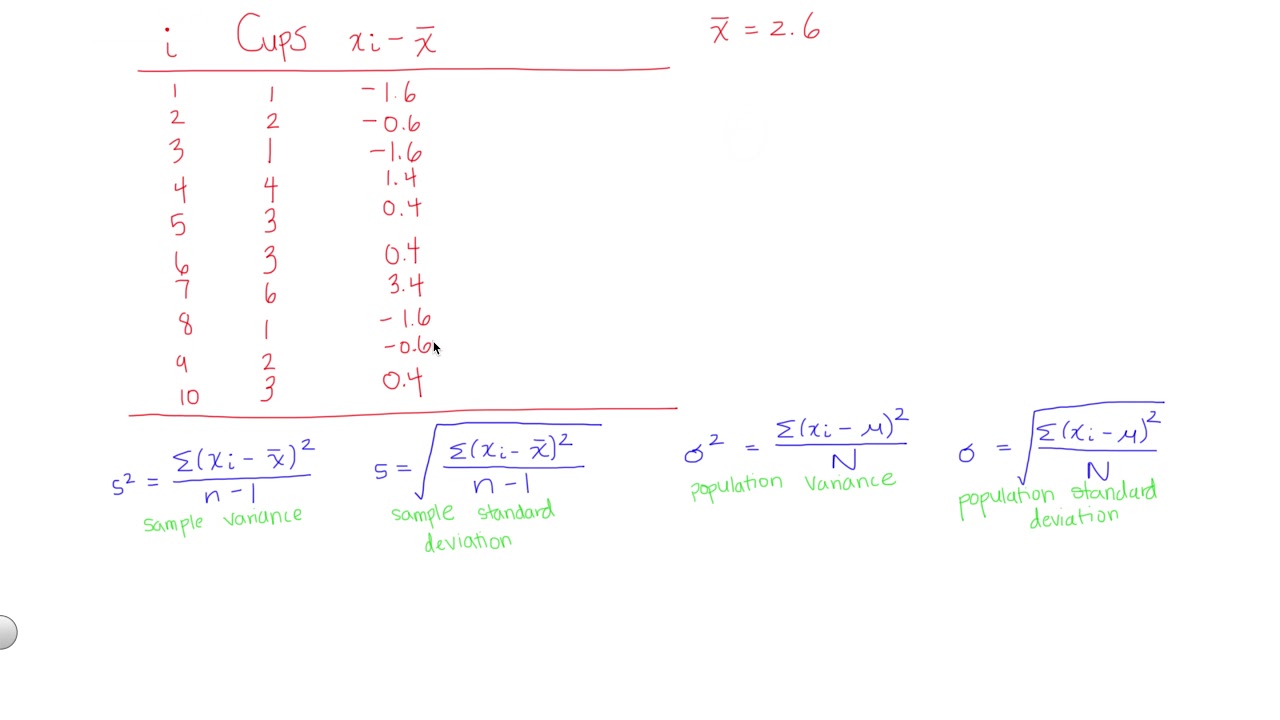
This paragraph introduces the topic of calculating the mean, variance, and standard deviation for a given data set in the context of both a population and a sample. It outlines the process of finding the mean by summing all data values and dividing by the total number of values, resulting in a sample mean of 32 and a population mean of 32, highlighting that the sample mean is denoted by x̄ and the population mean by μ. The paragraph emphasizes the importance of understanding these concepts and their applications in statistical analysis.

05:01
📈 Calculating Population Variance

The second paragraph delves into the calculation of population variance. It explains that the population variance is represented by the Greek letter sigma (σ²) and is calculated by summing the squares of the differences between each data value (x) and the population mean (μ). The paragraph provides a detailed step-by-step process, including the sigma notation for summation, and concludes with the population variance being 34.8 after dividing the sum of squared differences (174) by the population size (5).

10:04
📊 Determining Sample Variance

This paragraph focuses on the calculation of sample variance, which is a measure of variability within a sample of data. The process involves using the sum of squared differences between each data value (x) and the sample mean (x̄), divided by the sample size minus one (n-1). The paragraph explains that the sample variance, represented by s², is calculated by dividing the sum of squared differences (174) by the sample size (5) minus one, resulting in a sample variance of 43.5.

🌟 Computing Population and Sample Standard Deviation

The final paragraph discusses the computation of both population and sample standard deviations, which are measures of dispersion or spread in a set of values. The population standard deviation is found by taking the square root of the population variance (34.8), resulting in a value of 5.9. Similarly, the sample standard deviation is derived by taking the square root of the sample variance (43.5), yielding a value of 6.6. The paragraph concludes by summarizing the results and encouraging viewers to engage with more educational content on the topic.

Mindmap
Keywords
💡Standard Deviation
Standard Deviation is a measure of the amount of variation or dispersion in a set of values. In the context of the video, it is used to quantify the spread of the data points in the given dataset. The script explains how to calculate the population and sample standard deviation, with the population standard deviation being the square root of the population variance (5.9 in the example), and the sample standard deviation being the square root of the sample variance (6.6 in the example).
💡Variance
Variance measures the spread of data points around the mean. It is the average of the squared differences from the mean. In the video, the calculation of population variance and sample variance is demonstrated, with the population variance being the sum of squared differences divided by the population size (34.8 in the example), and the sample variance being the sum of squared differences divided by the sample size minus one (43.5 in the example).
💡Mean
The Mean, often referred to as the average, is a measure of central tendency that calculates the arithmetic sum of a dataset divided by the number of values in the dataset. In the video, the mean is calculated for both the population and the sample, and it is found to be 32 for both, as they are based on the same set of data points.
💡Population
In statistics, a Population refers to the entire set of items or individuals about which data is being collected. The video discusses calculating the population mean and population variance, which are based on the entire dataset without any sampling.
💡Sample
A sample is a subset of the population that is used to represent and analyze the entire population. In the video, the same dataset is also considered as a sample from a larger population, and the sample mean and sample variance are calculated to estimate the population parameters.
💡Sigma Notation
Sigma Notation, represented by the Greek letter sigma (Σ), is a mathematical symbol used to denote the sum of a series of terms. In the context of the video, sigma notation is used to represent the sum of squared differences between each data point and the mean when calculating variance and standard deviation.
💡x-bar
x-bar (pronounced 'x-bar') represents the sample mean in statistics. It is the average of the sample data and is used to estimate the population mean. In the video, x-bar is calculated and used to find the sample mean, which is 32 for the given dataset.
💡mu
Mu (μ) is the Greek letter used to represent the population mean in statistical studies. It is the average of the entire population and serves as a benchmark for comparing sample statistics. In the video, mu is used to denote the population mean, which is also found to be 32 for the given dataset.
💡Sample Size
Sample Size refers to the number of observations or individuals in a sample. It is an important factor in statistical analysis as it affects the precision of estimates and the validity of statistical tests. In the video, the sample size is used to calculate the sample variance and sample standard deviation, with the sample size being 5 for the given dataset.
💡Population Size
Population Size is the total number of individuals or observations in the entire population. It is crucial for calculating population parameters like the population mean and population variance. In the video, the population size is used in the calculation of the population variance, with the population size being equal to the number of values in the dataset, which is 5.
💡Data Points
Data Points are individual values or observations in a dataset. They represent the actual numbers that are collected and analyzed in statistical studies. In the video, the data points are the values 25, 26, 32, 37, and 40, which are used to calculate the mean, variance, and standard deviation for both the population and the sample.
Highlights

The tutorial begins with an introduction to finding the standard deviation, variance, and mean for a given data set.

Two scenarios are discussed: one for a population and another for a sample.

The mean is calculated using the formula: sum of all data values divided by the total number of values.

For the given data set, both the sample mean and population mean are found to be 32.

The sample mean is represented by x̄ (x bar), and the population mean by μ (mu).

The process for calculating the population variance is explained, emphasizing the use of the mean.

The population variance is calculated by summing the squared differences from the mean and dividing by the population size.

The calculated population variance for the given data set is 34.8.

The sample variance is calculated using a similar method but with a key difference in the denominator.

The sample variance is found by dividing the sum of squared differences by the sample size minus one.

The calculated sample variance for the given data set is 43.5.

The population standard deviation is the square root of the population variance.

The calculated population standard deviation is 5.9.

The sample standard deviation is also the square root of variance but of the sample variance.

The calculated sample standard deviation for the given data set is 6.6.

The video provides a clear and step-by-step guide to statistical calculations, suitable for educational purposes.

The tutorial concludes by encouraging viewers to subscribe for more informative content.

Transcripts

Browse More Related Video

How to calculate Standard Deviation and Variance

Variance and Standard Deviation: Why divide by n-1?

Measures of Dispersion (Ungrouped Data) | Basic Statistics

Variance - Clearly Explained (How To Calculate Variance)

How to Calculate Standard Deviation and Variance by Hand

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Premath ConceptsStatistical MeasuresMean CalculationVariance ExplanationStandard DeviationData AnalysisMathematics EducationTutorial VideoEducational ContentStatistical Learning