How convolutional neural networks work, in depth

Brandon Rohrer

17 Oct 201861:28

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the intricacies of Convolutional Neural Networks (CNNs), a key component in the field of artificial intelligence. It illustrates how CNNs process and recognize patterns in images, starting from basic line segments to complex forms like faces or car elements. The script walks through the fundamental concepts of filtering, pooling, and normalization in CNNs. It also explains how these networks learn through backpropagation and optimization, adjusting weights and features to improve accuracy. The significance of hyperparameters in shaping network architecture is highlighted. The video concludes by discussing the applicability of CNNs in various data types, emphasizing that they excel in pattern recognition within spatially organized data.

Takeaways

👨‍💻 Convolutional Neural Networks (CNNs) are pivotal in the field of AI, particularly for image recognition, transforming images into patterns and structures at various layers.
💡 CNNs can be combined with reinforcement learning for advanced applications like game playing and robot control.
📈 The initial layers of a CNN might identify simple patterns like lines, which are then built upon in deeper layers to recognize complex objects like faces or car elements.
🔧 A key technique used by CNNs is filtering, or convolution, where features of an image are matched and layered to identify patterns, employing a mathematical process that integrates pixel comparisons.
📌 Pooling, specifically max pooling, is another critical process that reduces the size of the representation, enhances feature detection, and reduces computation.
⚡ Rectified Linear Units (ReLUs) help in normalization by adjusting negative values to zero, which stabilizes the numerical computations throughout the network.
📊 CNN layers can be stacked and configured in various combinations to form highly effective architectures for specific tasks.
📆 Backpropagation and gradient descent play central roles in adjusting the weights of the network based on error rates, optimizing the network’s accuracy over time.
🛠 Hyperparameters such as the number of layers, size of filters, and pooling window sizes are crucial for the network's performance and require careful tuning.
📝 Convolutional neural networks are not universally applicable; they excel where data has a spatial relationship that can be leveraged for pattern recognition.

Q & A

What are convolutional neural networks primarily used for?
-Convolutional neural networks (CNNs) are primarily used for processing data that has a grid-like topology, such as images, where they learn patterns and building blocks that make up the images, such as line segments, angles, and eventually more complex objects like faces or elements of cars.
How do convolutional neural networks handle images that vary in size, rotation, or lighting?
-CNNs handle variations in image size, rotation, or lighting by learning features and patterns at different scales and orientations through multiple layers. This allows them to recognize objects and patterns in images despite such variations.
What role do reinforcement learning algorithms play in conjunction with convolutional neural networks?
-Reinforcement learning algorithms, when paired with convolutional neural networks, can create systems that learn to make decisions or control actions to achieve a goal. Examples include algorithms that play video games, learn to play Go, or control robots.
What is the purpose of pooling in convolutional neural networks?
-Pooling in CNNs reduces the spatial size of the representation, reduces the number of parameters and computation in the network, and helps achieve spatial invariance to input distortions and shifts. Max pooling, a common technique, retains the maximum value in each sub-region of the feature map.
How does the normalization process, specifically using rectified linear units (ReLUs), affect the data in a neural network?
-Normalization using rectified linear units (ReLUs) affects the data by introducing non-linearity to the network without affecting the receptive fields of the convolution layer. It sets all negative values to zero, which helps prevent the vanishing gradient problem and keeps the data well-behaved for subsequent layers.
Why is the spatial organization of data important for convolutional neural networks?
-The spatial organization of data is crucial for CNNs because they capture local spatial patterns in the data. If the spatial arrangement, such as the proximity of pixels in an image, is significant, CNNs can effectively learn and recognize patterns. If spatial organization is irrelevant or lost, CNNs are less useful.
What is the role of fully connected layers in a convolutional neural network?
-Fully connected layers in a CNN serve to classify the images based on the features extracted and processed by the preceding convolutional and pooling layers. Each neuron in a fully connected layer is connected to all activations in the previous layer, allowing it to make final decisions, such as classifying an image into categories.
How do convolutional neural networks learn the weights and features that are necessary for making predictions?
-CNNs learn weights and features through a process of backpropagation and optimization, such as gradient descent. By training on a dataset with known outcomes, the network adjusts its weights and feature detectors through iterative optimization to minimize the error between its predictions and the actual labels.
Can convolutional neural networks be applied to data types other than images?
-Yes, CNNs can be applied to any data that has a grid-like structure or can be represented as such, including audio data (represented as spectrograms) and text data (arranged in a structured format), as long as there is a meaningful spatial organization that the network can learn from.
What are hyperparameters in the context of convolutional neural networks, and how are they determined?
-Hyperparameters in CNNs are the higher-level structural settings of the network, such as the number and size of layers, the number of features in convolutional layers, and the size and stride of pooling layers. They are usually determined through experimentation, validation, and sometimes optimization techniques to find the best performing model configuration.

Outlines

00:00

🤖 Introduction to Convolutional Neural Networks

Convolutional Neural Networks (CNNs) play a pivotal role in the field of artificial intelligence, particularly in image recognition. These networks process images to learn patterns and elements, such as line segments, which are used to recognize more complex features like faces or car elements in subsequent layers. The initial example demonstrates how CNNs can differentiate between simple images of 'X' and 'O' through pattern recognition, despite variations in size, rotation, or shading. The process involves comparing pixel-by-pixel, utilizing convolution to match image segments and identify matches based on feature similarity, showcasing the fundamental operations of filtering and convolution in CNNs.

05:02

🔍 Deep Dive into Convolution Process

This section explains the convolution process in detail, illustrating how features are applied across an image to create a map of matches, known as filtering. Through this method, CNNs generate a set of filtered images for each feature, demonstrating the convolution layer's ability to identify where features match the image. Additionally, the concept of pooling is introduced, specifically max pooling, which reduces the size of the filtered images while retaining essential patterns. This compression step is crucial for managing computational resources and maintaining the integrity of the image's features.

10:02

🧠 Understanding Normalization and Neural Network Layers

Normalization, particularly through the use of rectified linear units (ReLU), is highlighted as a method to prevent unmanageably large numbers in CNNs by adjusting negative values to zero. This section also outlines how the output of one layer serves as the input for the next, maintaining a structured array of numbers throughout the network. By repeatedly applying convolution, ReLU, and pooling layers in various configurations, CNNs can develop complex patterns recognition capabilities. This part of the process emphasizes the sequential and interconnected nature of neural network layers in achieving refined image recognition.

15:03

🎲 Building and Understanding Neurons in Neural Networks

This segment delves into the construction of neurons within neural networks, illustrating the process of summing inputs, applying weights, and squashing the results to fit within a specific range using functions like the sigmoid. The discussion extends to how layers of neurons can create complex receptive fields, enabling the recognition of patterns such as solid colors, verticals, and diagonals. The concept of backpropagation is touched upon, hinting at its role in adjusting neuron weights based on error rates, thereby enhancing the network's ability to accurately classify inputs.

20:06

🧩 Advanced Neural Network Architectures

This paragraph expands on neural network complexity by exploring additional layers and the process of stacking neurons to create intricate patterns and classifications. It explains how neurons with varying weights and squashing functions contribute to the network's overall ability to discern between complex patterns. The importance of rectified linear units and their role in simplifying the activation function to improve computational efficiency is also discussed. This section underscores the adaptability and depth of neural networks through layered configurations and varied activation functions.

25:08

🔄 Optimization and Gradient Descent Explained

Optimization techniques, especially gradient descent, are elucidated through an analogy of finding the optimal tea drinking temperature. This metaphor simplifies the concept of minimizing error (or maximizing pleasure) by adjusting variables (temperature) based on feedback. The principle extends to neural networks, where gradient descent is used to fine-tune weights and minimize the error function. Challenges such as local minima and the necessity for diverse optimization strategies like genetic algorithms are discussed, highlighting the complexities of neural network training.

30:09

🎯 Fine-Tuning Neural Networks with Backpropagation

The intricate process of backpropagation is detailed as a method for efficiently training neural networks by calculating gradients for each weight. This involves understanding the impact of each weight on the error rate and adjusting accordingly, without recalculating the entire network's output. The text describes how backpropagation navigates through the network's layers, applying the chain rule of calculus to find the optimal adjustments for minimizing the error function. This process underpins the practical training of neural networks, allowing for the refinement of weights and the network's overall ability to classify inputs accurately.

35:10

🌟 Refining Convolutional Neural Networks

This concluding segment discusses the refinement of CNNs through the adjustment of hyperparameters, such as the number of features per layer, and the dimensions and strides of pooling windows. The narrative emphasizes the trial-and-error nature of optimizing these parameters to achieve the best possible model performance. It also touches on the versatility of CNNs in processing not just images, but any data with spatial relationships, such as audio or text, formatted to resemble images. The limitations of CNNs are also addressed, particularly in data types where spatial arrangement does not convey meaningful information.

Mindmap

Keywords

💡Convolutional Neural Networks (CNNs)

Convolutional Neural Networks (CNNs) are a class of deep neural networks, primarily used to analyze visual imagery. They are particularly known for their ability to pick up on patterns in the input images, such as lines, angles, and eventually more complex structures like faces or objects. CNNs achieve this through a series of layers that apply convolution operations, pooling, and normalization to the input data, breaking down the image into features and using these to make classifications or predictions. The script discusses CNNs as the backbone of modern AI in image recognition, showing their process of learning from images of Xs and Os and how they differentiate between them even when the images are rotated or scaled.

💡Features

In the context of CNNs, 'features' refer to the distinct characteristics or patterns within the data that the network identifies and learns as part of its training process. Initially, these might be simple patterns like edges or colors in an image, but as the network goes deeper, it starts recognizing more complex patterns such as parts of objects. The script describes features as the building blocks that CNNs use to understand images, starting from simple line segments to more complex elements like parts of faces or cars, highlighting the hierarchical nature of learning in CNNs.

💡Pooling

Pooling is a down-sampling operation used in CNNs to reduce the dimensionality of feature maps, thereby reducing the number of parameters and computation in the network. This operation helps in making the detection of features somewhat invariant to scale and orientation changes. Max pooling, one of the common types of pooling, involves selecting the maximum element from the region of the feature map covered by the filter. The script explains how pooling shrinks the filtered images by taking the maximum value in each window, simplifying the network while maintaining the essential features.

💡Normalization

Normalization, specifically referred to in the script as using a rectified linear unit (ReLU), is the process of adjusting the scale of data points in neural networks. This operation increases the non-linearity in the network without affecting the receptive fields of the convolution layer. By setting negative values to zero, it helps prevent the issue of vanishing or exploding gradients, making the training process more stable and efficient. The script highlights normalization as a key step in CNNs that keeps the numerical calculations well-behaved and manageable.

💡Fully Connected Layer

A fully connected layer is a neural network layer where every neuron is connected to every neuron in the previous layer. This layer is typically used toward the end of CNN architectures to classify the features extracted by the convolutional and pooling layers into the final output categories. The script describes how, after several iterations of convolution and pooling, the network uses a fully connected layer to weigh the significance of various features for the classification task, exemplifying how each pixel value votes on the output category based on learned weights.

💡Backpropagation

Backpropagation is a fundamental algorithm for training neural networks, particularly used in the context of supervised learning. It efficiently computes the gradient of the loss function with respect to each weight by the chain rule, allowing for the optimization of weights in the network. This process involves moving backwards through the network, from the output to the input layer, adjusting weights to minimize the error between the predicted and actual outputs. The script details backpropagation as the method by which CNNs learn from examples, adjusting weights to reduce classification errors.

💡Gradient Descent

Gradient descent is an optimization algorithm used to minimize the loss function in neural networks. It works by iteratively moving towards the minimum of the loss function in the direction of the steepest descent as defined by the negative of the gradient. The script illustrates gradient descent metaphorically with tea temperature optimization, demonstrating how one can use the algorithm to find the ideal parameters that minimize the error in predictions, by making small, directed adjustments based on the gradient.

💡Hyperparameters

Hyperparameters are the configuration settings used to structure the neural network, which influence the network's architecture and the learning process but are not updated during training. These include choices like the number of layers, the number of neurons in each layer, the learning rate, and the size of the convolutional filters. The script points out that hyperparameters are crucial for the performance of CNNs, dictating how the network learns and performs, yet must often be determined through experimentation and optimization.

💡Loss Function

A loss function, also known as a cost function, measures the difference between the network's predicted output and the actual output, providing a metric to evaluate the performance of the neural network. Minimizing the loss function is the goal of training a neural network. The script discusses the concept of a loss function through the example of estimating the number of M&Ms in a bag, showing how optimization algorithms like gradient descent use the loss function to guide the training process towards more accurate predictions.

💡Receptive Field

The receptive field in the context of CNNs refers to the specific region of the input data that a particular CNN feature is looking at when computing a convolution operation. It represents the extent of the input space that affects a particular feature in the output feature map. The script uses the concept of a receptive field to explain how individual neurons in the network are influenced by certain parts of the input image, and how this concept is foundational in building complex patterns recognition in layers of the network.

Highlights

Convolutional Neural Networks (CNNs) are pivotal in the understanding and development of Artificial Intelligence, primarily used for image recognition and analysis.

CNNs identify and learn patterns and building blocks in images, such as line segments and angles, progressing to complex objects like faces or car elements.

Combining CNNs with reinforcement learning algorithms enables advanced applications like video game automation, playing board games like Go, and robotics control.

A simple CNN example demonstrates the network's ability to differentiate between images of an 'X' or an 'O', adjusting for variations in size, rotation, and brightness.

CNNs process images through filtering, using convolution layers to match and identify features within the image, enhancing pattern recognition.

Pooling layers in CNNs reduce the size of the processed images while maintaining the essence of the image's features, improving computational efficiency.

Normalization, specifically through rectified linear units, ensures the mathematical stability of CNNs by adjusting negative values to zero across layers.

CNN architectures can be intricately layered, with each layer's output feeding into the next, allowing for deep and complex pattern analysis.

The optimization of CNNs involves gradient descent and backpropagation, fine-tuning the network's weights based on the error or loss function.

Hyperparameters in CNNs, such as the number and size of filters or layers, significantly influence the network's performance and accuracy.

Convolutional layers, pooling layers, and fully connected layers each play a unique role in a CNN, collectively contributing to the network's ability to classify images accurately.

Machine learning and optimization techniques in CNNs are grounded in mathematical principles, including calculus and linear algebra, to adjust weights and reduce error.

CNNs are not limited to image processing; they can be applied to any data with spatial relationships, including audio and textual information, by representing the data in a structured format similar to images.

The adaptability and effectiveness of CNNs are rooted in their ability to learn from examples, adjusting features and weights to improve classification accuracy over time.

Advanced applications and research in CNNs explore optimizing network architectures and hyperparameters, continually enhancing their capabilities and finding new applications.

Transcripts

Browse More Related Video

Convolutional Neural Networks Explained (CNN Visualized)

MIT 6.S191 (2023): Convolutional Neural Networks

How to Create a Neural Network (and Train it to Identify Doodles)

Neural Networks: Crash Course Statistics #41

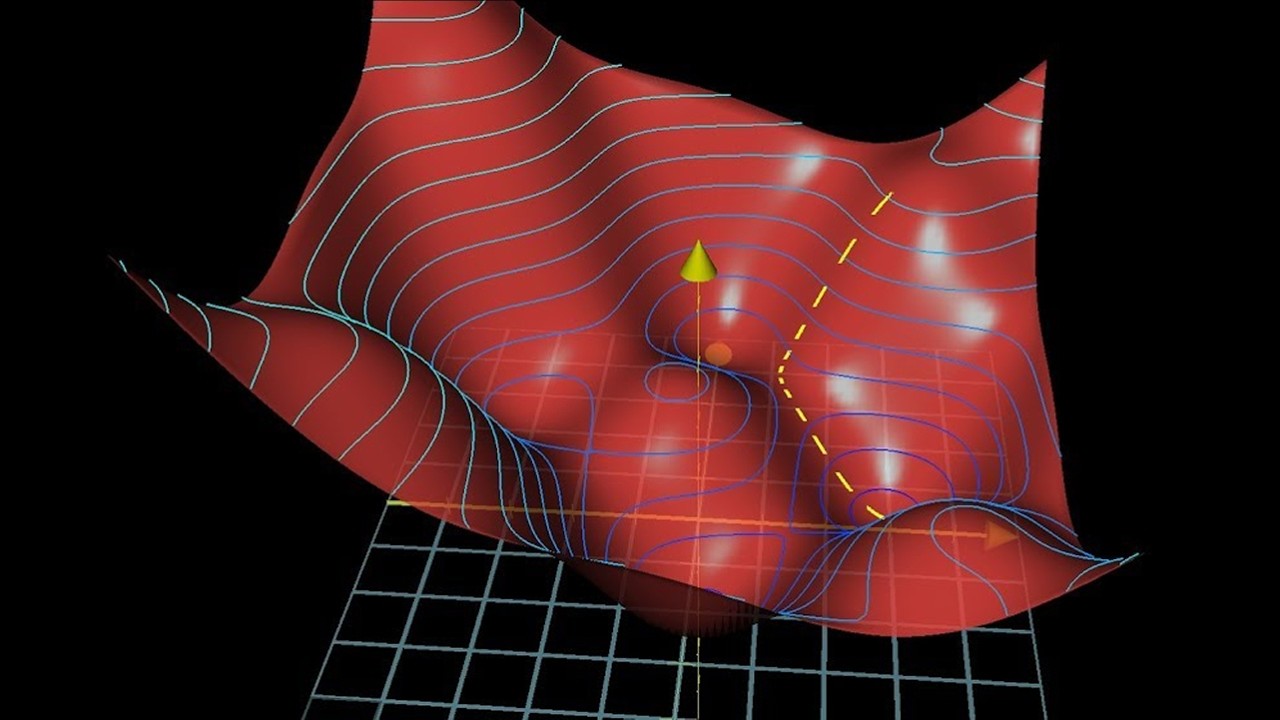
Gradient descent, how neural networks learn | Chapter 2, Deep learning

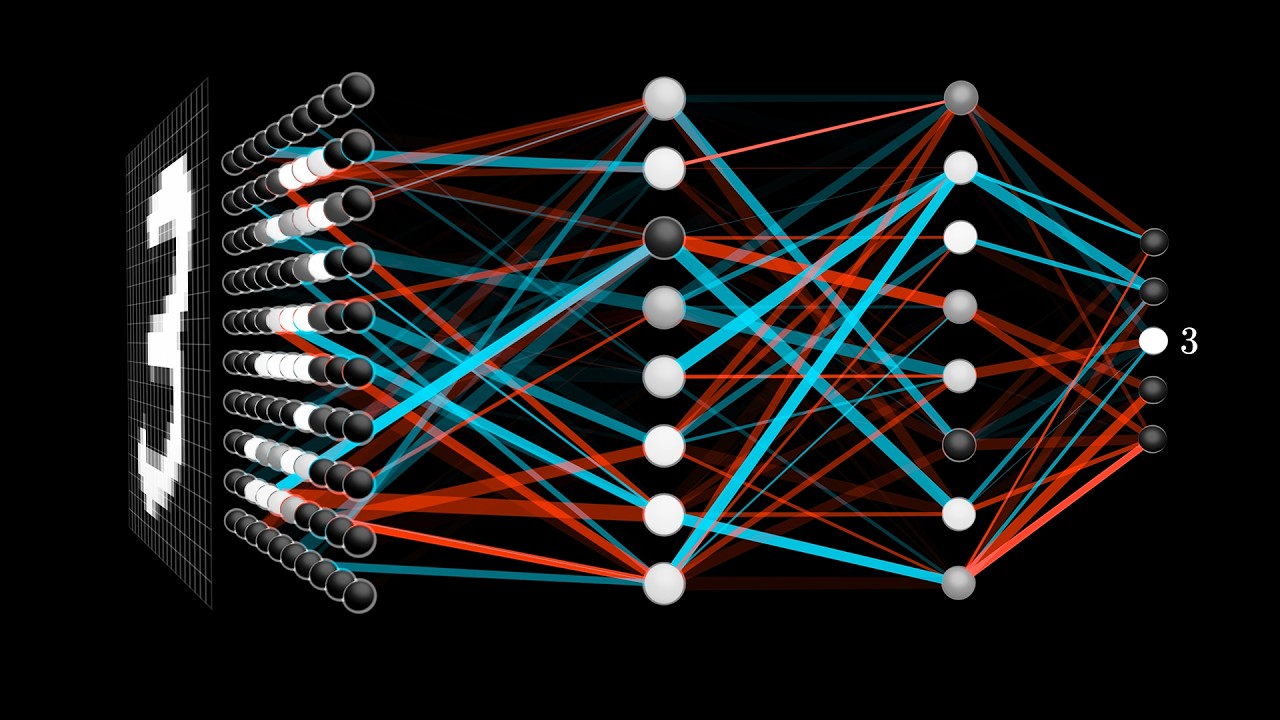
But what is a neural network? | Chapter 1, Deep learning

Related Tags

Artificial Intelligence CNNs Image Recognition Optimization Machine Learning Deep Learning Neural Networks Data Analysis Pattern Recognition Tech Innovation