Gradient descent, how neural networks learn | Chapter 2, Deep learning
TLDRThis video script delves into the fundamentals of neural networks, focusing on gradient descent as the core learning mechanism. It explains how a network with two hidden layers can recognize handwritten digits, highlighting the process from random initialization to minimizing the cost function for better performance. The script also touches on the limitations of traditional networks, suggesting that despite their success, they may not learn in the intuitive pattern-recognition way humans expect. It concludes by encouraging deeper engagement with the material and references to modern research for a more nuanced understanding of neural networks.
Takeaways
- 🧠 The video script provides an overview of neural networks, focusing on their structure and learning process, particularly in the context of handwritten digit recognition.
- 📉 The concept of gradient descent is introduced as a fundamental algorithm for machine learning, which is used to minimize the cost function and improve network performance.
- 🔍 The script explains the role of hidden layers in a neural network, suggesting that they might detect edges, patterns, and ultimately recognize digits, although the actual mechanism may differ from this expectation.
- 🎯 The goal of training a neural network is to adjust its weights and biases to minimize the cost function, which measures the network's performance on training data.
- 📈 The cost function is calculated as the average of the squared differences between the network's output and the desired output for all training examples.
- 🔢 The network's weights and biases are initialized randomly, which initially leads to poor performance, but are iteratively improved through the learning process.
- 📊 The script discusses the importance of the cost function having a smooth output to facilitate the gradient descent process and the finding of a local minimum.
- 🤖 The backpropagation algorithm is mentioned as the method for efficiently computing the gradient of the cost function, which is central to how neural networks learn.
- 📚 The video encourages active learning and engagement with the material, suggesting modifications to the network and exploring resources like Michael Nielsen's book on deep learning.
- 🔬 The script touches on the idea that modern neural networks may not learn in the intuitive way we expect, as evidenced by experiments where networks memorize data rather than understanding patterns.
- 🌐 It concludes with a discussion on the optimization landscape of neural networks, suggesting that local minima may be of equal quality, making it easier to find good solutions when the dataset is structured.
Q & A
What are the two main goals of the video script?
-The two main goals are to introduce the concept of gradient descent, which is fundamental to neural networks and other machine learning techniques, and to delve deeper into how the specific neural network operates, particularly what the hidden layers of neurons are looking for.
What is the classic example of a neural network task mentioned in the script?
-The classic example mentioned is handwritten digit recognition, often referred to as the 'hello world' of neural networks.
How are the inputs for a neural network structured in the context of the script?
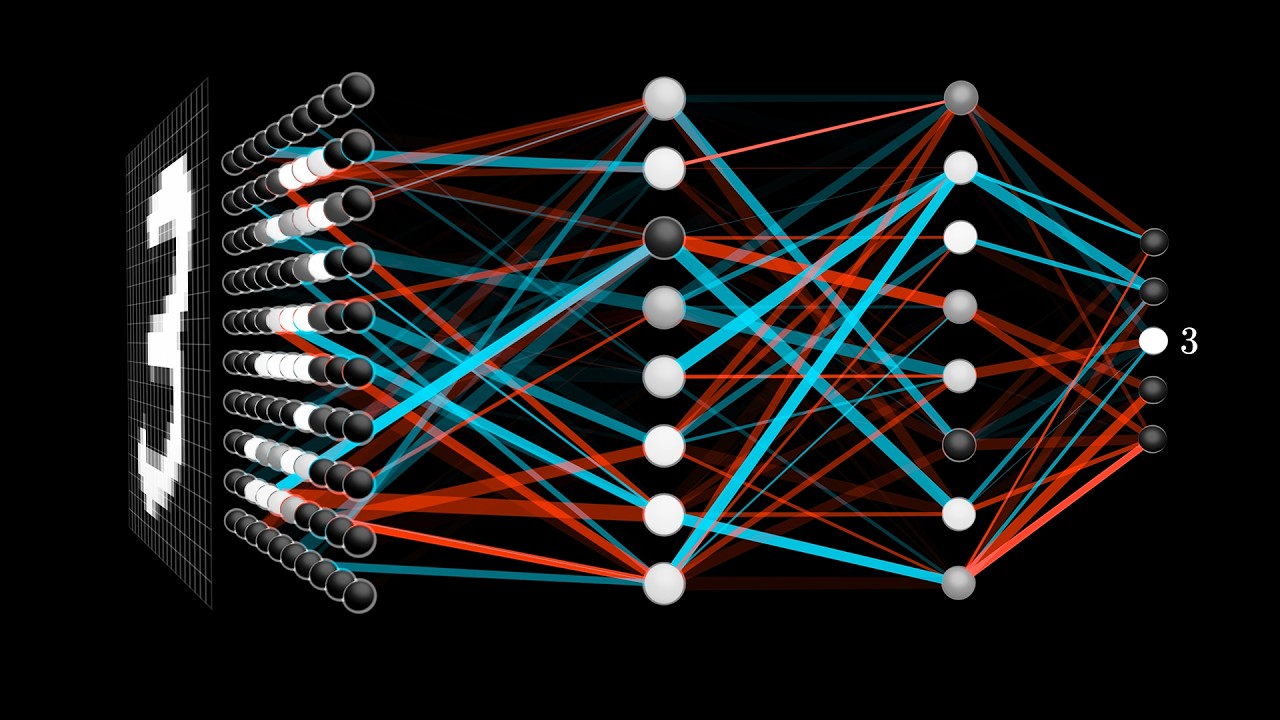
-The inputs are structured as a 28x28 pixel grid, where each pixel has a grayscale value between 0 and 1, determining the activations of 784 neurons in the input layer of the network.
What is the role of the activation function in a neural network?
-The activation function, such as sigmoid or relu, is used to transform the weighted sum of activations from the previous layer, along with a bias, to determine the activation of neurons in the current layer.
What is the purpose of the bias in a neural network?
-The bias is a special number that indicates the tendency of a neuron to be active or inactive, adjusting the weighted sum of inputs to the neuron.
How many weights and biases does the network described in the script have?
-The network has approximately 13,000 weights and biases, which are adjustable values that determine the network's behavior.
What does the final layer of neurons in the network represent?
-The final layer of neurons represents the classification of the input digit, with the brightest neuron corresponding to the recognized digit.
What is the purpose of the cost function in training a neural network?
-The cost function measures the error between the network's output and the desired output for a given training example, providing a way to evaluate and improve the network's performance.
How does the script describe the initialization of weights and biases in a neural network?
-The weights and biases are initialized randomly, which initially results in poor performance until they are adjusted through training.
What is gradient descent, and how does it relate to neural network learning?
-Gradient descent is a method for minimizing a cost function by iteratively adjusting the weights and biases in the direction opposite to the gradient, effectively finding a local minimum that improves the network's performance.
What does the script suggest about the actual functioning of the neural network in recognizing digits?
-The script suggests that despite the network's success in recognizing digits, it does not necessarily pick up on the expected patterns like edges or loops, and its confidence in its decisions is not indicative of the actual correctness of those decisions.
How does the script address the memorization versus understanding debate in neural networks?
-The script discusses a study where a deep neural network was trained on a dataset with shuffled labels, which it memorized to achieve the same training accuracy as with a properly labeled dataset, raising questions about whether the network truly understands the data or is merely memorizing it.
Outlines
🧠 Neural Network Structure and Gradient Descent Introduction
This paragraph outlines the structure of a neural network, focusing on the example of handwritten digit recognition using the MNIST database. It explains the input layer with 784 neurons representing pixel values, the subsequent layers with weighted sums and activation functions like sigmoid or relu, and the output layer with 10 neurons corresponding to digits. The network's performance is determined by about 13,000 adjustable weights and biases. The paragraph introduces the concept of gradient descent, a fundamental algorithm for machine learning that minimizes a cost function by iteratively adjusting these parameters based on the error between predicted and actual outputs. The goal is to improve the network's performance on training data and ensure that it generalizes well to new, unseen data.
📉 Understanding Gradient Descent and Function Minimization
The second paragraph delves into the mechanics of gradient descent as a method for minimizing the cost function of a neural network. It starts by simplifying the concept with a single-variable function and then extends it to multivariable functions, highlighting the role of the gradient in indicating the direction of steepest descent. The gradient's magnitude and direction are crucial for adjusting the network's weights and biases efficiently. The paragraph emphasizes that minimizing the cost function, which averages the error over all training examples, is the core of learning in neural networks. It also touches on the challenges of local minima and the importance of the cost function's smoothness for effective gradient descent.
🔍 The Role of Gradient in Neural Network Learning
This paragraph explores the significance of the gradient in the context of neural network learning. It discusses how the negative gradient vector encodes the relative importance of each weight and bias in the network, guiding the adjustments that will most significantly reduce the cost function. The paragraph uses the analogy of a ball rolling down a hill to illustrate the process of gradient descent, emphasizing that the components of the gradient vector not only indicate the direction for optimization but also the relative impact of each parameter change. It also reflects on the actual performance of a simple neural network with two hidden layers, noting that while it can achieve high accuracy on new images, the learned patterns may not align with human expectations of recognizing edges and structures.
🤖 Limitations of Early Neural Networks and the Path Forward
The final paragraph addresses the limitations of early neural network architectures and the evolution towards modern deep learning techniques. It points out that while basic neural networks can achieve reasonable accuracy, their understanding of images is superficial and lacks the depth of human perception. The paragraph suggests that these networks are more about memorization than true learning, as evidenced by their confident yet incorrect classifications of random images. It encourages viewers to engage with the material, consider improvements, and explore resources like Michael Nielsen's book on deep learning. It also references recent research that delves into how modern neural networks learn and the nature of the optimization landscape they navigate during training.
Mindmap
Keywords
💡Neural Network
💡Gradient Descent
💡Hidden Layers
💡Activation
💡Weights
💡Bias
💡Cost Function
💡Backpropagation
💡MNIST Database
💡Generalization
💡Feature Extraction
Highlights
Introduction to the concept of gradient descent, fundamental to neural networks and machine learning.
Exploration of a neural network's hidden layers and their role in recognizing patterns in handwritten digit images.
Handwritten digit recognition as the 'hello world' of neural networks, using a 28x28 pixel grid with grayscale values.
Activation of neurons based on a weighted sum of previous layer activations and a bias, followed by a non-linear function.
Network architecture with two hidden layers of 16 neurons each, totaling approximately 13,000 adjustable weights and biases.
The network's classification of digits based on the highest activation in the final layer of neurons.
The layered structure's potential for recognizing edges, loops, lines, and assembling them to identify digits.
Training the network with labeled data to adjust weights and biases for improved performance.
Generalization of learned patterns beyond the training data, tested with new, unseen images.
Use of the MNIST database for training, containing tens of thousands of labeled handwritten digit images.
The cost function as a measure of the network's performance, based on the difference between expected and actual outputs.
Gradient descent as a method for minimizing the cost function by adjusting weights and biases.
Backpropagation as the algorithm for efficiently computing the gradient, central to neural network learning.
The importance of a smooth cost function for effective gradient descent and finding local minima.
Continuously ranging activations of artificial neurons versus binary activations of biological neurons.
Network performance on new images with a simple structure reaching up to 96% accuracy.
Potential improvements to the network's architecture to enhance recognition of edges and patterns.
The network's inability to understand or draw digits despite successful recognition, highlighting its limitations.
Discussion on the memorization capabilities of deep neural networks and their ability to learn structured data.
Transcripts
Browse More Related Video

How to Create a Neural Network (and Train it to Identify Doodles)
But what is a neural network? | Chapter 1, Deep learning

MIT Introduction to Deep Learning | 6.S191

Neural Networks: Crash Course Statistics #41

Convolutional Neural Networks Explained (CNN Visualized)

The Chain Rule for Derivatives — Topic 59 of Machine Learning Foundations
5.0 / 5 (0 votes)
Thanks for rating: