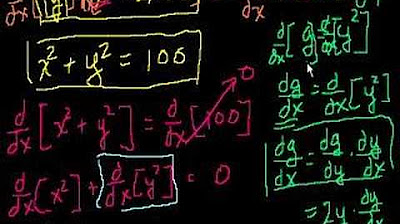Showing explicit and implicit differentiation give same result | AP Calculus AB | Khan Academy

Khan Academy
30 Jan 201307:48
EducationalLearning
32 Likes 10 Comments

TLDRThe video script demonstrates the process of both explicit and implicit differentiation, using the relationship x times the square root of y equals 1 as an example. It shows that both methods yield the same result, with explicit differentiation leading to y being 1 over x squared, and implicit differentiation resulting in the expression for dy/dx involving y and x. The video emphasizes the power of substitution to confirm the equivalence of the two differentiation approaches.

Takeaways
  • 📚 Implicit differentiation can yield the same results as explicit differentiation when possible.
  • 🔢 The relationship given, x * √y = 1, is easily solved explicitly for y, resulting in y = 1/x².
  • 📈 To find the derivative of y with respect to x, the chain rule is applied, yielding dy/dx = -2x^(-2.5).
  • 🌟 The video demonstrates the process of differentiating the same equation implicitly.
  • 🤔 When differentiating implicitly, both the product rule and chain rule are applied to the left-hand side of the equation.
  • 🧠 The derivative of the constant on the right-hand side of the equation is zero, simplifying the implicit differentiation process.
  • 📊 The derivative with respect to x of x is 1, simplifying the left-hand side of the implicit differentiation equation.
  • 🔄 The process simplifies to dy/dx being expressed in terms of y and x derivatives.
  • 👉 By substituting y = 1/x² back into the implicitly derived expression, it matches the explicitly derived result.
  • 🎯 The key insight is that implicit differentiation, when solvable explicitly, aligns with the results from explicit differentiation.
  • 📝 The video script serves as a comprehensive guide for understanding the process and application of implicit differentiation.
Q & A

  • What is the main point the speaker is trying to make in the video?

    -The speaker aims to demonstrate that implicit differentiation can yield the same results as explicit differentiation when an explicit solution is available.

  • What is the given relationship between x and y in the video?

    -The relationship is x times the square root of y equals 1.

  • How does the speaker solve for y explicitly?

    -By dividing both sides by x, the speaker finds that the square root of y equals 1/x. Upon squaring both sides, it results in y equals 1/x squared, or x to the negative 2 power.

  • What is the derivative of y with respect to x using explicit differentiation?

    -Using explicit differentiation and the chain rule, the derivative is dy/dx = -2x to the negative 2 minus 1, or -2x to the negative 3 power.

  • How does the speaker apply the derivative operator to the equation in implicit differentiation?

    -The speaker applies the derivative operator to both sides of the equation, using the product rule for the left-hand side and recognizing the derivative of the constant on the right-hand side as 0.

  • What is the result of the implicit differentiation?

    -The result of implicit differentiation is (dy/dx) times the derivative of y with respect to x equals negative square root of y.

  • How does the speaker simplify the result of implicit differentiation?

    -The speaker simplifies by subtracting the square root of y from both sides and solving for dy/dx, eventually obtaining -2y over x times the negative square root of y.

  • What is the key insight the speaker provides to reconcile the difference between explicit and implicit differentiation results?

    -The speaker points out that the result from implicit differentiation can be made equivalent to the explicit differentiation result by substituting y with 1/x squared, which shows they are the same.

  • What is the significance of the video in understanding differentiation?

    -The video emphasizes the understanding that both explicit and implicit differentiation methods can yield the same results, and it showcases the process of applying each method to a given function.

  • How does the video script contribute to the understanding of the chain rule?

    -The video script provides a clear example of applying the chain rule in both explicit and implicit differentiation, highlighting how it's used to find the derivative of a composite function.

Outlines
00:00
📚 Introduction to Implicit Differentiation

The paragraph introduces the concept of implicit differentiation and compares it with explicit differentiation. It sets up a scenario where the relationship between x and y is given by the equation x times the square root of y equals 1. The speaker explains how to solve for y explicitly by applying algebraic manipulation and then proceeds to differentiate both sides of the equation implicitly to find the derivative of y with respect to x. The process involves using the product rule and chain rule, and the goal is to demonstrate that both differentiation methods yield the same result.

05:02
🔢 Solving for the Derivative Implicitly

This paragraph delves into the process of implicitly differentiating the given equation to find the derivative of y with respect to x. The speaker begins by applying the derivative operator to both sides of the equation, explaining the use of the product rule and chain rule in detail. After simplifying the expression, the speaker isolates the term involving the derivative of y with respect to x. Through further algebraic manipulation and by making a substitution back into the original equation, the speaker shows that the result obtained from implicit differentiation is consistent with the result from explicit differentiation, thus validating the process.

Mindmap
Keywords
💡Implicit Differentiation
Implicit differentiation is a method used to find the derivative of a function when the function is not explicitly expressed in terms of one variable. In the video, the process is demonstrated by differentiating the equation x * sqrt(y) = 1 without solving for y explicitly, which aligns with the main theme of showing that implicit differentiation can yield the same results as explicit differentiation when possible.
💡Explicit Differentiation
Explicit differentiation refers to the process of finding the derivative of a function when it is expressed directly in terms of a single variable. This is contrasted with implicit differentiation in the video, where the presenter first demonstrates how to differentiate the same equation x * sqrt(y) = 1 by explicitly solving for y, and then comparing it to the result obtained through implicit differentiation.
💡Chain Rule
The chain rule is a fundamental principle in calculus used to find the derivative of a composite function. It states that the derivative of a function composed of other functions is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is applied when differentiating y with respect to x in the context of both explicit and implicit differentiation.
💡Product Rule
The product rule is a calculus technique used to find the derivative of a product of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the video, the product rule is applied when differentiating the left-hand side of the equation x * sqrt(y) with respect to x.
💡Derivative Operator
The derivative operator, often denoted by d/dx or ∂, represents the operation of finding the derivative of a function with respect to a variable, typically x. It is a fundamental concept in calculus and is central to both explicit and implicit differentiation discussed in the video.
💡Square Root
A square root is a mathematical operation that finds a value which, when multiplied by itself, gives the original number. In the context of the video, the square root is used in the original equation and in the process of differentiating with respect to x.
💡Power Rule
The power rule is a basic rule in calculus that allows the differentiation of functions raised to a power. It states that the derivative of x^n, where n is any real number, is n * x^(n-1). The power rule is used in the video when differentiating the explicit form of y, y = 1/x^2, to obtain dy/dx = -2x^(-3).
💡Solving for Derivative
Solving for the derivative involves finding the rate of change or the slope of a function at a particular point. In the video, the process of solving for the derivative focuses on both explicitly and implicitly differentiating the given equation to compare the results and demonstrate the equivalence of the two methods.
💡Substitution
Substitution is a mathematical method used to simplify equations by replacing one or more variables with equivalent expressions. In the video, substitution is suggested as a way to confirm the equivalence of the results obtained from explicit and implicit differentiation by replacing y with its explicit form derived from the equation x * sqrt(y) = 1.
💡Differentiation
Differentiation is a fundamental process in calculus that involves finding the derivative of a function, which represents the rate of change or the slope of the function at any point. The video focuses on demonstrating the process of differentiation through both explicit and implicit methods.
💡Rate of Change
The rate of change, or the derivative, represents the speed at which a function changes with respect to its variable. It is a core concept in calculus and is the focus of the video, where the derivative dy/dx is calculated to understand how the function y changes as x varies.
Highlights

The video demonstrates the process of implicit differentiation and compares it with explicit differentiation.

The relationship x times the square root of y equals 1 is used to illustrate the differentiation process.

Explicit differentiation is shown by solving for y, resulting in y equals 1 over x squared.

The derivative of y with respect to x is calculated using the chain rule in explicit differentiation, yielding dy/dx = -2x^(-2 - 1).

Implicit differentiation is applied to the same equation to see if it yields the same result.

The product rule and chain rule are used when differentiating the left-hand side of the equation implicitly.

The derivative of the constant term on the right-hand side is zero, simplifying the implicit differentiation process.

The chain rule is applied to the derivative of the square root of y with respect to x.

The derivative with respect to x of the square root of y is found to be (1/2)y^(-1/2).

The entire chain rule is applied to find the derivative of the expression with respect to x.

The equation is simplified by subtracting the square root of y from both sides.

The derivative dy/dx is isolated and solved for by dividing both sides by a specific expression.

The final result of the implicit differentiation is -2y/x, which looks different from the explicit result.

A substitution is made to show that the implicit and explicit differentiation results are the same.

The substitution reveals that -2y/x is equivalent to -2x^(-3), confirming the consistency of both differentiation methods.

Transcripts

Browse More Related Video

Implicit Differentiation Method

Introduction to Implicit Differentiation

Implicit Differentiation

Implicit Differentiation

Implicit Differentiation for Calculus - More Examples #2

Math 11 - Section 3.8

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus TechniquesImplicit DifferentiationExplicit DifferentiationMathematical AnalysisDerivative CalculationEducational ContentMath TutorialChain Rule ApplicationProduct Rule ExplanationAlgebraic Manipulation