Volume with cross sections: intro | Applications of integration | AP Calculus AB | Khan Academy
TLDRThe video script introduces the concept of finding the volume of a three-dimensional shape, where the base is defined by the area between two curves. The instructor illustrates this by creating a shape with a square cross-section, using the difference between the functions y=6 and y=4*ln(3-x) as the height and base length. The volume is calculated by breaking the shape into infinitesimally small square tiles (dx) and integrating the product of their depth, base area, and height from x=0 to x=2. The integral's evaluation yields an approximate volume of 26.27 cubic units, demonstrating the power of integration in solving complex geometric problems.
Takeaways
- 📚 The video tutorial focuses on finding the volume of three-dimensional shapes, a step beyond the basic concept of calculating the area between curves.
- 🔍 Viewers are encouraged to review the foundational concept of finding areas between curves on Khan Academy if they are not familiar with it.
- 📏 The example provided involves a shape with its base defined by the area between two curves, extending the concept into three dimensions.
- ✏️ The base of the shape in the example is the region between the line y=6 and the curve y=4ln(3-x), with x ranging from 0 to 2.
- 📐 The three-dimensional shape is described as having square cross sections perpendicular to the x-axis, with the side length equal to the difference between the two functions at any given x.
- 💡 The tutorial demonstrates how to calculate the volume of such a shape by integrating the square of the difference between the two functions over the given range of x.
- 🔢 The specific integral to calculate the volume is from x=0 to x=2 of (6-4ln(3-x))^2 dx, representing the sum of the volumes of infinitesimally thin square-based prisms along the x-axis.
- 🖩 The calculation of the definite integral, potentially complex to solve by hand, is illustrated using a calculator function for convenience and accuracy.
- 📊 The result of the integral, approximately 26.27, represents the volume of the shape in cubic units, showcasing the practical application of integration in three-dimensional geometry.
- 👩🏫 The video aims to demystify the concept of integrating in three dimensions by breaking down the process into understandable steps, encouraging viewers to leverage their knowledge of integration.
Q & A
What is the main topic of the video?
-The main topic of the video is finding the volume of a three-dimensional shape where the base is defined by the area between two curves.
How does the instructor suggest finding the area between curves?
-The instructor suggests using a definite integral to find the area between curves, as demonstrated on Khan Academy.
What is the shape being discussed in the video?
-The shape being discussed is a three-dimensional figure with a square cross-section, formed by the area between two functions.
What are the two functions used to define the base of the shape?
-The two functions used are y = 6 and y = 4 times the natural log of (3 - x).
How is the height of each small square tile determined?
-The height of each small square tile is determined by the difference between the two functions at a given x-value.
What is the formula for calculating the volume of one of the small square tiles?
-The volume of one of the small square tiles is calculated as the depth (dx) times the base length squared (the difference of the two functions squared).
How does the instructor suggest finding the volume of the entire shape?
-The instructor suggests finding the volume of the entire shape by integrating the volume of the small square tiles from x equals zero to x equals two.
What is the significance of using definite integrals in this context?
-Definite integrals are used to sum up the volumes of the infinitesimally small tiles that make up the shape, allowing for the calculation of the total volume.
How does the video demonstrate the power of integration?
-The video demonstrates the power of integration by showing how it can be used to calculate complex volumes that are not easily determined by traditional geometric methods.
What is the approximate volume of the shape obtained from the integral?
-The approximate volume of the shape obtained from the integral is 26.27 cubic units.
How can one evaluate the definite integral shown in the video?
-One can evaluate the definite integral by using a calculator, inputting the appropriate functions, and integrating with respect to x over the given interval.
Outlines
📚 Introduction to Volume Calculation with Definite Integrals
This paragraph introduces the concept of calculating the volume of three-dimensional shapes, where the base is defined by the area between two curves. The instructor explains that although the viewer may be familiar with finding the area between curves, this video will explore a more interesting application, which is finding the volume of such shapes. The shape in question has a square cross-section, with the height determined by the difference between the two functions that define the base. The process involves breaking the shape into small square tiles with depth dx and calculating their volumes before summing them up to find the total volume using a definite integral.
🔢 Calculating the Volume with Definite Integrals
In this paragraph, the calculation process is detailed. The instructor explains how to find the volume of one of the small square tiles that make up the shape. The volume is calculated by multiplying the depth (dx) by the area of the cross-section, which is the squared difference between the two functions defining the base of the shape. The integral is then evaluated using a calculator, with the result giving the volume of the entire shape. The final result is approximately 26.27 cubic units, emphasizing the power of definite integrals in solving complex volume problems.
Mindmap
Keywords
💡Definite Integral
💡Area Between Curves
💡Three-Dimensional Shape
💡Cross-Section
💡Natural Logarithm
💡Volume
💡Integration
💡Square Cross-Section
💡Difference of Functions
💡Depth (dx)
💡Calculator
Highlights
Introduction to finding the volume of shapes with bases defined by the area between two curves.
Explanation of creating a three-dimensional shape with a square cross section.
Description of how the base is defined by the area between the line y=6 and the graph of y=4*ln(3-x).
Illustration of a shape in three dimensions with perspective to highlight its volume.
Introduction to the concept of cross sections being squares.
The process of calculating volume by considering small square tiles with depth.
Explanation of using integration to calculate the volume of the shape.
Formula for the volume of a small section of the shape.
How to integrate to find the volume of the entire shape.
Explanation of squaring the difference between functions to calculate surface area of the 3D shape.
Step-by-step guide on setting up the definite integral to find the volume.
Demonstration of calculating the definite integral using a calculator.
Final result of the volume calculation.
Understanding the significance of the calculated volume in terms of cubic units.
Encouragement for viewers to explore three-dimensional integration.
Transcripts
Browse More Related Video

Volume with cross sections: squares and rectangles (no graph) | AP Calculus AB | Khan Academy

Disc method around x-axis | Applications of definite integrals | AP Calculus AB | Khan Academy
2013 AP Calculus AB Free Response #5
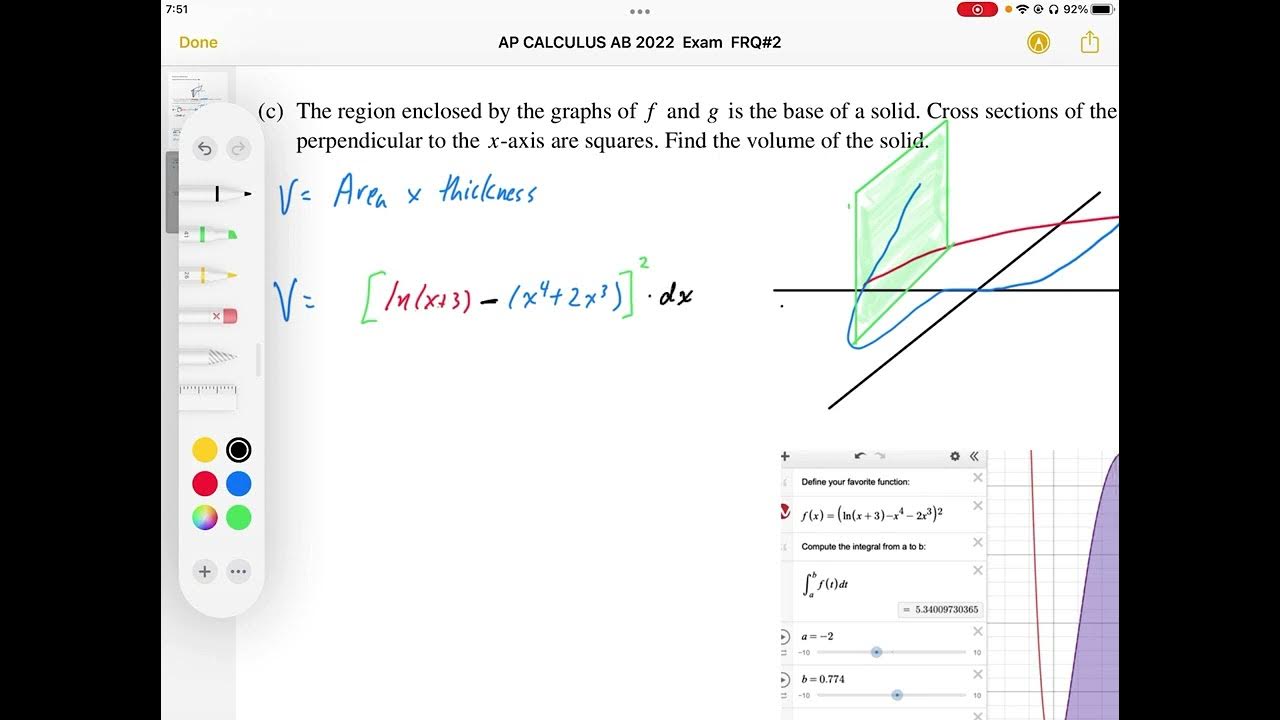
AP CALCULUS AB 2022 Exam Full Solution FRQ#2c

Area Between y=x^3 and y=3x-2 | MIT 18.01SC Single Variable Calculus, Fall 2010

Finding the Volumes of Known Cross Sections ❖ AP Calculus AB
5.0 / 5 (0 votes)
Thanks for rating: