2011 Calculus BC free response #3a | AP Calculus BC | Khan Academy

Khan Academy
13 Sept 201105:41
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the problem of finding the perimeter of a region R in the first quadrant, defined by the graph of the function f(x) = e^(2x), the coordinate axes, and the vertical line x = k. The key to solving this problem lies in understanding the arc length formula and applying it to the curve defined by the function. The script provides a detailed explanation of how to derive the arc length formula from first principles, emphasizing the importance of understanding the underlying calculus concepts. The final expression for the perimeter of R is given in terms of k, without evaluation, highlighting the process of integration and the application of derivatives.

Takeaways
  • The problem involves finding the perimeter of a region R in the first quadrant bounded by the graph of the function f(x) = e^(2x), the coordinate axes, and the vertical line x = k, where k > 0.
  • The perimeter of region R can be expressed using an integral that accounts for the length of the curve, the vertical line, and the horizontal line.
  • The integral expression for the perimeter involves the arc length formula, which is derived using the concept of differentials and the Pythagorean theorem.
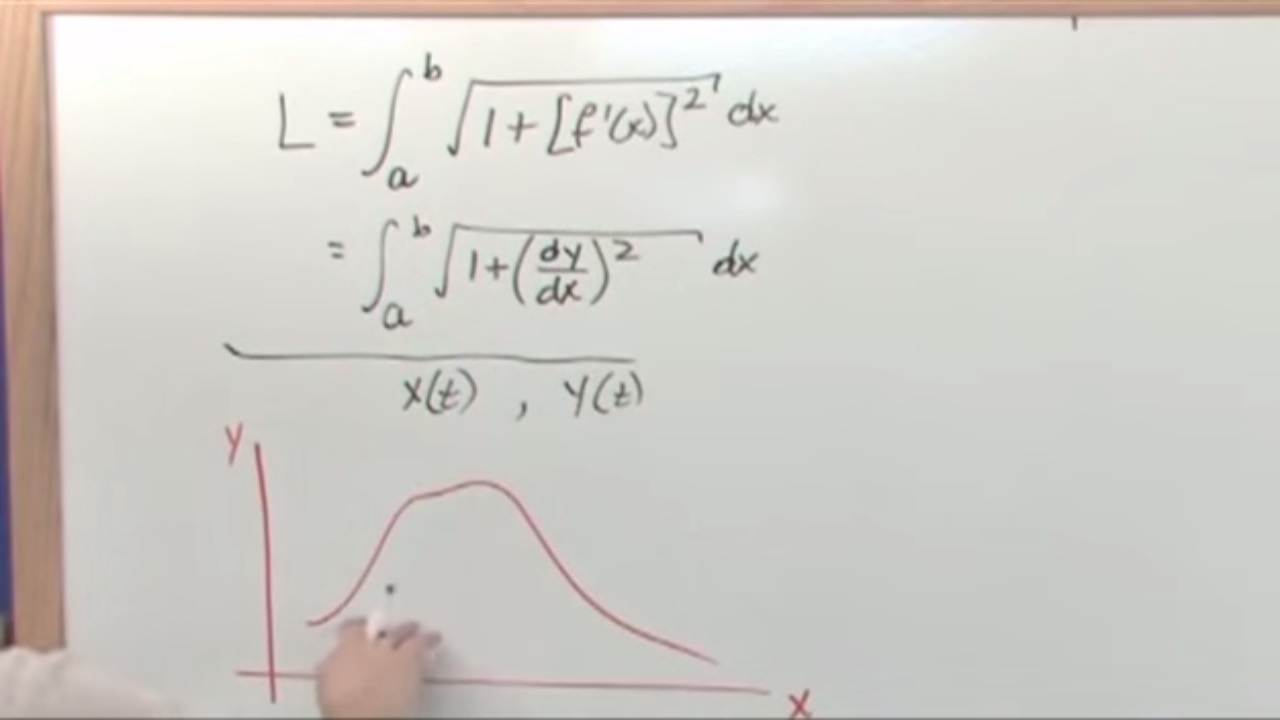
  • The arc length formula for a function is given by the integral of the square root of 1 plus the derivative of the function squared, dx, from 0 to k.
  • The derivative of the given function f(x) = e^(2x) with respect to x is f'(x) = 2e^(2x), which is used in the arc length formula.
  • The perimeter expression includes the length of the vertical line segment which is 1, the horizontal line segment which is k, and the height which is f(k) = e^(2k).
  • The problem requires writing but not evaluating the integral expression, which simplifies the process by focusing on the setup rather than the computation.
  • The script emphasizes the importance of understanding the derivation of formulas like the arc length formula, even outside of academic settings, for better problem-solving and conceptual clarity.
  • The problem and its solution are relevant to calculus, specifically involving concepts of integration and derivatives, and are suitable for an AP exam level of understanding.
  • The script serves as a comprehensive guide to setting up the problem, highlighting the steps and considerations necessary to derive the expression for the perimeter of region R.
Q & A

  • What is the function f(x) defined as in the problem?

    -The function f(x) is defined as e to the power of 2x.

  • What region R is being referred to in the problem?

    -Region R is the area in the first quadrant enclosed by the graph of function f(x), the coordinate axes, and the vertical line x equals k.

  • What is the perimeter of region R in terms of k?

    -The perimeter of region R is given by an integral from 0 to k of the square root of 1 plus (4e to the power of 4x), plus 2(k + e to the power of 2k).

  • How is the arc length formula derived in the script?

    -The arc length formula is derived by considering a small change in x (dx) and y (dy), and using the Pythagorean theorem to approximate the curve length as the square root of (dx^2 + dy^2), where dy is f'(x)dx.

  • What is the derivative of the function f(x) = e^(2x)?

    -The derivative of the function f(x) = e^(2x) with respect to x is f'(x) = 2e^(2x).

  • How is the length of the vertical line segment in the perimeter of R determined?

    -The length of the vertical line segment in the perimeter of R is determined by the value of k, and it is simply k.

  • What is the significance of the integral in the expression for the perimeter of R?

    -The integral in the expression for the perimeter of R represents the sum of the infinitesimally small arc lengths of the curve from x=0 to x=k.

  • What are the two horizontal line segments in the perimeter of R?

    -The two horizontal line segments in the perimeter of R are the segment along the x-axis from the y-axis to the vertical line x=k, and the segment along the y-axis from the graph of f(x) down to the x-axis.

  • How is the length of the curve between the points on the graph of f(x) found?

    -The length of the curve between the points on the graph of f(x) is found by integrating the arc length formula with respect to x from 0 to k.

  • What is the total length of the two vertical line segments in the perimeter of R?

    -The total length of the two vertical line segments in the perimeter of R is 2k.

Outlines
00:00
📐 Calculating the Perimeter of a Region with an Integral

This paragraph discusses the process of finding the perimeter of a region R in the first quadrant, defined by the graph of the function f(x) = e^(2x), the coordinate axes, and the vertical line x = k. The focus is on part a of a problem, which asks for an expression involving an integral that gives the perimeter in terms of k without evaluating it. The explanation involves rederiving the arc length formula using calculus, specifically focusing on the derivative of the function and applying the Pythagorean theorem to small segments of the curve to approximate the arc length. The integral expression derived is ∫ from 0 to k of the square root of 1 + (f'(x))^2 dx, with f'(x) = 2e^(2x).

05:01
📐 Completing the Perimeter Calculation

This paragraph continues from the previous one, focusing on completing the calculation for the perimeter of region R. After deriving the integral expression for the arc length, the remaining parts of the perimeter are addressed. The segment along the function from x=0 to x=k is considered, as well as the lengths along the x-axis and the vertical line, which are straightforward to calculate. The final expression for the perimeter includes these lengths plus the previously derived integral, resulting in a complete expression for the perimeter in terms of k, although it is not evaluated.

Mindmap
Keywords
💡Perimeter
Perimeter refers to the total length around a two-dimensional shape. In the context of the video, it is used to describe the combined length of the sides of the region R, which is bounded by the graph of the function f(x) = e^(2x), the coordinate axes, and the vertical line x = k. The video aims to derive an expression for the perimeter of R in terms of k without evaluating it, which is a key part of understanding the problem.
💡Integral
An integral is a mathematical concept used to calculate the area under a curve or the accumulation of a quantity over an interval. In the video, the integral is used to find the arc length of the curve defined by the function f(x) = e^(2x) from x = 0 to x = k, which is a part of the perimeter calculation for the region R.
💡Arc Length
Arc length is the distance around a curve. In the video, the arc length is a critical component of the perimeter of the region R, which lies in the first quadrant and is bounded by the curve defined by the function f(x) and the coordinate axes. The video explains how to derive the arc length formula for a curve using calculus, which involves taking into account the derivative of the function and applying the Pythagorean theorem to small segments of the curve.
💡Derivative
A derivative in calculus represents the rate of change of a function with respect to its variable. It is used to find the slope of the tangent line at any point on the curve defined by the function. In the video, the derivative of f(x) = e^(2x), denoted as f'(x), is calculated to determine the rate of change of the curve and to help derive the arc length formula.
💡First Quadrant
The first quadrant is the top-right section of the Cartesian coordinate system where both x and y coordinates are positive. The video discusses a region R that lies entirely within the first quadrant and is bounded by the graph of the function f(x), the x-axis, the y-axis, and the vertical line x = k.
💡Coordinate Axes
Coordinate axes are the lines that intersect at the origin (0,0) of a Cartesian coordinate system and along which the points are plotted. In the video, the coordinate axes define the boundaries of the region R, with the x-axis and y-axis serving as two of the sides of the shape.
💡Vertical Line
A vertical line is a line that runs perpendicular to the horizontal axis (x-axis) in a Cartesian coordinate system. In the video, the vertical line x = k is one of the boundaries of the region R, helping to define its shape and limits in the first quadrant.
💡e to the 2x
e to the 2x is an exponential function where e is the base of the natural logarithm, approximately equal to 2.71828, and the variable x is the exponent. This function represents the curve that the region R is bounded by in the first quadrant. The function has a specific derivative that is used in the calculation of the arc length and the perimeter of R.
💡Pythagorean Theorem
The Pythagorean theorem is a fundamental principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In the video, the theorem is used to approximate the arc length of the curve by considering small segments of the curve as right-angled triangles.
💡Parametric Definition
A parametric definition is a way to describe a curve by giving the coordinates of points on the curve as functions of a parameter. Although the video does not deal with a function defined parametrically, it mentions this concept as a comparison to the non-parametric approach used for the function f(x) = e^(2x).
💡Summation
Summation is the process of adding together a sequence of numbers or terms. In the video, the summation concept is used to think of the integral as the sum of infinitesimally small segments of the arc length, which is an application of the fundamental theorem of calculus.
Highlights

The problem involves finding the perimeter of a region R in the first quadrant.

The function f(x) is given as f(x) = e^(2x).

Region R is bounded by the graph of f(x), the coordinate axes, and the vertical line x = k.

The perimeter of R is composed of the length of the curve, the vertical line, and the horizontal line.

The arc length formula is rederived using calculus, emphasizing understanding for practical applications.

A small change in x is denoted as dx, and the corresponding change in y is denoted as dy.

The derivative of y with respect to x (dy/dx) is equal to f'(x), which is 2e^(2x) for the given function.

The arc length is approximated using the Pythagorean theorem for small changes in x and y.

The expression for small arc length is the square root of (dx^2) + (f'(x)^2 * dx^2).

The integral expression for the arc length is derived as ∫ from 0 to k of the square root of (1 + (4e^(4x))) dx.

The perimeter of R includes the length of the curve, a segment of length 1, and lengths k and e^(2k) along the axes.

The integral expression for the perimeter does not need to be evaluated to complete the problem.

The problem showcases the application of calculus in determining the perimeter of a region bounded by a curve and lines.

The problem emphasizes the importance of understanding the derivation of formulas for practical use and not just memorization.

The problem tests the understanding of the relationship between the derivative and the rate of change.

The problem illustrates the use of the Pythagorean theorem in calculating arc length.

The problem requires the integration of calculus concepts to find the perimeter of a shape defined by a function.

Transcripts

Browse More Related Video

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

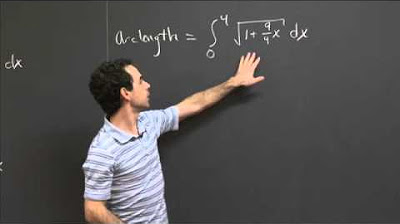
Arc Length of y=x^(3/2) | MIT 18.01SC Single Variable Calculus, Fall 2010

2017 AP Calculus AB Free Response #6

AP Calculus AB Crash Course Day 8 - Integration and Riemann Sums

How long is a curve?? The Arclength Formula in 3D

2021 AP Calculus AB Free Response #1 Solutions (First Administration)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusArc LengthPerimeterIntegrationDerivativesFirst Quadrante^(2x)AP ExamEducation