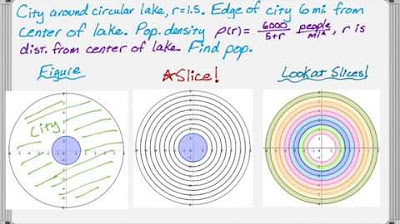
2021 AP Calculus AB Free Response #1 Solutions (First Administration)
TLDRThe video script discusses a calculus problem involving the density of a bacteria population in a circular petri dish. The density function f(r) is given in milligrams per square centimeter, with selected values provided in a table. The video demonstrates how to estimate the derivative f'(22.25) using a secant line approximation, resulting in a rate of increase of eight milligrams per cubic centimeter. It then calculates the total mass of bacteria in the petri dish using the integral expression 2π∫₀^₄r*f(r)dr, which is approximated through a right Riemann sum, yielding an overestimate due to the increasing nature of the function r*f(r). The units of the total mass are determined by the integration process, resulting in milligrams. Lastly, the script explores finding the value of k for which the function g(r) equals the average value of g(r) over an interval, which is solved graphically, with the intersection occurring at k ≈ 2.497 centimeters.
Takeaways
- 📊 The script discusses the use of calculus to estimate the density of bacteria in a circular petri dish, with the density function f(r) given in milligrams per square centimeter.
- 🔍 To estimate the derivative f'(r) at a specific point, the speaker uses a secant line approximation between two data points, demonstrating the calculation for f'(2.25).
- 🧮 The units of the derivative are calculated by the speaker, resulting in milligrams per cubic centimeter, which represents the rate of increase of bacterial density with respect to radius.
- 🌀 The total mass of bacteria in the petri dish is approximated using the integral of 2π times the product of r and f(r) from 0 to 4, with the integral calculated as a Riemann sum.
- 🔢 The speaker leaves the final result of the integral in terms of π for simplicity, but calculates the numerical sum to be approximately 845.08 milligrams.
- 📈 The approximation from part b is identified as an overestimate of the total mass of bacteria due to the nature of the increasing function and the use of a right Riemann sum.
- 📐 The script explores modeling the bacterial density with a function g(r) and finding the value of k for which g(k) equals the average value of g(r) over an interval.
- 💡 The average value is determined by dividing the integral of g(r) over the interval by the length of the interval, which is 3 in this case.
- ✅ The speaker uses a graphing method to find the intersection of g(k) with the average value, which occurs at k ≈ 2.497 centimeters.
- 🤔 The speaker emphasizes the importance of understanding the concept of 'rate' in the context of the problem, clarifying that it refers to the rate of change of density per radius, not per time.
- 📋 The process involves several mathematical steps, including calculating derivatives, integrals, and Riemann sums, which are all explained in a step-by-step manner.
Q & A
What is the context of the calculus problem discussed in the transcript?
-The context is a calculus problem involving the density of a bacteria population in a circular petri dish, where the density is given by a differentiable function f(r) measured in milligrams per square centimeter.
How is the density function f(r) represented in the problem?
-The density function f(r) is represented by selected values in a table, and the problem involves using these values to estimate the derivative f'(r) at a specific point.
What method is used to estimate the derivative f'(22.25) in the transcript?
-The method used to estimate the derivative f'(22.25) is by approximating it with a secant line slope using the values of f at two points, f(2.5) and f(2).
What is the unit of the estimated derivative f'(22.25)?
-The unit of the estimated derivative f'(22.25) is milligrams per cubic centimeter, which represents the rate of increase of the bacteria density with respect to the radius.
How is the total mass of bacteria in the petri dish calculated?
-The total mass of bacteria in the petri dish is calculated using the integral expression 2π∫₀⁴r*f(r) dr, which is approximated using a Riemann sum with specific intervals and the given values from the table.
What is the significance of the units in the integral calculation for the total mass?
-The significance of the units in the integral calculation is that they show the conversion from milligrams per square centimeter (the units of f(r)) to milligrams (the final unit for the total mass), as the square centimeter units cancel out.
Why is the approximation found in part (b) considered an overestimate?
-The approximation is considered an overestimate because a right Riemann sum is used, and since the function r*f(r) is increasing, the larger values of the intervals are chosen, leading to an overestimation of the total mass.
What is the purpose of finding the average value of the function g(r) over an interval in the problem?
-The purpose is to determine the value of k for which g(k) equals the average value of g(r) over the interval, which can be found by setting the integral of g(r) over the interval equal to g(k) and solving for k.
How is the average value of g(r) over the interval calculated?
-The average value is calculated by dividing the integral of g(r) from 1 to 4 by the length of the interval, which is 3 in this case.
What mathematical tool is used to find the value of k where g(k) equals the average value?
-Graphing is used as a tool to find the value of k where g(k) equals the average value by plotting both g(r) and the average value function and finding their intersection.
What is the approximate value of k found in the transcript?
-The approximate value of k found in the transcript is 2.497 centimeters.
How does the speaker ensure the accuracy of the average value calculation?
-The speaker ensures the accuracy by graphing the functions to visually confirm that the calculated average value seems reasonable and by performing calculations step by step, double-checking the mathematical process.
Outlines
Calculus Problem: Bacteria Density Estimation 📊
The first paragraph introduces a calculus problem involving the estimation of the density of a bacteria population in a circular petri dish. The density is given by a differentiable function f(r), with values provided in a table. The task is to estimate the derivative f'(22.25) using a secant line approximation between two given points. The units of the derivative are calculated, and the interpretation of the rate of increase in bacterial density is discussed. Additionally, the total mass of bacteria in the petri dish is approximated using an integral expression, and the method of calculating the Riemann sum for this purpose is explained. The paragraph concludes with a discussion on the units of the calculated total mass.
Analysis of Bacterial Mass Approximation and Function Modeling 📈
The second paragraph delves into whether the approximation found in the previous calculation overestimates or underestimates the total mass of bacteria in the petri dish. It is determined that since the function is increasing, the right Riemann sum used will likely overestimate the actual mass. The paragraph then models the density of bacteria using a function g(r) and seeks to find the value of k for which g(k) equals the average value of g(r) over a given interval. The average value is calculated by dividing the integral of the function over the interval by the length of the interval. The integral is solved, and the resulting average value is used to find the value of k where g(k) equals this average. The process involves graphing the function and its average to find the point of intersection, which is approximated to be at k equals 2.497 centimeters.
Mindmap
Keywords
💡Calculus
💡Secant Line
💡Derivative
💡Integral
💡Riemann Sum
💡Units of Measurement
💡Rate of Increase
💡Average Value
💡Modeling
💡Graphing
💡Correction
Highlights
The density of bacteria population in a circular petri dish is given by an increasing differentiable function f(r), measured in milligrams per square centimeter.
Estimation of f'(22.25) is done using a secant line slope between two points, f(2.5) - f(2) / (2.5 - 2).
The units of the rate of increase in density are milligrams per cubic centimeter, representing the change in density per centimeter squared.
The total mass of bacteria in the petri dish is approximated using the integral expression 2π∫₀⁴r*f(r)dr.
The integral is approximated by creating entries for r*f(r) from the given data table.
The Riemann sum is calculated using the right endpoint method, which may overestimate the total mass due to the increasing nature of r*f(r).
The average value of g(r) over the interval is found by dividing the integral of g(r)dr from 1 to 4 by the interval width.
The function g(r) is defined as g(r) = 2 - 16cos(1.57√r), and its integral is calculated from 1 to 4.
The average value of g(r) is approximately 9.876, which is used to find the value of k where g(k) equals this average.
Graphical method is used to approximate the intersection of g(r) and the average value, resulting in k ≈ 2.497 cm.
The rate of increase in bacterial density per radius is discussed, highlighting the interpretation of the derivative in a biological context.
The importance of specifying units when performing calculus operations to ensure the physical meaning of results is emphasized.
The use of a calculator for precise calculation of the derivative is mentioned, indicating a practical approach to solving the problem.
The concept of a Riemann sum in approximating the total mass of bacteria is explained, showcasing an essential mathematical technique.
The potential for overestimation in the Riemann sum due to the function's increasing nature is pointed out, demonstrating an understanding of the method's limitations.
The process of setting up and solving the integral to find the average value of g(r) is detailed, illustrating a step-by-step approach to calculus problems.
The choice of a graphical method to find the intersection point is justified, showing an alternative to algebraic solutions in certain scenarios.
The final answer for the value of k is presented with an approximation, reflecting a practical approach to finding a solution that meets the problem's requirements.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: