Arc Length of y=x^(3/2) | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare
7 Jan 201107:03
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter guides viewers through calculating the arc length of a curve defined by y = x^(3/2). The focus is on the curve segment between x = 0 and x = 4. The presenter explains the formula for arc length, ds, and how to apply it to the given function by finding dy/dx and integrating from the given bounds. A substitution method simplifies the integral, leading to a solvable expression. The video concludes with an approximate numerical estimation of the arc length, demonstrating the application of calculus to real-world problems.

Takeaways
  • 📚 The video is focused on computing the arc length of a curve defined by the equation y = x^(3/2).
  • 🔍 The curve is sketched and the segment of interest is between x = 0 and x = 4.
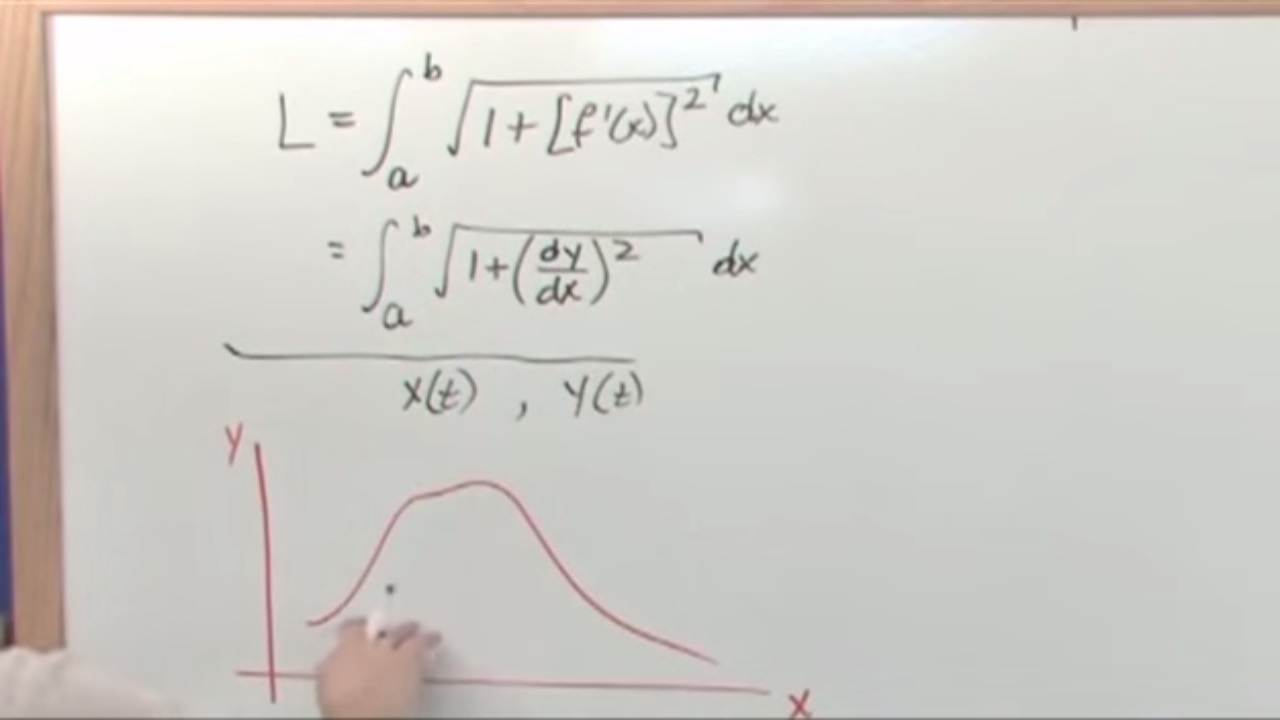
  • 📈 The formula for arc length, ds, is derived from the Pythagorean theorem as √(dx^2 + dy^2).
  • 📘 An alternative formula for ds is √(1 + (dy/dx)^2)dx, which is used for integration.
  • 📝 The derivative of y with respect to x, dy/dx, is calculated as (3/2)√x.
  • 🔑 The expression for ds is simplified to √(1 + (9/4)x^2)dx by substituting the derivative.
  • 📉 The integral for the arc length is set up from 0 to 4 using the simplified expression for ds.
  • 🔄 A substitution method is introduced with u = 1 + (9/4)x to simplify the integral.
  • 📌 The new integral bounds are adjusted from 1 to 10 corresponding to the original x bounds.
  • 📊 The integral is evaluated to find the arc length, resulting in a closed-form expression.
  • 🔢 The final arc length is approximated numerically, with an estimate provided for the decimal value.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is computing the arc length of a curve given by the equation y = x^(3/2).

  • What is the range of x values for which the arc length of the curve is being calculated?

    -The arc length is being calculated for the range of x values from 0 to 4.

  • What is the formula for the differential arc length ds in terms of dx and dy?

    -The formula for the differential arc length ds is √(dx^2 + dy^2).

  • How can the formula for ds be rewritten in terms of dy/dx?

    -The formula for ds can be rewritten as √(1 + (dy/dx)^2) dx.

  • What is the derivative of y with respect to x when y = x^(3/2)?

    -The derivative of y with respect to x, denoted as dy/dx, is (3/2) * x^(1/2) or (3/2) * √x.

  • What substitution is made to simplify the integral for the arc length?

    -The substitution made is u = 1 + (9/4)x, with du = (9/4)dx, and dx = (4/9)du.

  • What are the new bounds for the integral after the substitution?

    -The new bounds for the integral are from u = 1 to u = 10.

  • What is the integral expression for the arc length after the substitution?

    -The integral expression for the arc length after the substitution is ∫(4/9)√u du from 1 to 10.

  • How is the integral of √u evaluated?

    -The integral of √u is evaluated as (2/3)u^(3/2), and after multiplying by the constant (4/9), it becomes (8/27)u^(3/2).

  • What is the final expression for the arc length after evaluating the integral?

    -The final expression for the arc length is (8/27)[10^(3/2) - 1^(3/2)] which simplifies to (8/27)(10^(3/2) - 1).

  • How does the video suggest estimating the arc length without a calculator?

    -The video suggests estimating the arc length by recognizing that √10 is slightly more than 3, and thus the result is likely a bit larger than 8.

Outlines
00:00
📚 Introduction to Arc Length Problem

The video script begins with an introduction to a problem-solving session focused on computing the arc length of a specific curve. The curve in question is defined by the equation y = x^(3/2), and the instructor provides a sketch to visualize its shape. The task is to calculate the arc length of the curve between x = 0 and x = 4. The audience is encouraged to pause the video and attempt the calculation before continuing. Upon returning, the instructor starts by explaining the concept of arc length and the formula for a small piece of arc length, ds, which is derived from the Pythagorean theorem and can be expressed as ds = sqrt(1 + (dy/dx)^2)dx. The function y in terms of x is then differentiated to find dy/dx, resulting in 3/2 * sqrt(x), which is substituted back into the arc length formula to prepare for integration.

05:01
🔍 Detailed Calculation of Arc Length

The second paragraph delves into the detailed calculation of the arc length. The instructor uses a substitution method to simplify the integral, setting u = 1 + (9/4)x, which leads to du = (9/4)dx and dx = (4/9)du. The bounds for u are also adjusted according to the original x bounds, resulting in an integral from u = 1 to u = 10. The integral simplifies to a form that can be easily computed by hand, and the instructor guides the audience through the integration process, resulting in an expression involving u to the power of 3/2. After evaluating the integral, the instructor provides a rough estimate of the arc length in decimal form and encourages the audience to use a calculator for a more precise value. The summary concludes by emphasizing the straightforward application of the formulas for arc length and the successful evaluation of the integral in closed form.

Mindmap
Keywords
💡Arc Length
Arc length is the measure of the distance along a curve between two points. In the video, the concept is central to the problem-solving process, as the host guides the viewers through the computation of the arc length of a specific curve. The script uses the formula for arc length, \( ds = \sqrt{dx^2 + dy^2} \), to derive the integral that will give the length of the curve y = x^(3/2) between x = 0 and x = 4.
💡Curve
A curve in mathematics refers to a continuous and smooth path, which can be represented by a function. In the script, the curve is given by the equation y = x^(3/2), and the host is interested in calculating the arc length of a segment of this curve. The curve is described as curving upwards but not as fast as a parabola, providing a visual context for the problem.
💡Integral
An integral in calculus represents the process of summing up all the infinitesimally small elements of a function to find a total quantity, such as the area under a curve. In the context of the video, the integral is used to find the arc length of the curve by integrating the differential arc length, \( ds \), over the interval [0, 4].
💡Differential Arc Length
The differential arc length, represented as \( ds \), is a small segment of the curve that can be approximated as a straight line. The script explains that \( ds \) can be found using the Pythagorean theorem in the context of calculus, and it is a key component in setting up the integral for arc length calculation.
💡Derivative
A derivative in calculus gives the rate at which a function changes with respect to its variable. In the script, the derivative of y with respect to x, \( dy/dx \), is calculated as \( \frac{3}{2}x^{1/2} \) or \( \frac{3}{2}\sqrt{x} \), which is necessary for finding the differential arc length of the curve.
💡Substitution
Substitution is a common technique in calculus used to simplify integrals by replacing a variable with another expression. In the video, the host uses the substitution \( u = 1 + \frac{9}{4}x \) to transform the integral of the square root of \( 1 + \frac{9}{4}x \) into a more manageable form, making it easier to evaluate.
💡Bounds of Integration
Bounds of integration specify the limits within which an integral is evaluated. In the script, the bounds for the integral that calculates the arc length are given as x = 0 and x = 4, which are later transformed to u = 1 and u = 10 after the substitution.
💡Square Root
The square root operation finds a value that, when multiplied by itself, gives the original number. In the context of the video, the square root is used in the expression for the differential arc length and in the integral's integrand, \( \sqrt{1 + \frac{9}{4}x} \), which is crucial for the arc length calculation.
💡Polynomial
A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, and multiplication, and non-negative integer exponents. The script mentions that most polynomials would result in difficult integrals for arc length, but the specific polynomial given, \( x^{3/2} \), allows for an integrable expression.
💡Numerical Method
Numerical methods are techniques used to find approximate solutions to mathematical problems that cannot be solved exactly. The host mentions that for most polynomials, computing arc length would require numerical methods, but the chosen curve allows for an exact solution without the need for such approximations.
Highlights

Introduction to computing the arc length of a curve defined by y = x^(3/2).

Sketch of the curve and focus on the segment between x = 0 and x = 4.

Recall the formula for arc length ds using the Pythagorean theorem analogy.

Alternative formula for ds involving dy/dx for integration purposes.

Derivation of dy/dx for the given curve y = x^(3/2).

Substitution of dy/dx into the arc length formula to find ds.

Integration of ds from x = 0 to x = 4 to find the arc length.

Use of substitution method to simplify the integral calculation.

Setting up the substitution with u = 1 + (9/4)x and du = (9/4)dx.

Adjusting the bounds of integration from x to u.

Simplified integral calculation using the substitution method.

Integration result expressed as a function of u.

Final calculation of the arc length using the evaluated integral.

Estimation of the arc length result without a calculator.

Discussion on the rarity of being able to compute arc lengths by hand.

Conclusion emphasizing the application of standard arc length formulas.

Transcripts

Browse More Related Video

Finding Arc Length Using an Integral

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

AP Calculus BC Lesson 8.13

Arc Length Calculus Problems,

Area Between Curves: Integrating with Respect to y (Example 1)

2011 Calculus BC free response #3a | AP Calculus BC | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Arc LengthMath TutorialCurve AnalysisIntegral CalculusDerivativeSubstitution MethodEducational ContentMathematics EducationProblem SolvingGeometryTrigonometry