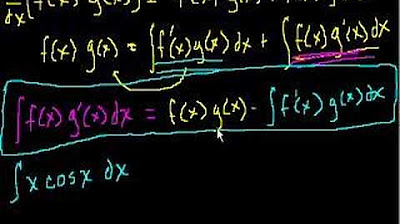Integration by Parts (part 6 of Indefinite Integration)

Khan Academy
21 Oct 200709:34
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a detailed walkthrough of the integration by parts technique, emphasizing its application for complex integrals. The presenter illustrates the process with the integral of x squared times e to the x, highlighting the importance of recognizing when to use this method. The example demonstrates the derivation from the product rule of differentiation and the iterative application of integration by parts to simplify and solve the integral, ultimately yielding a solvable expression. The video aims to equip viewers with the knowledge and confidence to tackle challenging integral problems using integration by parts as a valuable tool in their mathematical toolkit.

Takeaways
  • 📝 Integration by parts is a technique used for integrating products of functions, and it's based on the product rule of differentiation.
  • 🤔 It's helpful to memorize the integration by parts formula, but if forgotten, it can be derived from the product rule of differentiation.
  • 🎨 Integration by parts requires recognizing when to use it, often as a last resort when other methods like substitution or reverse chain rule are not applicable.
  • 🌟 The key to integration by parts lies in choosing the correct u and dv (functions and their derivatives) to simplify the integration process.
  • 📚 The formula for integration by parts is symmetric, which makes it easier to remember: ∫u dv = uv - ∫v du.
  • 🔄 In the example given, x^2 * e^x is integrated by choosing x^2 as u and e^x as dv, leading to a simpler integral to solve.
  • 🔢 When applying integration by parts, the antiderivative of e^x is e^x, which simplifies the process, and the derivative of x^n is nx^(n-1).
  • 💡 Integration by parts can be used iteratively, as shown in the example, to further simplify the integral until it's easily solvable.
  • 🎓 The process of integration by parts might be tedious, but it's a powerful tool in solving complex integrals, reducing the exponent on the x-term with each iteration.
  • 📈 The video script serves as a guide on how to approach and tackle difficult integration problems using integration by parts.
Q & A

  • What is the formula for integration by parts?

    -The formula for integration by parts is ∫u dv = uv - ∫v du, where u and v are functions of x, du is the derivative of u with respect to x, and dv is the derivative of v with respect to x.

  • Why is it important to remember the integration by parts formula?

    -Remembering the integration by parts formula is important because it is a powerful tool for integrating products of functions, especially when other integration techniques like substitution or simplification are not applicable.

  • How does one decide when to use integration by parts?

    -Integration by parts is often used as a last resort when other integration techniques fail. It is particularly useful when the integrand involves a product of functions where one function is a trigonometric function or an exponential function, and the other cannot be easily integrated by other methods.

  • What is the role of the product rule in integration by parts?

    -Integration by parts is essentially the reverse of the product rule in differentiation. The product rule states that (f * g)' = f' * g + f * g', and integration by parts uses this relationship to break down the integral of a product of functions into simpler components.

  • How does the讲师 (lecturer) choose the functions u and dv in integration by parts?

    -The lecturer chooses the functions u and dv strategically to simplify the integration process. Generally, u is chosen to be the function that can be easily differentiated, and dv is chosen to be the function that becomes simpler when integrated.

  • What was the first integral problem presented in the script?

    -The first integral problem presented was ∫x^2 * e^x dx.

  • How did the lecturer determine the functions u and dv for the integral ∫x^2 * e^x dx?

    -The lecturer determined that u should be x^2 because its derivative simplifies to a constant (2x), and dv should be e^x because its integral is the same function (e^x), which does not complicate the process further.

  • What was the result of the first integration by parts in the script?

    -After the first integration by parts, the lecturer obtained the result x^2 * e^x - ∫2x * e^x dx.

  • How did the lecturer handle the remaining integral ∫2x * e^x dx after the first integration by parts?

    -The lecturer applied integration by parts again to the remaining integral ∫2x * e^x dx, choosing u to be 2x (which simplifies to 2 when differentiated) and dv to be e^x (which integrates to e^x).

  • What is the final result of the indefinite integral of x^2 * e^x?

    -The final result of the indefinite integral of x^2 * e^x is x^2 * e^x - 2x * e^x + 2 * e^x + C, where C is the constant of integration.

  • What does the lecturer suggest about solving more complex integrals involving x^n * e^x?

    -The lecturer suggests that with practice and application of integration by parts, even more complex integrals like x^n * e^x can be tackled. The process may be tedious, but each iteration of integration by parts reduces the exponent on the x-term, eventually leading to a manageable integral.

Outlines
00:00
📚 Introduction to Integration by Parts

The paragraph begins with an introduction to the concept of integration by parts, emphasizing its utility in solving complex integration problems within a limited time frame. The speaker explains the formula for integration by parts, highlighting its derivation from the product rule of differentiation. The importance of recognizing when to apply this method is stressed, with the speaker sharing personal strategies for identifying its applicability, such as the presence of exponential or trigonometric functions. The paragraph culminates with the speaker posing a problem involving the integration of x squared times e to the power of x, illustrating the process of selecting appropriate functions for f(x) and g'(x) to simplify the integral.

05:03
🔍 Applying Integration by Parts to a Complex Example

This paragraph delves into the application of integration by parts to a more complex example, specifically the integral of x squared times e to the x. The speaker guides the audience through the process of identifying the functions f(x) and g'(x), emphasizing the importance of simplifying the derivative and the antiderivative. The explanation continues with the execution of integration by parts, including the calculation of intermediate steps and the final simplification of the integral. The speaker also discusses the potential for applying integration by parts repeatedly to further simplify the problem. The paragraph concludes with the speaker reflecting on the usefulness of integration by parts for tackling a variety of integration problems and the intention to cover more examples in future presentations.

Mindmap
Keywords
💡Integration by Parts
Integration by Parts is a technique used in calculus to evaluate integrals by converting the given integral into a more manageable form. It is based on the product rule of differentiation, effectively reversing the process. In the video, the presenter uses Integration by Parts as a strategy to tackle complex integrals, such as those involving exponential functions and polynomials. The method involves identifying two functions within the integral, one of which is integrated while the other's derivative is taken, with the process repeated until a simpler form is achieved.
💡Product Rule
The Product Rule is a fundamental principle in calculus that describes how to differentiate a product of two functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the context of the video, the Product Rule is related to Integration by Parts as the latter is essentially the reverse of the former. The presenter refers to the Product Rule to help remember and derive the Integration by Parts formula.
💡Derivative
A derivative in calculus represents the rate of change or the slope of a function at a particular point. It is a fundamental concept used to analyze the behavior of functions. In the video, the derivative is a key component in the process of Integration by Parts, where the derivative of one function is taken while the integral of another is computed. The presenter discusses choosing functions for Integration by Parts based on which function's derivative simplifies the process.
💡Antiderivivative
An antiderivative, also known as an indefinite integral, is a function whose derivative is the given function being integrated. It is the reverse process of differentiation. In the video, finding the antiderivative is the ultimate goal of integration problems, including those solved using Integration by Parts. The presenter emphasizes that the antiderivative of e^x is e^x, which is a key insight used in the example provided.
💡Chain Rule
The Chain Rule is a method in calculus used to differentiate composite functions. It involves differentiating the outer function first and then multiplying by the derivative of the inner function. In the video, the Chain Rule is mentioned as a technique to simplify complex derivatives before applying Integration by Parts. The presenter suggests using the Chain Rule to identify which part of the integral to differentiate or integrate first for simplification.
💡e to the x (e^x)
e^x, where e is the base of the natural logarithm, is a common exponential function in calculus. It has unique properties, such as its own derivative being the function itself and its antiderivative also being e^x. In the video, the function e^x is a part of the integral that the presenter is solving using Integration by Parts, highlighting its simplicity in both differentiation and integration processes.
💡Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, are mathematical functions that relate angles to real numbers. They are often used in solving problems involving periodic phenomena. In the video, the presenter mentions trigonometric functions as a type of function that, when encountered in an integral, might prompt the use of Integration by Parts if other methods like substitution are not applicable.
💡Complex Integrals
Complex integrals refer to integrals that are difficult to solve using basic integration techniques. They often involve functions that are not easily integrable, such as those with complex derivatives or those that do not fit standard integration formulas. In the video, the presenter focuses on tackling complex integrals using Integration by Parts, demonstrating how to break down and simplify challenging integrals into more manageable forms.
💡Practice
Practice in the context of the video refers to the repetitive application of mathematical techniques to solve problems, specifically in calculus. It is through practice that one becomes proficient in recognizing patterns, applying rules, and solving complex integrals. The presenter emphasizes the importance of practice in mastering Integration by Parts and other calculus concepts.
💡Solvable Integral
A solvable integral is an integral for which a solution exists and can be found using various integration techniques. In the context of the video, the presenter assumes that any integral presented in an exam is solvable, and if other methods fail, Integration by Parts is a viable last resort. The concept reinforces the idea that all integrals encountered in typical mathematical problems have solutions, even if they require advanced techniques to solve.
💡Color Coding
Color coding in the video serves as a visual tool to differentiate between various components of the integration process. It helps to distinguish between functions, their derivatives, and the results of operations, making the complex process of Integration by Parts more understandable and less confusing. The presenter uses color coding to keep track of the functions and their corresponding derivatives and antiderivatives throughout the example.
Highlights

Integration by parts is an essential technique for solving complex integrals, especially when other methods like substitution or reverse chain rule are not applicable.

The formula for integration by parts is derived from the product rule of differentiation, and it can be memorized due to its symmetry.

Integration by parts is more of an art than a systematic process, and it requires practice to recognize when to use it effectively.

The key to using integration by parts is selecting the appropriate functions for f(x) and g'(x) to simplify the integral and make it easier to solve.

In the example provided, x^2e^x is chosen as the integral to be solved using integration by parts, with x^2 as f(x) and e^x as g'(x), due to their derivatives and antiderivatives' simplicity.

The process of integration by parts may involve nested applications, where integration by parts is applied within the solution of the original problem.

The final result of the integral of x^2e^x is a combination of terms that have been simplified through the application of integration by parts, showcasing the power of this method.

Integration by parts can be applied repeatedly to tackle increasingly complex integrals, reducing the complexity of the x-term with each application.

The video aims to demystify the concept of integration by parts and encourages practice to gain comfort and proficiency with the method.

The presenter emphasizes the importance of recognizing when an integral is solvable and encourages the use of integration by parts as a last resort technique on exams.

The example provided illustrates the selection process for f(x) and g'(x) in integration by parts, highlighting the thought process behind choosing functions that simplify the integral.

The video demonstrates the application of integration by parts through a step-by-step walkthrough of a specific integral, providing clarity on how to approach and solve the problem.

The presenter's approach to solving integrals involves a strategic selection of integration techniques based on the characteristics of the integral, showcasing a problem-solving strategy.

The video serves as a tutorial on the application of integration by parts, providing insights into the method's process and its usefulness in solving a variety of integral problems.

The integration by parts method is introduced as a valuable tool in a mathematician's toolkit, capable of tackling a wide range of integral problems.

The video emphasizes the importance of practice and familiarity with integration by parts to efficiently tackle complex integrals.

Transcripts

Browse More Related Video

integration by parts, DI method, VERY EASY

4.6 - Integration Techniques - Integration by Parts

Integration by parts: ºx____dx | AP Calculus BC | Khan Academy

Indefinite Integration (part V)

Calculus - Integration By Parts

Integration by Parts... How? (NancyPi)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusIntegrationProduct RuleDerivativesAntiderivativese^x FunctionEducational ContentProblem SolvingOnline Tutorial