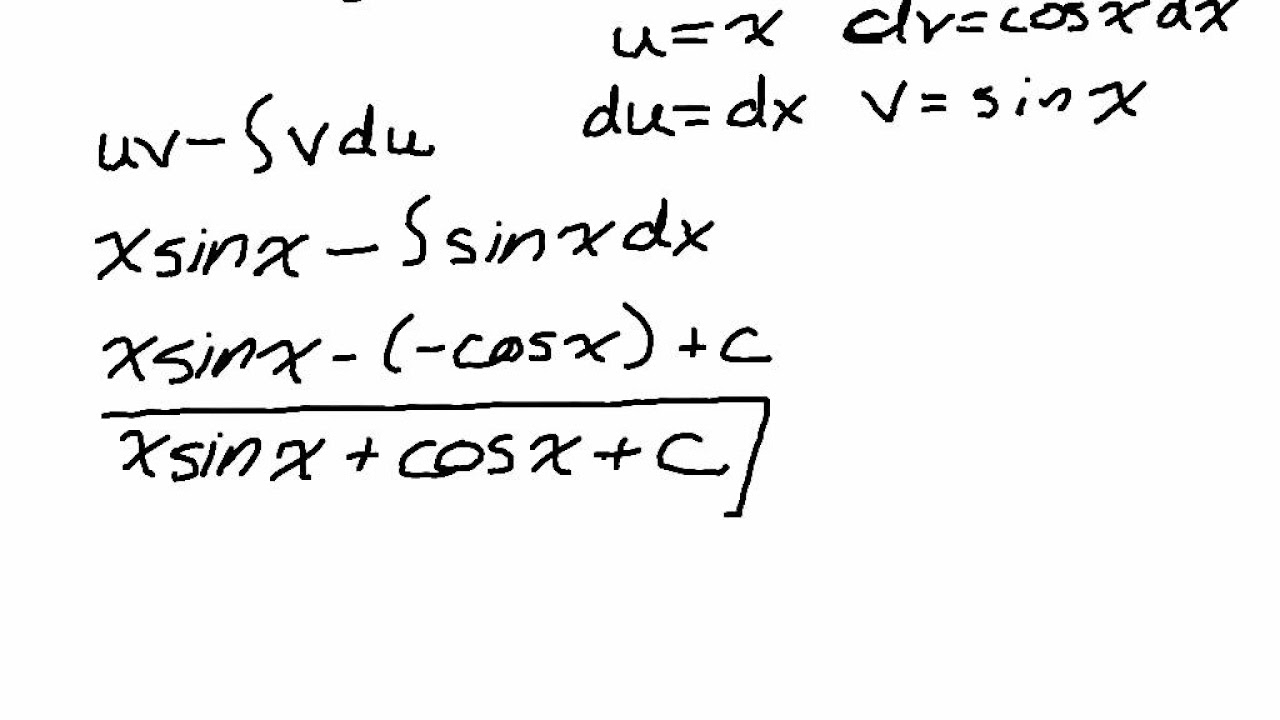Integration by Parts... How? (NancyPi)
TLDRIn this informative video, Nancy teaches the concept of integration by parts, a technique used to simplify complex integrals. She explains the process step by step, emphasizing the importance of choosing the correct u and dv for the formula. Nancy introduces the LIATE acronym as a helpful trick for selecting u and dv and demonstrates the method using the integral of x times e^x as an example. She assures viewers that with practice, they will become more adept at applying integration by parts, even for more complicated cases.
Takeaways
- 📚 Integration by parts is a technique used to integrate products of two functions that are more challenging to integrate directly.
- 🤔 Before applying integration by parts, check if the integral can be simplified or if substitution is a viable alternative.
- 🔄 The integration by parts formula rewrites the integral of a product into a new integral that is hopefully easier to compute.
- 🎯 To apply integration by parts, choose u and dv carefully, with u being the function that simplifies upon differentiation.
- 📈 The derivative of u (du) and the integral of dv (v) are essential components in applying the integration by parts formula.
- 🔢 The LIATE acronym (Log, Inverse Trig, Algebraic, Trig, Exponential) is a helpful tool for selecting u in integration by parts.
- 📊 When using the LIATE rule, prioritize the function that appears first in the acronym if it's present in the integrand.
- 🔄 For products involving both exponential and trigonometric functions (E and T), either can be chosen as u since they're interchangeable.
- 🌟 Practice is key in becoming proficient at choosing u and dv, and don't be discouraged if the first attempt doesn't work out.
- 📝 Remember to include the constant of integration (+c) when solving indefinite integrals using integration by parts.
Q & A
What is integration by parts and why is it used?
-Integration by parts is a technique used in calculus to integrate a product of two functions. It is used when the direct integration of a product is difficult or not possible using basic integration rules.
How does one decide which function to use as u and which as dv in integration by parts?
-A general rule of thumb is to choose u as the function that simplifies (becomes simpler) upon differentiation and dv as the other function. This typically means the function that reduces in complexity, such as a lower order or fewer terms after differentiation.
What is the LIATE acronym mentioned in the script, and how does it help with integration by parts?
-The LIATE acronym is a mnemonic device to help remember the order in which to consider functions when choosing u and dv for integration by parts. It stands for Log, Inverse Trig, Algebraic, Trig, and Exponential. The first function in this sequence that appears in the integrand is chosen as u, and the rest of the integrand becomes dv.
What happens if the choice of u and dv does not simplify the integration?
-If the initial choice of u and dv does not simplify the integration, it's possible to try a different combination. The process may require multiple attempts and a better understanding of the functions involved to make an informed choice.
What are the steps involved in performing integration by parts?
-The steps are: 1) Choose u and dv according to the LIATE rule or general guideline. 2) Differentiate u to find du. 3) Integrate dv to find v. 4) Apply the integration by parts formula: ∫u dv = uv - ∫v du + C, where C is the constant of integration.
How does the integration by parts formula look?
-The integration by parts formula is given by: ∫u dv = uv - ∫v du + C. Here, u and v are the functions chosen from the integrand, du is the derivative of u, and dv is the integral of the other function in the product.
What should be considered when integrating a product of two functions that involves trigonometric and exponential functions?
-When dealing with a product of trigonometric and exponential functions, either can be chosen as u or dv since they are interchangeable according to the LIATE rule. However, the process may require performing integration by parts multiple times to reach a solvable form.
Can integration by parts be applied to definite integrals?
-Yes, integration by parts can be applied to definite integrals. However, it requires evaluating the limits of integration for each term in the formula, making the process slightly more complex.
What is the significance of the constant of integration (C) in indefinite integrals?
-The constant of integration (C) is necessary in indefinite integrals because it accounts for the infinite number of possible antiderivative functions that can differentiate back to the original function. It represents the family of functions that are all valid antiderivatives of the integrand.
What should one do if they dislike developing skills through practice and prefer a rote method for choosing u in integration by parts?
-For those who prefer a rote method, the LIATE acronym can be used as a straightforward guide to choose u in integration by parts without needing to deeply understand the functions involved.
How can one verify the result of an integration by parts?
-To verify the result, one can differentiate the result of the integration by parts and check if it equals the original integrand. If the derivative matches the original function, the integration was performed correctly.
Outlines
📚 Introduction to Integration by Parts
The paragraph introduces the concept of integration by parts, a technique used in calculus for integrating products of functions. Nancy explains that while basic integration rules may not apply to more complex integrands, integration by parts provides a solution. She emphasizes the importance of choosing the correct u and dv for the process to be effective, and hints at a trick to aid in this selection. The paragraph sets the stage for a deeper exploration of the integration by parts formula and its application.
🧠 Choosing u and dv: The Key to Success
In this paragraph, Nancy delves into the process of selecting u and dv for integration by parts. She explains that u should be the function that simplifies upon differentiation, while dv should not complicate upon integration. Using the given example of ∫x * e^x dx, she illustrates how to apply these rules and emphasizes the importance of including the differential dx. The paragraph also introduces the concept of du and v, which are derived from u and dv respectively, and are crucial for applying the integration by parts formula.
🎯 The LIATE Acronym: A Helpful Tool
Nancy presents the LIATE acronym as a mnemonic device to assist in choosing u and dv for integration by parts. The acronym stands for Log, Inverse Trig, Algebraic, Trig, and Exponential functions, guiding students through the order in which to consider each function when faced with a product of different types. She applies the trick to the example of ∫x * e^x dx, confirming that x (algebraic) is u and e^x (exponential) is dv. The paragraph also discusses scenarios where the trick may not be definitive, such as when dealing with exponential and trigonometric functions, which are interchangeable in the context of integration by parts.
📝 Applying Integration by Parts: Examples and Considerations
This paragraph provides a comprehensive overview of applying integration by parts through various examples. Nancy explains how to handle different types of integrands, including those with algebraic and trigonometric functions, as well as those with exponential and logarithmic components. She clarifies that the LIATE rule can be adapted in certain cases and emphasizes the need for practice in selecting appropriate u and dv. The paragraph also touches on the application of integration by parts to definite integrals and the potential need to apply the technique multiple times to reach a solution.
Mindmap
Keywords
💡Integration by Parts
💡Product Rule
💡Substitution
💡Derivative
💡Integral
💡u and dv
💡LIATE Acronym
💡Constant of Integration
💡Definite Integral
💡Indefinite Integral
💡Integration by Parts Formula
Highlights
Introduction to integration by parts as a method for integrating products of functions.
The importance of checking if the integrand can be simplified algebraically before applying integration techniques.
The suggestion to try substitution first, even if it might not work, as part of the problem-solving process.
Explanation of the integration by parts formula and its purpose in transforming the integral into a more manageable form.
The rule of thumb for choosing u and dv in integration by parts: the function that simplifies upon differentiation becomes u.
The application of the integration by parts formula to the example integral of x * e^x.
The necessity of remembering to include the differential dx when working with du and v.
The use of the LIATE acronym as a mnemonic device for choosing u in integration by parts.
The clarification that the LIATE acronym is not always foolproof and that sometimes a combination of the acronym and the rule of thumb should be used.
The demonstration of how to apply the integration by parts formula to various types of integrals, including those with algebraic and trigonometric functions.
The mention of the need to perform integration by parts multiple times for certain integrals to reach a solution.
The advice that practice and experience will improve the skill in choosing the correct u and dv for integration by parts.
The reminder to include the constant of integration (+c) when solving indefinite integrals.
The brief mention of the more complex form of the integration by parts formula involving functions f(x) and g(x) and their derivatives.
The encouragement for viewers to apply the integration by parts method even if they do not enjoy calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: