Proof: lim (sin x)/x | Limits | Differential Calculus | Khan Academy
TLDRThe video script presents a comprehensive explanation of the squeeze theorem and its application in proving that the limit of the sine function over x as x approaches 0 is equal to 1. The explanation is supplemented with a visual demonstration using the unit circle and trigonometric definitions, highlighting the relationship between the sine, cosine, and tangent of an angle. The proof involves establishing inequalities and utilizing the properties of the unit circle to show that the limit holds true from both the positive and negative side as x approaches 0.
Takeaways
- 📚 The Squeeze Theorem is used to prove that the limit as x approaches 0 of sine of x over x equals 1.
- 🎨 A visual proof involving the unit circle in trigonometry is provided to support the theorem.
- 📐 The unit circle is defined as a circle with a radius of 1, where sine of x is the y-coordinate of any point on the circle.
- 🔺 The tangent of x is defined as the opposite side over the adjacent side in a right triangle, which relates to the unit circle as tangent of x equals the side length over 1.
- 🔽 The area of the triangle formed by the radius and the line segment from the origin to the point on the unit circle is calculated as 1/2 times the base times the height, where the height is sine of x.
- 🔶 The area of the sector (wedge) formed by the angle x radians is x/2, as it represents x/2 pi of the total 2 pi radians of the unit circle.
- 🔼 The area of the larger triangle, which includes the sector, is 1/2 times the tangent of x, providing a relationship between the areas.
- 📈 An inequality is established stating that the area of the small triangle (1/2 sine of x) is less than the area of the sector (x/2), which is less than the area of the large triangle (1/2 tangent of x).
- 🌐 The inequality holds in the first and fourth quadrants, and by taking absolute values, it is valid for x approaching 0 from both positive and negative directions.
- 🔄 By dividing all parts of the inequality by the absolute value of sine of x, a new inequality is formed, leading to the application of the Squeeze Theorem.
- 🏆 The limit of the function 1 is 1 as x approaches 0, and the limit of cosine of x is also 1 as x approaches 0, setting the boundaries for the Squeeze Theorem application.
- 📊 A graphical representation is provided to illustrate how the function sine of x over x converges to 1 as x approaches 0, confirming the theorem's validity.
Q & A
What is the main theorem being discussed in the transcript?
-The main theorem discussed in the transcript is the Squeeze Theorem, which is used to prove that the limit as x approaches 0 of sine of x over x is equal to 1.
How does the unit circle relate to the problem of finding the limit of sine of x over x as x approaches 0?
-The unit circle is used to visually represent the trigonometric functions and their relationships. It helps in understanding the definitions of sine and tangent in terms of the y-coordinate and the ratio of the opposite side to the adjacent side of a right triangle, respectively.
What is the significance of the first and fourth quadrants in this discussion?
-The first and fourth quadrants are significant because they are the regions where the inequality holds true for the proof. The author emphasizes that the inequality and the limit should be valid in both the first and fourth quadrants as x approaches 0.
How does the author handle the absolute value in the inequality when dealing with the first and fourth quadrants?
-The author introduces absolute values to ensure that the inequality holds true in both the first and fourth quadrants. This is done because the sine and tangent functions can have different signs in these quadrants, but taking the absolute value ensures that the distances and areas remain positive.
What is the role of the green triangle in the proof?
-The green triangle is used to represent the area that is calculated using the sine function. Its area is 1/2 times the sine of x, which is a key component in the inequality that is being developed for the proof.
What is the significance of the wedge shape in the proof?
-The wedge shape represents a larger area that includes the green triangle and the arc of the unit circle. Its area is x/2, which is used to show that the area of the green triangle (sine of x) is less than the area of the wedge as x approaches 0.
How does the author use the tangent function to establish the inequality?
-The author uses the tangent function, which is the ratio of the opposite side to the adjacent side of a right triangle, to establish the upper bound of the inequality. The area of the larger triangle, which is 1/2 times the tangent of x, is used to show that the area of the wedge (x/2) is less than the area of this triangle.
What is the purpose of inverting the inequality in the proof?
-Inverting the inequality allows the author to isolate the expression sine of x over x and to show that it is greater than 1. This is a crucial step in applying the Squeeze Theorem to prove that the limit of this expression as x approaches 0 is 1.
What are the limits of the function 1 and cosine of x as x approaches 0?
-The limit of the function 1 as x approaches 0 is 1, as it is a constant function. The limit of cosine of x as x approaches 0 is also 1, since the cosine function is continuous and its value at 0 is 1.
How does the Squeeze Theorem help in proving the limit of sine of x over x as x approaches 0?
-The Squeeze Theorem allows the author to show that since both 1 (the limit of the function 1 as x approaches 0) and the cosine of x (also 1 as x approaches 0) are on either side of the expression sine of x over x, and this expression is always between them, the limit of sine of x over x must also be 1 as x approaches 0.
What is the visual representation of the proof provided in the transcript?
-The visual representation includes graphs of the functions y=1, y=cos(x), and y=sin(x)/x between -π/2 and π/2. The graph of y=sin(x)/x is shown to be always between the other two functions, which helps to illustrate the Squeeze Theorem in action.
Outlines
📚 Introduction to the Squeeze Theorem and Visual Proof
The paragraph begins with an introduction to the squeeze theorem and its application in proving the limit of the sine function over x as x approaches 0. The explanation is supported by a visual approach, using the unit circle and trigonometric definitions to set up the problem. The unit circle is drawn with an emphasis on the first and fourth quadrants, and the x and y-axes are defined. The concept of sine as the y-coordinate of a point on the unit circle is introduced, and the tangent of x is defined using the SOHCAHTOA mnemonic. The paragraph lays the groundwork for the upcoming mathematical proof by discussing the areas of triangles and wedges formed within the unit circle.
📈 Analyzing Areas and Establishing Inequalities
This paragraph delves into the calculation of areas for different shapes within the unit circle, specifically focusing on a small triangle, a wedge, and a larger triangle. The area of the green triangle is given as 1/2 times the sine of x, the area of the wedge is x/2, and the area of the larger triangle is 1/2 times the tangent of x. Inequalities are established to show that the area of the green triangle is less than that of the wedge, which in turn is less than the area of the larger triangle. The inequalities are analyzed in the context of the first and fourth quadrants, and the absolute value is introduced to maintain the validity of the inequalities when x is negative. The paragraph concludes with a reformulation of the inequalities, simplifying them to emphasize the relationship between the sine, tangent, and x as they approach 0.
🔍 Inverting Inequalities and Applying the Squeeze Theorem
The focus of this paragraph is on inverting the established inequalities and applying the squeeze theorem. By dividing each part of the inequality by the absolute value of sine x and inverting the inequality, a new inequality is formed where 1 is greater than sine x/x, which is greater than the cosine x. The paragraph clarifies that sine x/x is always positive in the first and fourth quadrants, thus eliminating the need for absolute values. The squeeze theorem is then used to prove that the limit of sine x/x as x approaches 0 is equal to 1, based on the fact that the limits of the functions 1 and cosine x as x approaches 0 are both 1.
🎓 Conclusion and Visual Representation of the Proof
The final paragraph concludes the proof that the limit of sine x/x as x approaches 0 is equal to 1. It reiterates the limits of the functions 1 and cosine x as x approaches 0, and reaffirms the application of the squeeze theorem. A visual representation is provided to enhance understanding, showing the graphs of the functions 1, cosine x, and sine x/x between -pi/2 and pi/2. The paragraph emphasizes that the squeeze theorem allows us to deduce the limit of sine x/x by observing that it is always between the limits of the functions 1 and cosine x as x approaches 0.
Mindmap
Keywords
💡Squeeze Theorem
💡Trigonometry
💡Unit Circle
💡Limit
💡Sine Function
💡Cosine Function
💡Tangent Function
💡Inequality
💡Visual Proof
💡Absolute Value
Highlights
The use of the squeeze theorem to prove that the limit as x approaches 0 of sine of x over x equals 1.
The visual proof involving the unit circle and trigonometry.
Defining sine of x as the y-coordinate of any point on the unit circle.
Explaining tangent of x as opposite over adjacent using the SOHCAHTOA definition.
Calculating the area of a triangle using the formula 1/2 times base times height.
Deriving the area of a wedge from the unit circle using radians and the entire circle's area.
Establishing an inequality involving the areas of the triangle and wedge to demonstrate the relationship between sine x, x/2, and tangent x.
Using absolute values to ensure the inequality holds true in both the first and fourth quadrants.
Dividing all parts of the inequality by the absolute value of sine of x to simplify the expression.
Inverting the inequality to get closer to using the squeeze theorem.
Confirming that sine of x over x is always positive in the first and fourth quadrants.
Applying the squeeze theorem with the limits of the function 1 and cosine of x as x approaches 0.
Visualizing the proof with a graph showing the function 1, cosine of x, and sine of x over x between negative pi/2 and pi/2.
The red line (sine of x over x) always being between the dark blue (function 1) and light blue (cosine of x) lines, demonstrating the squeeze theorem in action.
The comprehensive demonstration of the squeeze theorem and its application to trigonometric functions.
The clear explanation of how the areas of geometric figures on the unit circle relate to the values of trigonometric functions.
The logical progression from establishing the inequality to applying the squeeze theorem for the limit proof.
Transcripts
Browse More Related Video
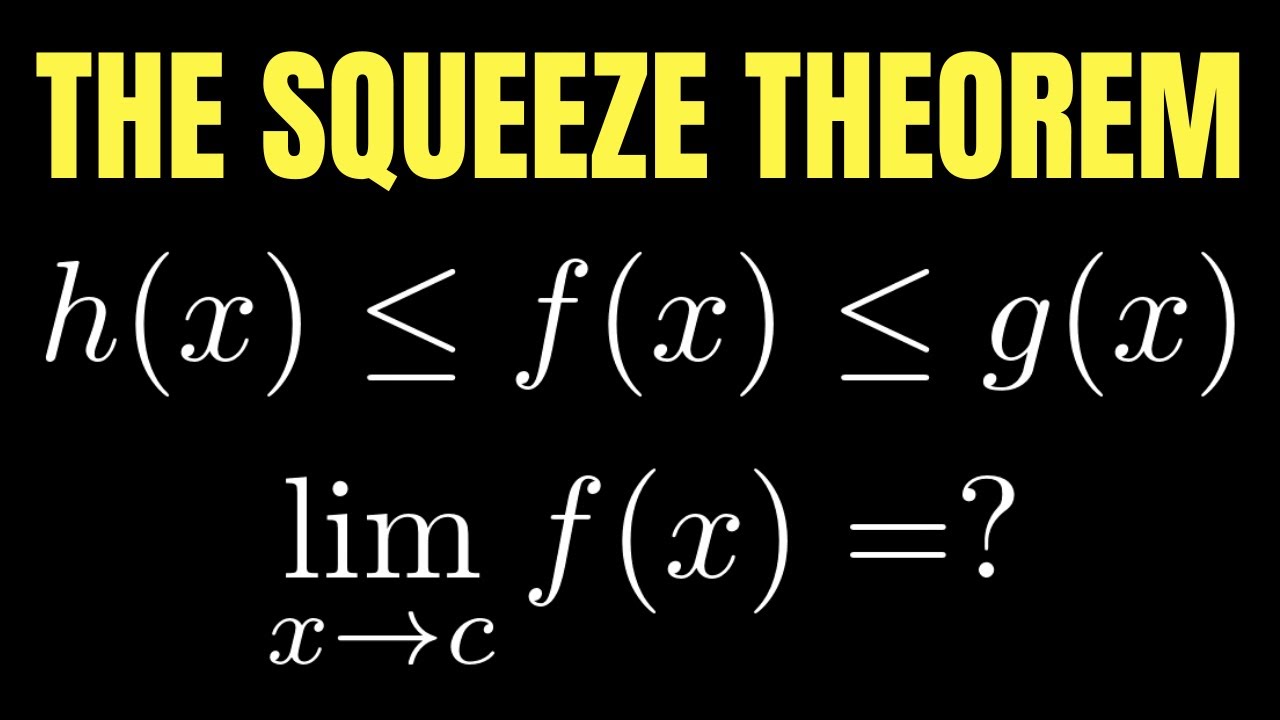
Calculus: The Squeeze Theorem Full Tutorial

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus
The Limit (do not use L'Hospital rule)
Limits of Oscillating Functions and the Squeeze Theorem

Squeeze Theorem for Limits (1)

Limit of sin(x)/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: