Limits of Oscillating Functions and the Squeeze Theorem
TLDRThe video script delves into the mathematical concept of limits, specifically focusing on the behavior of the function 'sine of 1 over X' as X approaches zero from the right. Initially, the script explains that the sine function oscillates between -1 and 1, and when applied to '1 over X', it leads to rapid oscillations as X nears zero. This results in the function not approaching a single value, thus the limit does not exist. The script then introduces a modified function, 'X times sine of 1 over X', which is bounded by X and -X, creating an 'envelope' that confines the oscillations. As X approaches zero, this function is 'squeezed' towards zero, leading to the conclusion that its limit is indeed zero. This is demonstrated using the Squeeze Theorem, which states that if two functions bound a third and both approach the same limit, the middle function must also approach that limit. The theorem is applied to show that 'X sine of 1 over X' is bounded between X and -X, both of which tend to zero as X approaches zero from the right, hence proving the limit of the function to be zero.
Takeaways
- 📉 The limit of \( \sin(1/x) \) as \( x \) approaches 0 from the right does not exist because the function oscillates infinitely between -1 and 1.
- 📈 When \( x \) is multiplied with \( \sin(1/x) \), the function is bounded by \( x \) and \( -x \), creating an 'envelope' that limits the oscillation.
- 🔢 The function \( x \cdot \sin(1/x) \) approaches 0 as \( x \) approaches 0 from the right, due to the multiplication by \( x \) which diminishes the oscillation effect.
- 🧮 The Squeeze Theorem is utilized to determine the limit of functions that are bounded between two other functions, both of which have the same limit.
- 🟢 In the given example, \( x \) and \( -x \) serve as the bounding functions with the same limit of 0 as \( x \) approaches 0 from the right.
- 🔑 The Squeeze Theorem states that if the limits of the bounding functions are equal, the limit of the function in between must also be equal to that value.
- 📌 The sine function, \( \sin(x) \), oscillates between -1 and 1, which is a fundamental property used in bounding \( \sin(1/x) \).
- 📊 The graph of \( \sin(1/x) \) shows rapid oscillation as \( x \) gets closer to 0, which is visualized as a compressed oscillation between -1 and 1 on the graph.
- 🤔 The concept of limits is central to understanding the behavior of functions near certain points, especially points of discontinuity like 0 in this case.
- 📚 Mathematical notation and graphical representation are essential tools for visualizing and solving limit problems in calculus.
- 📘 Understanding the behavior of trigonometric functions, such as \( \sin(x) \), is crucial for analyzing more complex functions like \( \sin(1/x) \).
Q & A
What does the term 'limit' in calculus refer to?
-In calculus, the term 'limit' refers to the value that a function or sequence 'approaches' as the input (or index) approaches some point. It is a fundamental concept in understanding continuity, derivatives, and integrals.
What is the behavior of the sine function as X approaches zero?
-The sine function oscillates between -1 and 1, and as X approaches zero, it does not approach a single value but instead oscillates infinitely fast between -1 and 1.
What is the graphical representation of sine of 1 over X as X approaches zero?
-The graph of sine of 1 over X shows rapid oscillations between -1 and 1 as X approaches zero, with the oscillations becoming more frequent as X gets closer to zero.
How does multiplying the function sine of 1 over X by X affect its limit as X approaches zero?
-Multiplying the function sine of 1 over X by X creates a new function that is bounded between X and -X. As X approaches zero from the right, the oscillations are 'dragged down' to zero by the multiplying factor X, resulting in the limit being zero.
What is the Squeeze Theorem and how is it applied in this context?
-The Squeeze Theorem, also known as the Sandwich Theorem, states that if two functions have the same limit as they approach a certain point and a third function is bounded between them, then the third function also has the same limit. In this context, it is used to show that the limit of X times sine of 1 over X as X approaches zero is zero.
What are envelope functions and how do they relate to the function X sine of 1 over X?
-Envelope functions are bounding functions that 'contain' another function between them. In the context of X sine of 1 over X, the envelope functions are X and -X, which bound the oscillations of the function between them as X approaches zero.
Why does the limit of sine of 1 over X not exist as X approaches zero from the right?
-The limit does not exist because the function sine of 1 over X oscillates between -1 and 1 infinitely fast as X approaches zero, never settling on a single value.
What is the significance of the function oscillating between -1 and 1 for the sine function?
-The oscillation between -1 and 1 is a fundamental property of the sine function, which is periodic and reflects the behavior of a wave. This property is important for understanding the limits of more complex functions like sine of 1 over X.
How does the concept of limits relate to the idea of continuity in functions?
-The concept of limits is crucial for defining continuity. A function is continuous at a point if the limit of the function as it approaches that point is equal to the function's value at that point. Understanding limits helps in determining where a function is continuous or discontinuous.
What is the domain of the function X sine of 1 over X?
-The domain of the function X sine of 1 over X is all real numbers except for X = 0, since the function is undefined at that point (division by zero is undefined).
Can you provide an example of a function that does not oscillate as X approaches zero?
-A simple example of a function that does not oscillate as X approaches zero is a linear function, such as f(X) = 2X. As X approaches zero, the value of the function simply approaches zero without oscillation.
What is the limit as X approaches zero from the right of the function X sine of 1 over X, according to the Squeeze Theorem?
-According to the Squeeze Theorem, the limit as X approaches zero from the right of the function X sine of 1 over X is 0, as it is bounded between the functions X and -X, both of which approach 0 at that limit.
Outlines
📉 Oscillation of Sine(1/X) as X Approaches Zero
This paragraph discusses the behavior of the function Sine(1/X) as X approaches zero from the right. The sine function is known for its oscillatory nature, oscillating between -1 and 1. When considering Sine(1/X), as X gets closer to zero, the values inside the sine function become extremely large, leading to rapid oscillations. The graph of Sine(1/X) is expected to oscillate very quickly around zero, without approaching a single value. This is due to the fact that for very small intervals around zero, the function is inputting very large numbers, resulting in a compressed oscillation between -1 and 1. The limit of Sine(1/X) as X approaches zero from the right does not exist, as it does not settle on a single value but rather oscillates infinitely fast.
🔢 Squeeze Theorem Application to X * Sine(1/X)
The second paragraph explores the application of the squeeze theorem to the function X * Sine(1/X) as X approaches zero from the right. Unlike the previous case, this function includes an additional factor of X, which ensures that as X approaches zero, the entire function also approaches zero. The graph of X * Sine(1/X) is bounded by the envelope functions X and -X, as the product of X and Sine(1/X) will always lie between these two bounds. By applying the squeeze theorem, which states that if two functions S and H bound a function G from below and above respectively and both S and H have the same limit L as X approaches a certain value, then G must also have the limit L, it is concluded that the limit of X * Sine(1/X) as X approaches zero from the right is zero. This is because both bounding functions, X and -X, have the limit of zero at this point, thus forcing the function of interest, X * Sine(1/X), to also have a limit of zero.
Mindmap
Keywords
💡Limit
💡Sine Function
💡Oscillation
💡Envelope Function
💡Squeeze Theorem
💡Trigonometric Function
💡Graph
💡Approaching Zero
💡Function
💡Domain
💡Bounds
Highlights
Investigating the limit of sine(1/X) as X approaches zero from the right.
Sine of X oscillates between -1 and 1, and as X approaches zero, the value inside the sine function becomes very large.
The graph of sine(1/X) will oscillate very quickly in a small interval around zero.
The limit of sine(1/X) as X approaches zero from the right does not exist due to infinite oscillation.
Introducing an extra factor of X in the function, changing the behavior as X approaches zero.
The function X times sine(1/X) is bounded by X and -X, creating an 'envelope' for the oscillation.
The limit of X times sine(1/X) as X approaches zero from the right is concluded to be zero.
Application of the Squeeze Theorem to determine limits where the function of interest is bounded by two other functions.
If the limits of the bounding functions are equal, the limit of the function in between must also be the same.
The Squeeze Theorem is used to deduce that the limit of X sine(1/X) as X approaches zero from the right is zero.
Fundamental bounds on the sine function are used to establish the limits for the Squeeze Theorem application.
Minus X is always smaller than X sine(1/X), which is always less than X for X > 0.
The limit as X goes to zero from the right of both X and -X is zero, enabling the use of the Squeeze Theorem.
The function X sine(1/X) is 'squeezed' between X and -X, leading to the conclusion that its limit is also zero.
The Squeeze Theorem is a powerful tool for finding limits where direct calculation is difficult.
The theorem provides a way to extrapolate from known limits to deduce the limit of a related function.
Understanding the behavior of functions as they approach certain values is crucial in calculus and analysis.
The concept of limits is fundamental to the study of calculus, particularly in understanding the behavior of functions at specific points.
Transcripts
Browse More Related Video

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus

Squeeze Theorem for Limits (1)
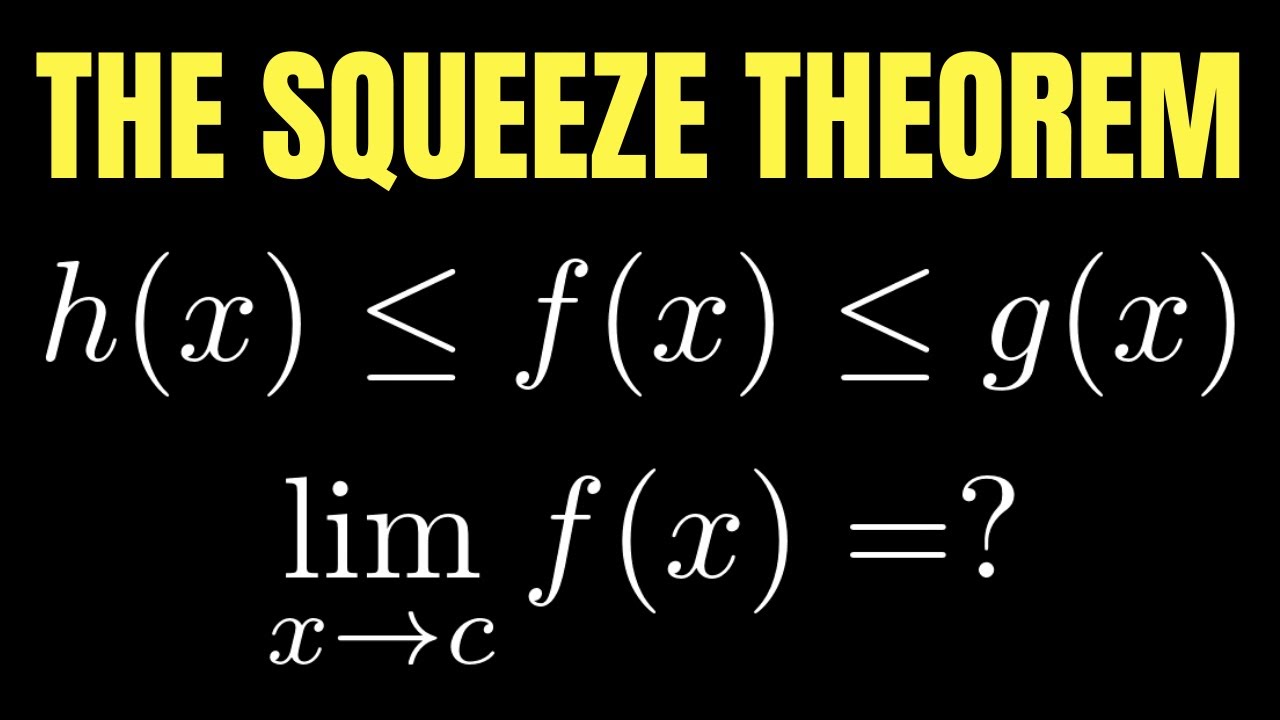
Calculus: The Squeeze Theorem Full Tutorial

Zero-Bounded Limit Theorem (with example)

Limit at a point of discontinuity

Differentiability at a point: algebraic (function isn't differentiable) | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: