AP Calculus AB: Evaluating Transcendental Limits

JJ Sandoval
27 Aug 202009:26
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the instructor skillfully navigates through the complexities of transcendental functions, demonstrating how to resolve indeterminate forms by rewriting expressions and simplifying limits. They cover essential trigonometric identities and algebraic manipulations to find limits of functions as they approach specific values, such as pi/2 and pi/4, using the unit circle and algebraic simplification techniques. The video also tackles exponential functions, showcasing how to simplify complex fractions and factor expressions to find the limit as x approaches zero, ultimately emphasizing the importance of algebraic skills in calculus.

Takeaways
  • 📚 The essence of transcendental functions is to evaluate limits that initially appear indeterminate, such as cos(π/2) or cot(π/2), which both yield zero and result in an indeterminate form of 0/0.
  • 🔄 To resolve indeterminate forms, one can use algebraic manipulation, such as rewriting cotangent as cosine over sine and then multiplying by the reciprocal to simplify the expression.
  • 📉 When approaching the limit as x approaches π/2, the sine function can be used to simplify the expression, resulting in a limit of sine of π/2, which is 1.
  • 🔍 For the limit involving tangent of π/4, the expression can be rewritten using the identity tan(x) = sin(x)/cos(x) to simplify the complex fraction and find the limit as x approaches π/4.
  • 🔢 In cases of zero over zero, rewriting the expression to eliminate the zero in the denominator can help find the limit, such as factoring out terms or using properties of exponents.
  • 🌐 The unit circle is a useful tool for evaluating trigonometric functions at specific angles, like sine of π/2, which corresponds to the point (0, 1) on the unit circle.
  • 📝 Algebraic skills are crucial for rewriting expressions to find limits, especially when dealing with complex fractions or exponential functions.
  • 🔗 The identity e^x - 1 can be factored to simplify expressions involving exponential functions, which is useful for finding limits as x approaches 0.
  • 📉 The limit of sine of x over x as x approaches 0 is a common form that can be used to simplify other limits involving trigonometric functions.
  • 🔑 Constants can be taken outside the limit function, allowing for easier manipulation of the expression inside the limit.
  • 🔄 Multiplying the numerator and denominator by a constant can help match the form of a known limit, such as multiplying by 3 to match the form of sine of 3x over 3x.
Q & A

  • What is the indeterminate form that arises when plugging in the value of pi/2 into the expression cotangent(pi/2)?

    -The expression cotangent(pi/2) results in an indeterminate form of 0/0 because cosine(pi/2) is 0, and cotangent is defined as cosine over sine.

  • How can the cotangent function be rewritten to avoid the indeterminate form when x approaches pi/2?

    -Cotangent can be rewritten as the reciprocal of tangent, which is sine over cosine. This allows us to avoid the indeterminate form by multiplying by the reciprocal of the denominator.

  • What is the value of sine(pi/2) on the unit circle?

    -The value of sine(pi/2) on the unit circle is 1, as pi/2 corresponds to the point (0,1) where the y-coordinate represents the sine value.

  • What is the tangent of pi/4 and how does this affect the expression involving sine and cosine when x approaches pi/4?

    -The tangent of pi/4 is 1. This affects the expression because when x approaches pi/4, the sine and cosine values are both square root of 2 over 2, leading to an indeterminate form of 0/0.

  • How can the expression involving tangent and sine minus cosine be simplified when x approaches pi/4?

    -The expression can be simplified by rewriting tangent as sine over cosine and then multiplying by the reciprocal of the denominator to eliminate the indeterminate form, resulting in a new expression that can be simplified further.

  • What is the result of the limit as x approaches 0 for the expression e^x - 1 / x - 1?

    -The result of the limit as x approaches 0 for the given expression is 1, as the numerator simplifies to 0 and the denominator also approaches 0, but after rewriting the expression, it simplifies to 1/e^0 which is 1.

  • How does the script suggest rewriting the expression involving e^x when faced with an indeterminate form of 0/0?

    -The script suggests rewriting the expression by factoring out e^x - 1 and then multiplying by the reciprocal of the denominator, e^x, to simplify the complex fraction and resolve the indeterminate form.

  • What is the final simplified result of the limit as x approaches 0 for the expression (e^x - 1) / (x - 1)?

    -The final simplified result of the limit is 1, as after rewriting and simplifying, the expression becomes 1/e^0 when x is 0.

  • What is the strategy used in the script to evaluate the limit of (x^2 - 1) / (e^x - 1) as x approaches 0?

    -The strategy is to factor the numerator as a difference of squares, (x - 1)(x + 1), and then simplify the expression by canceling out terms, leading to a limit that evaluates to 4 as x approaches 0.

  • How is the limit of sine(3x) / x evaluated as x approaches 0 in the script?

    -The limit is evaluated by factoring out a constant and then using the property of limits that allows us to take constants out of the limit expression, resulting in a new limit of sine(3x) / 3x, which simplifies to 3/2 when x is 0.

Outlines
00:00
📚 Understanding Indeterminate Forms in Trigonometry

This paragraph explains how to handle indeterminate forms in trigonometric functions, specifically focusing on the limit as x approaches π/2 for cotangent and tangent functions. The speaker demonstrates how to rewrite these functions to avoid indeterminate forms, using the reciprocal relationship between sine and cosine. The example of cotangent at π/2 is used to illustrate the process, resulting in a simplified expression that leads to a limit of sine at π/2, which is 1. The paragraph also covers the handling of tangent at π/4, showing how to rewrite it to avoid division by zero and ultimately find the limit.

05:01
🔍 Algebraic Manipulation to Solve Limits

The second paragraph delves into solving complex limits using algebraic manipulation. The speaker begins by addressing a limit that results in 0/0 after plugging in the value 0, and then shows how to rewrite the expression with negative exponents as a fraction. The example provided involves multiplying by e^x to both the numerator and denominator to simplify the expression, leading to a limit of 1 as x approaches 0. The paragraph also covers another example where the expression can be factored, simplifying the limit to 4 times (e^x + 1) as x approaches 0, which results in 8 when x is substituted with 0. The speaker emphasizes the importance of algebraic skills in solving these types of problems.

Mindmap
Keywords
💡Transcendental functions
Transcendental functions are mathematical functions that are not algebraic, meaning they cannot be expressed using a finite number of algebraic operations such as addition, multiplication, and root extraction. In the video, the concept is introduced to explain why certain functions result in indeterminate forms, such as '0/0', when specific values are plugged in.
💡Indeterminate form
An indeterminate form in calculus occurs when the limit of a function results in an expression like '0/0' or '∞/∞', which does not provide a clear value. The script discusses how to rewrite expressions to avoid these forms and find the actual limit of the function as x approaches a certain value.
💡Cotangent
Cotangent is a trigonometric function defined as the reciprocal of the tangent function, which is sine over cosine. In the script, the instructor demonstrates how to rewrite cotangent as cosine over sine to simplify the expression and find the limit as x approaches π/2.
💡Reciprocal
The reciprocal of a number is 1 divided by that number. In the context of the video, the reciprocal is used to rewrite the cotangent function and to simplify complex fractions, which is a key step in finding limits of transcendental functions.
💡Unit circle
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate system. It is used in trigonometry to define and visualize sine and cosine values. In the script, the unit circle is referenced to determine the sine of π/2, which is 1.
💡Tangent
Tangent is a trigonometric function that measures the ratio of the length of the opposite side to the length of the adjacent side in a right-angled triangle. In the video, the instructor explains how to rewrite tangent in terms of sine and cosine to simplify expressions and find limits.
💡Complex fraction
A complex fraction is a fraction where the numerator or the denominator contains a fraction itself. In the script, the instructor demonstrates how to simplify complex fractions by multiplying by the reciprocal of the denominator to find the limit of a function.
💡Factoring
Factoring is the process of breaking down a polynomial or expression into a product of simpler expressions. In the video, the instructor uses factoring to simplify expressions involving exponential functions and to avoid indeterminate forms.
💡Exponential function
An exponential function is a mathematical function of the form f(x) = a * b^x, where 'a' and 'b' are constants, and 'b' is not equal to 1. In the script, the instructor discusses limits involving exponential functions and how to simplify them using algebraic techniques.
💡Limit
In calculus, a limit is the value that a function or sequence approaches as the input or index approaches some value. The script focuses on finding the limits of various functions as x approaches specific values, illustrating the process of simplifying expressions to determine these limits.
💡Algebraic skills
Algebraic skills refer to the ability to manipulate and solve equations using algebraic methods. Throughout the video, the instructor emphasizes the importance of these skills in rewriting and simplifying expressions to find limits of functions.
Highlights

Introduction to transcendental functions and indeterminate forms.

Rewriting cotangent as cosine over sine to simplify expressions.

Using the reciprocal to transform division into multiplication.

Simplifying limits by rewriting expressions involving sine and cosine.

Determining the limit of sine at pi/2 to be one using the unit circle.

Rewriting tangent in terms of sine and cosine to avoid indeterminate forms.

Simplifying complex fractions by multiplying by the reciprocal of the denominator.

Factoring out terms to simplify limits involving exponential functions.

Using algebraic manipulation to find the limit of e^x - 1 as x approaches 0.

Handling negative zero by recognizing it as simply zero.

Rewriting negative exponents as fractions to simplify limits.

Applying algebraic skills to rewrite and simplify complex limit expressions.

Using the factorization method to simplify limits involving e^x.

Demonstrating the limit of a function as x approaches 0 by simplifying the expression.

Multiplying by constants outside the limit to simplify sine functions.

Final simplification of limits to a constant value using algebraic techniques.

Emphasizing the importance of algebraic skills in solving transcendental limits.

Transcripts

Browse More Related Video

Limit examples w/ brain malfunction on first prob (part 4) | Differential Calculus | Khan Academy

Calculus AB/BC – 1.6 Determining Limits Using Algebraic Manipulation

Rational Expressions Review

How to Find Any Limit: Part 2 (NancyPi)

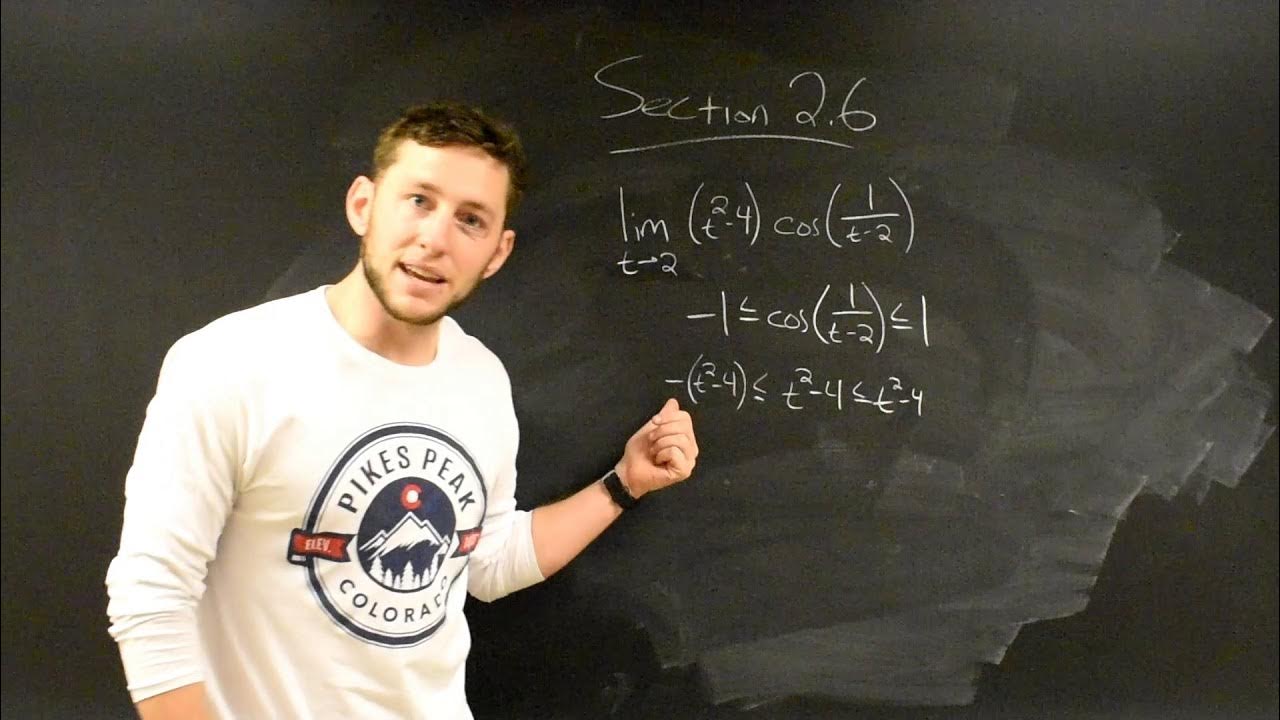
Limits Involving Sine and Cosine & The Squeeze Theorem!

How to Find the Limit at Infinity (NancyPi)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Math TutorialTranscendental FunctionsAlgebra SkillsLimit CalculationEducational ContentTrigonometry LimitsCotangentTangentSine and CosineE to the XFactoring Techniques