Homogeneous Differential Equations
TLDRThis video script provides a comprehensive guide on solving homogeneous differential equations. It begins with an example where the equation involves terms of the same degree, explaining the characteristic of homogeneity. The solution process involves substituting y with vx, differentiating using the product rule, and simplifying to separate variables. The script then demonstrates integrating both sides and solving for y in terms of x, illustrating the steps with clear calculations. The video continues with additional examples, each time applying the substitution and integration method to reach the general solution. The final step in each example includes using an initial condition to find the constant of integration. The script concludes with a summary of the method for solving homogeneous differential equations, emphasizing the importance of recognizing the degree of terms and the systematic approach to finding the solution.
Takeaways
- 📚 A homogeneous differential equation is one where all terms are of the same degree, typically the first degree.
- ➗ To solve such an equation, replace y with v*x and use the product rule to differentiate, resulting in dy = x*dv + v*dx.
- 🔄 After substitution, simplify and separate the variables so that all x terms are on one side and all v or y terms are on the other.
- 🧮 Integrate both sides of the equation after separating variables, which typically involves finding antiderivatives.
- 🔗 Use properties of logarithms to simplify expressions, such as moving coefficients in and out of logarithms and combining logarithms using multiplication.
- 🟰 Set the inside of the natural logarithm on both sides of the equation equal to each other to find the relationship between v and x.
- 🆗 Replace v with y/x to get the solution in terms of the original variables.
- 🟢 When given an initial condition, substitute the values into the general solution to find the constant of integration.
- 🟡 The final solution is often expressed in terms of exponential and logarithmic functions, which are the integral results of the separated variables.
- ✅ Always check the solution against the original differential equation to ensure it satisfies the conditions.
- 🔢 For complex solutions, use algebraic manipulation and properties of exponents and logarithms to simplify the expression into a more understandable form.
- 📉 In the context of differential equations, exponential terms are often considered homogeneous even if they are not explicitly polynomials.
Q & A
What is a homogeneous differential equation?
-A homogeneous differential equation is a differential equation where each term is of the same degree. In the context of the video, it specifically refers to equations where all terms are of the first degree.
How do you solve a homogeneous differential equation?
-To solve a homogeneous differential equation, you can use a substitution method where you replace 'y' with 'v times x' and then differentiate using the product rule. After that, you can simplify, separate variables, and integrate both sides to find the solution.
What is the first step in solving the given example of a homogeneous differential equation?
-The first step is to replace 'y' with 'v times x' and 'dy' with 'x dv + v dx', and then simplify the equation to prepare it for separation of variables.
How do you separate the variables in the equation?
-You separate the variables by dividing both sides of the equation by the terms that include 'x' and 'v', effectively isolating 'dv' on one side and 'dx' on the other, which allows you to integrate each side separately.
What is the importance of integrating both sides of the equation after separating variables?
-Integrating both sides of the equation after separating variables allows you to find the antiderivative, which leads to the general solution of the differential equation in terms of 'y' and 'x'.
How do you handle the constant of integration?
-The constant of integration, typically denoted as 'c', is added to the right side of the equation after integrating. It represents an arbitrary constant that can take on any value and accounts for the fact that the derivative does not determine the function uniquely.
What is the final form of the solution to the first homogeneous differential equation example in the video?
-The final form of the solution is the absolute value of x equals c times (x - y squared), where 'c' is a constant.
How do you solve a homogeneous differential equation with an initial condition?
-You solve a homogeneous differential equation with an initial condition by first finding the general solution of the equation, and then using the initial condition to find the specific value of the constant in the solution.
What is the significance of the exponential term in a homogeneous differential equation, and how does it affect the solution process?
-The exponential term does not affect the degree of the equation and is therefore not counted when determining homogeneity. It can be treated as part of the first-degree term during the solution process, which involves integration after separating variables.
How do you use the initial condition (1,0) to find the value of the constant 'c' in the solution?
-You substitute the initial condition values into the general solution to form an equation for 'c'. For the condition (1,0), you would substitute x=1 and y=0 into the solution and solve for 'c'.
What is the final solution to the differential equation with the initial condition (1,0) as given in the video?
-The final solution, after applying the initial condition (1,0), is e raised to the power of y over x equals 1 plus the natural logarithm of x squared.
Outlines
📚 Introduction to Homogeneous Differential Equations
This paragraph introduces the concept of homogeneous differential equations, emphasizing that each term within such an equation must be of the same degree, typically the first degree. The example provided is a differential equation involving 'x' and 'y', and the method to solve it is outlined. The process includes substituting 'y' with 'v times x', differentiating using the product rule, and simplifying the equation to separate and integrate the variables.
🔍 Solving the First Homogeneous Differential Equation
The paragraph walks through the steps to solve a specific homogeneous differential equation. It involves replacing 'y' with 'v times x', differentiating, and simplifying to separate variables. The solution process includes factoring, dividing by 'x', and integrating both sides of the equation. The final solution is expressed in terms of 'y' and 'x', and a method to simplify the complex fraction is explained.
📝 Approaching a Second Homogeneous Differential Equation
This section begins by confirming the homogeneity of a second differential equation due to all terms being of the second degree. The method to solve it involves replacing 'y prime' with 'dy/dx', cross-multiplying, and substituting 'y' with 'v times x'. The process requires differentiating, factoring out 'x squared', and simplifying the equation. The separation of variables and integration follows, leading to the solution in terms of 'v' and 'x'.
🧮 Completing the Integration for the Second Equation
The paragraph focuses on completing the integration process for the second equation. It involves rewriting the integral, applying the power rule, and integrating both sides. The solution is simplified by replacing 'v' with 'y/x', and using logarithmic properties to combine terms. The final step is to express the solution in terms of 'y' and 'x', and to square both sides to solve for 'y'.
🔗 Applying an Initial Condition to Find a Specific Solution
In this part, an initial condition (x=1, y=0) is given to find the value of the constant 'c' in the general solution of a homogeneous differential equation. The process involves substituting the initial condition into the general solution, solving for 'c', and then using this value to write the final answer. The solution is simplified by using properties of exponents and logarithms.
📉 Finalizing the Solution with the Initial Condition
The final paragraph ties up the solution by applying the initial condition to the general equation derived from the differential equation. It demonstrates the calculation of the constant 'c' and the simplification of the equation to its final form. The solution is expressed in a simplified exponential form involving 'y', 'x', and the natural logarithm of 'x'.
Mindmap
Keywords
💡Homogeneous Differential Equation
💡Separation of Variables
💡Product Rule
💡Integration
💡Natural Logarithm
💡Anti-Derivative
💡Initial Value
💡Exponential Function
💡Complex Fraction
💡Absolute Value
💡Constant of Integration
Highlights
The video discusses how to solve homogeneous differential equations, which have all terms in the same degree.
A substitution method is introduced where y is replaced with v times x, and the function is differentiated using the product rule.
The derivative of y (dy) is expressed in terms of x, dv, and vdx after substitution.
The equation is simplified by factoring out x and canceling common terms.
The variables are separated by dividing both sides by 2x and 1 - v, leading to an integrable form.
Integration yields the natural logarithm function, which is then manipulated to solve for v in terms of x.
The solution involves expressing y in terms of v and x, and simplifying the resulting complex fraction.
The final answer for the first problem is presented as an equation involving the absolute value of x and y.
A second example is solved, illustrating the process with a different homogeneous differential equation.
The video demonstrates the cross-multiplication and substitution method to transform the equation into a separable form.
Integration of both sides of the transformed equation leads to the natural logarithm of v and x.
The constants are isolated, and the solution is expressed in terms of y and x using logarithmic properties.
The video concludes with a third example that includes an initial condition to find the specific value of the constant c.
The method of separation of variables is applied to the third example, resulting in an integral to solve.
The antiderivative of the equation terms is found, and the constant c is determined using the initial condition.
The final solution of the third problem is an equation relating e to the power of y over x and the natural logarithm of x squared plus one.
The video provides a comprehensive guide on solving homogeneous differential equations using substitution, separation of variables, and integration techniques.
Transcripts
Browse More Related Video

Initial Value Problem

Separable differential equations introduction | First order differential equations | Khan Academy

First order, Ordinary Differential Equations.
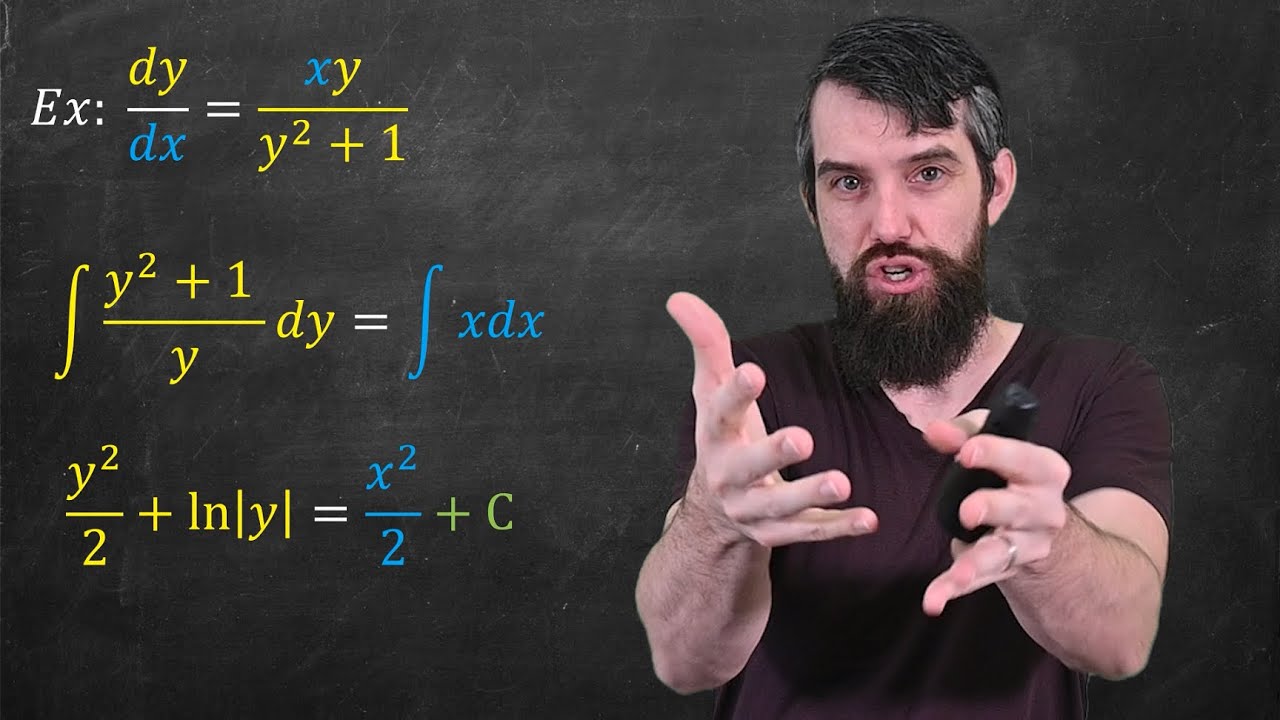
Separation of Variables // Differential Equations
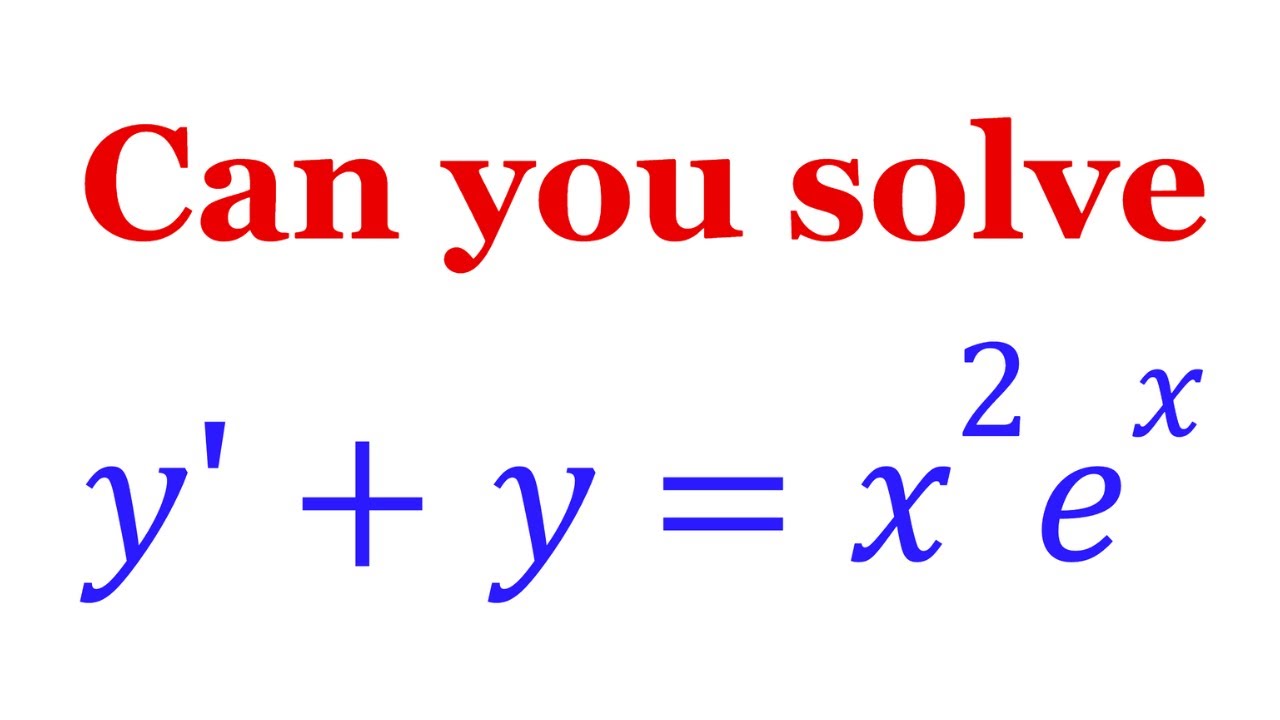
Let's Solve An Interesting Differential Equation

2011 Calculus AB free response #5c. | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: