a very interesting differential equation

Michael Penn

31 Jan 202421:26

EducationalLearning

32 Likes 10 Comments

TLDRIn this lecture, the instructor explores a nonlinear differential equation, \( y y' = (y')^2 \). They emphasize its nonlinearity due to the quadratic term in the dependent variable and its derivatives. By substituting \( z = y' \), they transform it into a second-order differential equation. Various cases are solved using separation of variables, integrating factors, and substitutions, ultimately deriving solutions for different scenarios. The lecture provides a comprehensive analysis of solving complex nonlinear differential equations, highlighting key techniques and methods.

Takeaways

📚 The script discusses a nonlinear second-order differential equation \( y'' = y' \cdot y' \) and its properties.
🔍 It identifies the equation as autonomous and nonlinear due to the quadratic term \( y' \cdot y' \).
🔑 A substitution method is introduced by setting \( Z = y' \) to simplify the equation to a new form involving \( Z \) and its derivatives.
🧩 The script uses the chain rule to transform the equation into a form that resembles the derivative of a function squared, \( \frac{d}{dx}(Z^2) \).
📉 By recognizing the derivative of \( Z^2 \), the equation is further simplified to \( 2Z' = Z^2 + C \), where \( C \) is a constant.
📈 The solution process involves considering different cases for the constant \( C \), including \( C = 0 \), \( C > 0 \), and \( C < 0 \).
📝 For \( C = 0 \), the method of separation of variables is used to find the solution involving natural logarithms.
📚 When \( C > 0 \), the solution involves the arctangent function and the natural logarithm of secant.
📉 For \( C < 0 \), partial fraction decomposition is used, leading to an exponential form of the solution.
🔄 The final solutions for different cases are expressed in terms of exponential and logarithmic functions, showcasing the diversity of solutions for differential equations.
🔍 The script concludes with a comprehensive solution that includes integrals and substitutions to solve for \( y \) in terms of \( x \).

Q & A

What type of differential equation is discussed in the transcript?
-The differential equation discussed is a nonlinear differential equation, specifically an autonomous differential equation where the dependent variable and its derivatives make the equation nonlinear.
Why is the given differential equation considered nonlinear?
-The equation is considered nonlinear because it includes a term that involves the product of derivatives (y' * y'), making it quadratic in the dependent variable Y and its derivatives.
What substitution is introduced to simplify the original differential equation?
-The substitution introduced is setting Z equal to Y', which simplifies the original equation by reducing it to a second-order nonlinear differential equation.
How is the chain rule applied in the context of this differential equation?
-The chain rule is applied by recognizing that the right-hand side of the equation, Z * Z', can be expressed as the derivative of Z^2 with respect to X, simplifying the equation further.
What is the solution approach when the constant 'a' equals zero?
-When 'a' equals zero, the solution approach involves separating variables, integrating both sides, and solving for Y, leading to a solution involving the natural logarithm of the variable X.
How is the arc tangent function used in the solution for the case when 'a' is positive?
-For the case when 'a' is positive, the arc tangent function is used after separating variables and integrating, leading to a solution for Z in terms of the tangent of a linear function of X.
What is the significance of renaming constants during the solution process?
-Renaming constants, such as replacing B with e^B, helps simplify the expression and makes it easier to manipulate and solve the differential equation.
How does the method of separation of variables help in solving the equation?
-Separation of variables allows for the differential equation to be split into simpler parts that can be integrated individually, leading to a more straightforward solution for Y.
What final form does the solution take in the case when 'a' is positive with a minus sign?
-The final solution in this case involves the natural logarithm of a quotient involving exponential functions, specifically expressing Y in terms of a natural logarithm that includes a difference of squares in the denominator.
What is the overall strategy for solving the original third-order nonlinear differential equation?
-The overall strategy involves making a substitution to reduce the order of the equation, applying the chain rule, using separation of variables, and carefully managing constants to integrate and solve for Y, depending on the value of the constant 'a'.

Outlines

00:00

🔍 Exploring a Nonlinear Differential Equation

This paragraph introduces the differential equation \( y \cdot y' = (y')^2 \), highlighting its nonlinearity due to the quadratic nature of the term involving \( y' \). The discussion covers the equation's classification as autonomous and nonlinear, and an initial approach to solving it by substitution. The author then introduces a new variable \( z = y' \), transforming the equation into a second-order nonlinear equation. A key insight involves recognizing a pattern resembling the chain rule, allowing further simplification.

05:02

📐 Separation of Variables and Antiderivatives

The author proceeds with the solution by applying the method of separation of variables. The transformed equation \( 2 \cdot \frac{dz}{dx} = z^2 \) is separated into terms involving \( z \) and \( x \). After integrating both sides, the equation is simplified, yielding an expression for \( z \), which corresponds to \( y' \). The paragraph concludes by finding the antiderivative of this expression to derive a function for \( y \), completing the solution for the case when the constant \( a \) is zero.

10:04

📏 Handling the Case with Positive \( a \)

In this paragraph, the author tackles the more complex scenario where the constant \( a \) is positive. Using separation of variables again, the differential equation is transformed and integrated. The antiderivative for the left-hand side involves the arctangent function, and after some algebraic manipulation, the equation for \( z \) (which equals \( y' \)) is obtained. Finally, the author derives the solution for \( y \) by integrating the obtained expression for \( y' \), resulting in a solution involving the natural logarithm of the secant function.

15:08

⚖️ Decomposing the Fraction for the Minus Case

This paragraph focuses on the scenario where \( a \) is positive, but the differential equation involves a minus sign. The author begins by separating the variables and then addresses the integral on the left side through partial fraction decomposition. After deriving the antiderivative, the equation is further simplified by exponentiating both sides. The solution is expressed in terms of \( Z \) and eventually transformed back to \( y' \). The paragraph concludes by presenting the integrated solution for \( y \), which includes a logarithmic expression.

20:09

🧩 Final Simplification and Conclusion

In this concluding paragraph, the author combines the solutions from the previous cases. By further simplifying the expression for \( y \), involving natural logarithms and exponentials, the final form of the solution is derived. The author manipulates the equation to achieve a more elegant expression, suitable for the original differential equation. This final step completes the discussion and provides a neat, closed-form solution to the complex nonlinear differential equation introduced at the beginning.

Mindmap

Keywords

💡Differential Equation

A differential equation is an equation that relates a function with its derivatives. In the script, the main focus is on solving a specific nonlinear differential equation, which is a fundamental concept in calculus and mathematical physics. The differential equation in question is \( y'' = y' \cdot y' \), where \( y' \) and \( y'' \) represent the first and second derivatives of \( y \) with respect to \( x \), respectively.

💡Nonlinear

Nonlinear refers to a property of a differential equation where the dependent variable and its derivatives appear as a non-linear combination. In the video, the term is used to describe the differential equation \( y'' = y' \cdot y' \), which is nonlinear because it involves the product of the first derivative, making it a quadratic function of \( y \) and its derivatives.

💡Autonomous

An autonomous differential equation is one that does not explicitly contain the independent variable, often referred to as 'time' in physical contexts. In the script, the equation is noted as autonomous because it does not have any \( x \)'s explicitly present, which simplifies the analysis by allowing the equation to be treated as a function of \( y \) and \( y' \) alone.

💡Substitution

In the context of differential equations, substitution is a method used to simplify the equation by introducing a new variable. The script describes a substitution where \( Z = y' \), which transforms the second-order differential equation into a new form that is more manageable and reveals additional properties of the equation.

💡Chain Rule

The chain rule is a fundamental principle in calculus for differentiating composite functions. In the script, the chain rule is implicitly used when the instructor interprets the product \( 2ZZ' \) as the derivative of \( Z^2 \), which is a key step in simplifying the differential equation.

💡Separation of Variables

Separation of variables is a technique used to solve differential equations by rearranging the equation so that all terms involving one variable are on one side, and all terms involving the other variable are on the other side. The script uses this method to solve the equation \( 2Z' = Z^2 \) by isolating \( Z \) and \( X \) on opposite sides of the equation.

💡Anti-Derivative

An anti-derivative, or indefinite integral, is a function that, when differentiated, yields the original function. The script discusses finding anti-derivatives to solve for \( Z \) and \( y \) after separation of variables, which is a common approach in differential equations to find the function(s) that satisfy the equation.

💡ArcTan

ArcTan, or the inverse tangent function, is used to find the angle whose tangent is a given number. In the script, it appears in the context of solving the differential equation involving \( Z \) and \( a \), where \( \arctan(Z/a) \) is used to integrate and find the relationship between \( Z \) and \( X \).

💡Partial Fraction Decomposition

Partial fraction decomposition is a method used to integrate rational functions by breaking them into simpler fractions. The script mentions this technique in the context of integrating the equation \( \frac{1}{y^2 - a^2} \), which is a step towards finding the solution for \( y \).

💡Natural Logarithm

The natural logarithm, often denoted as \( \ln \), is the logarithm to the base \( e \) and is used in various mathematical and scientific contexts. In the script, the natural logarithm appears in the solution to the differential equation, where it is used to express the anti-derivative of certain terms.

💡Tangent

The tangent function is a trigonometric function that relates the angle of a right triangle to the ratio of the opposite side to the adjacent side. In the script, the tangent function is used to express \( y' \) in terms of \( x \) and a constant \( B \) after solving the differential equation.

💡Exponential Function

An exponential function is a function of the form \( e^x \), where \( e \) is the base of the natural logarithm. The script discusses exponential functions in the context of solving the differential equation, particularly when dealing with terms like \( e^{ax} \) and their integrals.

Highlights

Introduction of a nonlinear differential equation: y' = y' * y'.

Explanation of why the equation is nonlinear due to the quadratic term y' * y'.

Substitution introduced: setting Z = y' to simplify the equation.

Transformation of the original differential equation into a second-order differential equation.

Identification of the right-hand side as a product of a function and its derivative, implying the use of the chain rule.

Introduction of a constant 'a' to account for the possible addition of a constant in the solution.

Solution of the differential equation in the case where a = 0, using separation of variables.

Derivation of the solution for y in the case when a = 0, resulting in y being expressed as a logarithmic function.

Introduction of the case where a > 0, with the equation involving an arctan function.

Derivation of the solution for y when a > 0 and a plus sign in the equation, leading to a solution involving a natural logarithm of the secant function.

Introduction of the final case where a > 0 and a minus sign in the equation.

Application of partial fraction decomposition to solve the differential equation in the final case.

Derivation of the solution for y in the final case, involving the natural logarithm of a ratio of exponential functions.

Final simplification of the solution for y in the last case, resulting in a compact logarithmic expression.

Conclusion of the lecture with a well-structured and simplified final solution for y.

Transcripts

Browse More Related Video

Reducible Second Order Differential Equations, Missing Y (Differential Equations 26)

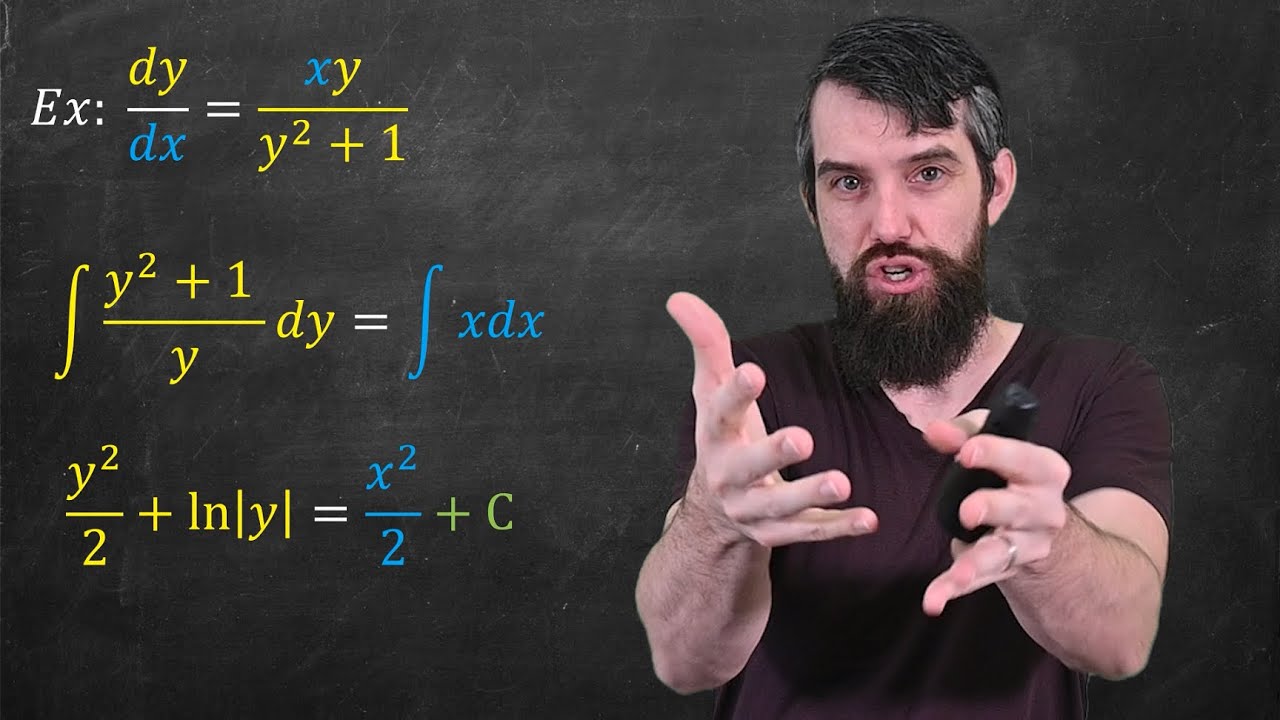
Separation of Variables // Differential Equations

Linear versus Nonlinear Differential Equations

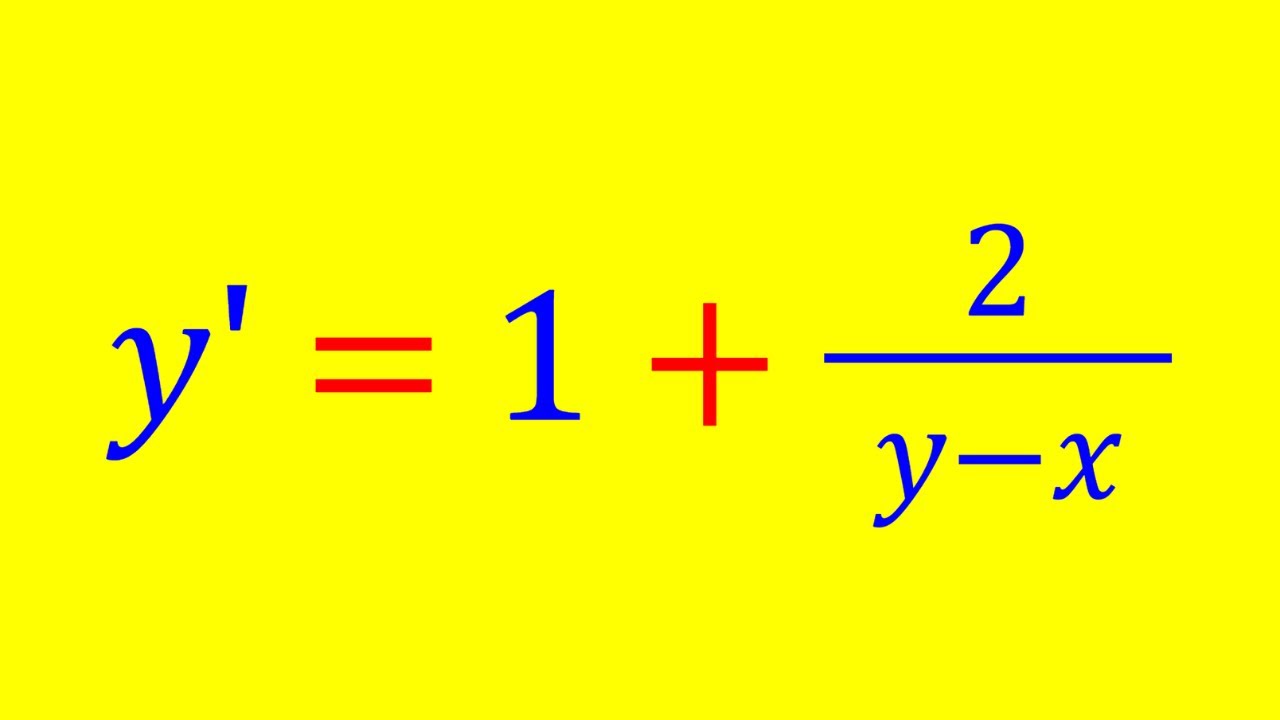
Solving A Non-Linear Differential Equation

AP Calculus AB Crash Course Day 5 - Integration and Differential Equations

Separable First Order Differential Equations - Basic Introduction

Related Tags

Differential Equations Nonlinear Dynamics Mathematics Educational Content Substitution Method Separation of Variables Autonomous Equation Chain Rule Integration Techniques Solving Equations Math Tutorial